Day 56 | 583. 两个字符串的删除操作 & 72. 编辑距离 & 编辑距离总结篇
583. 两个字符串的删除操作
解法一:直接求删除的步数
动态规划解题思路:
①确定dp数组以及下标含义
dp[i][j]:以下标i-1结尾的字符串s与下标j-1结尾的字符串t想要达到相等,所需要删除元素的最少次数。
②确定递推公式
每次遍历比较word1[i-1]与word2[j-1]的值。
若相等,则不删除元素:
dp[i][j]=dp[i-1][j-1]
若不相同,选择删除一个word1中元素或一个word2中的元素或同时删除word1和word2中的一个元素 三种情况下的最小值。
dp[i][j]=Math.min(dp[i-1][j-1]+2,Math.min(dp[i-1][j]+1,dp[i][j-1]+1));
③dp数组如何初始化
dp[i][0]代表word1和空字符串相等需要删除的最少步数,即把word1也变成空字符串,即为i
同理dp[0][j]=j;
④确定遍历顺序
从前向后、从上至下遍历。
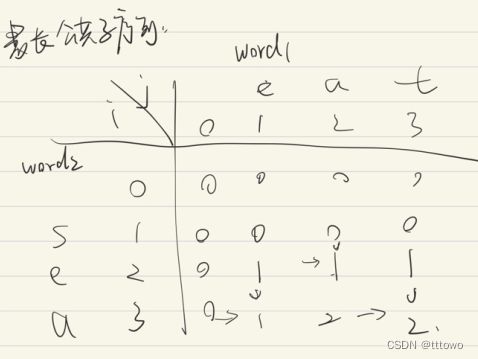
⑤举例推导dp数组
public int minDistance(String word1, String word2) {
int[][] dp=new int[word1.length()+1][word2.length()+1];
for(int i=0;i<=word1.length();i++){
dp[i][0]=i;
}
for(int j=0;j<=word2.length();j++){
dp[0][j]=j;
}
for(int i=1;i<=word1.length();i++){
for (int j=1;j<=word2.length();j++){
if(word1.charAt(i-1)==word2.charAt(j-1)){
dp[i][j]=dp[i-1][j-1];
}else{
dp[i][j]=Math.min(dp[i-1][j-1]+2,Math.min(dp[i-1][j]+1,dp[i][j-1]+1));
}
}
}
return dp[word1.length()][word2.length()];
}解法二:求出最长公共子序列长度,用字符串之和减去。
让 两个字符串的长度和-最长公共子序列的值*2也可求出本题答案。
动态规划解题思路:
①确定dp数组以及下标含义
dp[i][j]:长度为[0,i-1]的字符串s与长度为[0,j-1]的字符串t的最长公共子序列
②确定递推公式
每次遍历比较word1[i-1]与word2[j-1]的值。
若相等,则公共子序列长度+1:
dp[i][j]=dp[i-1][j-1]+1
若不相同,则为在word1/word2中去掉该元素的最长公共子序列值的较大值。
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])
③dp数组如何初始化
dp[i][0],dp[0][j]都为word1/word2与空字符串的最长公共子序列,即为0.
④确定遍历顺序
从前向后、从上至下遍历。
⑤举例推导dp数组
public int minDistance(String word1, String word2) {
int[][] dp=new int[word1.length()+1][word2.length()+1];
for(int i=1;i<=word1.length();i++){
for (int j=1;j<=word2.length();j++){
if(word1.charAt(i-1)==word2.charAt(j-1)){
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
return word1.length()+word2.length()-dp[word1.length()][word2.length()]*2;
}72. 编辑距离
这道题不太理解。。
动态规划解题思路:
①确定dp数组以及下标含义
dp[i][j]:下标为[0,i-1]的字符串1转换为下标为[0,j-1]的字符串2所需要的最少操作数
②确定递推公式
 每次遍历比较word1[i-1]与word2[j-1]的值。
每次遍历比较word1[i-1]与word2[j-1]的值。
(1) 若相等,则操作数不变:
dp[i][j]=dp[i-1][j-1]
(2)若不相同,则可进行三个操作:
①删除操作
word1删除下标i-1,即word1下标i-2与word2下标j-1的元素全部相等。即为dp[i-1][j]加一个操作
dp[i][j]=dp[i-1][j]+1
word2删除下标j-1,即word2下标j-2与word1下标i-1的元素全部相等。即为dp[i][j-1]加一个操作
dp[i][j]=dp[i][j-1]+1
②插入元素
与删除相同。
在word1插入说明word1下标i-2与word2下标j-1相同
在word2插入说明word1下标i-1与word2下标j-2相同
③替换元素
说明word1前i-2下标与word2前j-2下标相同,只需要把word1中的i-1下标替换成word2中的j-1下标
dp[i][j]=dp[i-1][j-1]+1;
最后,取三个的最小值即可。
dp[i][j]=Math.min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+1);
③dp数组如何初始化
dp[i][0],dp[0][j]都为word1/word2转换空字符串要进行的操作,即为字符串长度i/j个
dp[i][0]=i,dp[0][j]=j;
④确定遍历顺序
从前向后、从上至下遍历。
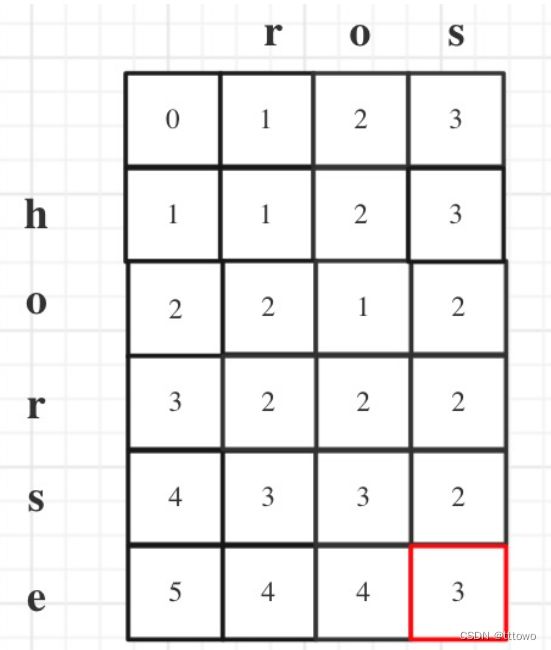
⑤举例推导dp数组
public int minDistance(String word1, String word2) {
int[][] dp=new int[word1.length()+1][word2.length()+1];
for(int i=0;i<=word1.length();i++){
dp[i][0]=i;
}
for(int j=0;j<=word2.length();j++){
dp[0][j]=j;
}
for(int i=1;i<=word1.length();i++){
for(int j=1;j<=word2.length();j++){
if(word1.charAt(i-1)==word2.charAt(j-1)){
dp[i][j]=dp[i-1][j-1];
}else{
dp[i][j]=Math.min(dp[i-1][j]+1,Math.min(dp[i][j-1]+1,dp[i-1][j-1]+1));
}
}
}
return dp[word1.length()][word2.length()];
}