R与结构方程模型(1):SEM的核心
R与结构方程模型
- 简介
- 图形模型
-
- 有向图(directed graphs)
-
- 1、标准回归模型
- 2、路径分析
-
- 2.1、关系类型
- 2.2、多个目标
- 2.3、间接效应
- 2.4、多中介模型
- 2.4、例子
- 间接效应的注意事项
- 术语问题
- 题外话1:工具变量(instrumental variable)
- Heckman 选择模型[^1]
- 题外:2:非递归模型
- 题外话3:跟踪原则
- 贝叶斯网络
- 无序图
- 总结
原文链接:Michael Clark电子书《Graphical&Latent Variable Modeling》
简介
lavaan包中定义的符号如下:
| 公式 | 操作 | 含义 |
|---|---|---|
| 定义潜变量 | =~ | 潜变量的测量的公式 |
| 回归 | ~ | |
| 协方差、方差 | ~~ | 相关性 |
| 截距 | ~1 | ~0为截距为0 |
| 固定参数 | _* | 固定某一个 |
| 命名 | abc* | 被命名为 |
MPlus的功能在R中对应的包
| model | package |
|---|---|
| 标准CFA、路径分析、SEM、增长模型(growth) | lavaan |
| 缺失值 | lavaan::FIML,semTools::MI+ |
| 多组分析 | lavaan, semTools |
| 固定效应模型 | flexmix, poLCA |
| Bayesian | blavaan |
| 因子评分回归 | lavvan |
| 可视化 | lavaanPlot |
图形模型
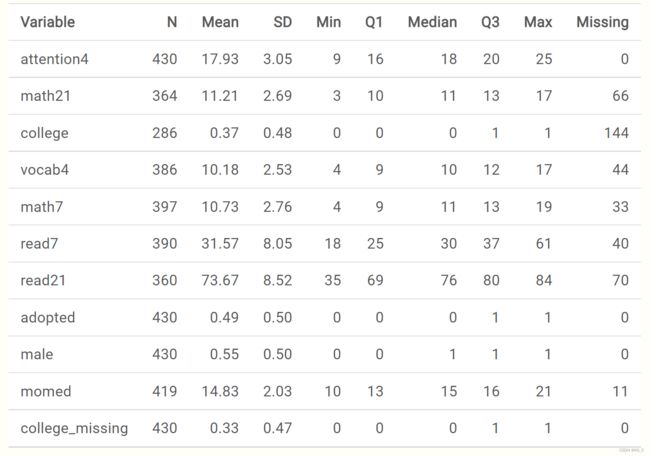
图形模型可以看作是通过边(或链接)连接节点(或顶点)的数学或统计构造。当看做统计模型时,节点表示我们数据集中感兴趣的变量,并且边代表它们之间的关系。他们看起来如下。

您执行的任何统计模型都可以表示为这样的图形模型。例如,第一个图形,具有 X、Y 和 Z 三个节点,表示 X 和 Z 预测 Y 的回归模型;中间的图表示间接效应,1、2、3图表示一个相关矩阵。
图形模型的一个关键思想是条件独立性,在构建模型时应该记住这一点。该概念可以通过下图进行演示。
在此图中,在给定 Y 的条件下,X 条件独立于 Z :一旦要去解释 Y (即 Y 做因变量时),那么 X 与 Z 之间是不相关的。在讨论路径分析和潜在变量模型时,我们将重新审视这个概念。图形可以是有向的、无向的或混合的。有向图有箭头,有时暗示因果流(很难明确证明)或注意时间分量(时序先后性)。无向图仅表示节点之间的关系,而混合图可能包含方向和对称关系。本文档中讨论的大多数模型都将是定向的或混合的。
有向图(directed graphs)
- 标准回归模型
- 路径分析
- 关系类型
- 多目标
- 间接效应
- 多调节
- 术语的问题
- 工具变量
- 非递归模型
- 跟踪原则
如前所述,我们可以将标准模型表示为图形模型。在大多数情况下,我们将处理有向图或混合图。我们几乎总是专门处理有向非循环图(即没有反馈循环的模型)。
1、标准回归模型
让我们从标准线性模型(SLM)开始,即我们可以通过普通最小二乘法(OLS,并非都是如此)估计的基本回归。在此设置中,我们要检查每个潜在预测变量(图中的 xn )对目标变量 (y) 的影响。下面显示了图形模型的外观。
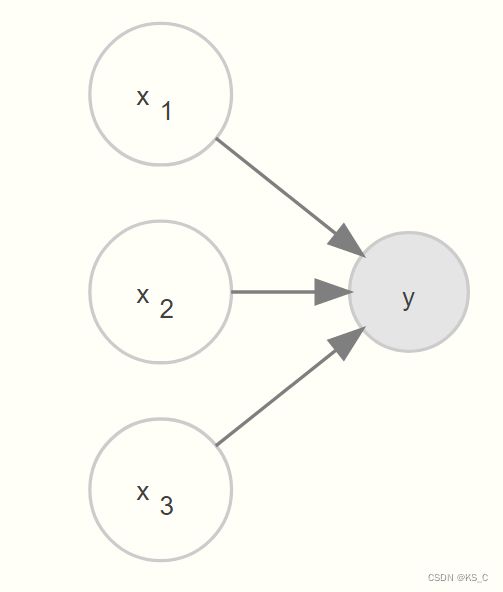
尽管看起来很简单,但是后续复杂模型中会用到相同的思维。我们将展示利用标准的R建模与用lavvan中sem建模的结果是否相同(尽管sem使用极大似然的方法,因此方差可能会有轻微不同。)。
首先利用lm进行建模
mcclelland = haven::read_dta('data/path_analysis_data.dta') #路径为存储该数据的路径
lmModel = lm(math21 ~ male + math7 + read7 + momed, data=mcclelland)
随后我们用lavaan包,虽然输入格式与结果会轻微不同(以SEM展示),但是参数完全相同。
library(lavaan) #载入lavaan包
model = "
math21 ~ male + math7 + read7 + momed #模型与lm建模完全一致
"
semModel = sem(model, data=mcclelland, meanstructure = TRUE)
summary(lmModel)
Call:
lm(formula = math21 ~ male + math7 + read7 + momed, data = mcclelland)
Residuals:
Min 1Q Median 3Q Max
-6.9801 -1.2571 0.1376 1.4544 5.7471
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.84310 1.16418 4.160 4.08e-05 ***
male 1.20609 0.25831 4.669 4.44e-06 ***
math7 0.31306 0.04749 6.592 1.76e-10 ***
read7 0.08176 0.01638 4.991 9.81e-07 ***
momed -0.01684 0.06651 -0.253 0.8
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.329 on 324 degrees of freedom
(101 observations deleted due to missingness)
Multiple R-squared: 0.258, Adjusted R-squared: 0.2488
F-statistic: 28.16 on 4 and 324 DF, p-value: < 2.2e-16
summary(semModel, rsq=T)
lavaan 0.6-2 ended normally after 21 iterations
Optimization method NLMINB
Number of free parameters 6
Used Total
Number of observations 329 430
Estimator ML
Model Fit Test Statistic 0.000
Degrees of freedom 0
Minimum Function Value 0.0000000000000
Parameter Estimates:
Information Expected
Information saturated (h1) model Structured
Standard Errors Standard
Regressions:
Estimate Std.Err z-value P(>|z|)
math21 ~
male 1.206 0.256 4.705 0.000
math7 0.313 0.047 6.642 0.000
read7 0.082 0.016 5.030 0.000
momed -0.017 0.066 -0.255 0.799
Intercepts:
Estimate Std.Err z-value P(>|z|)
.math21 4.843 1.155 4.192 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.math21 5.341 0.416 12.826 0.000
R-Square:
Estimate
math21 0.258
正如我们稍后将更详细地看到的那样,SEM包含更复杂的回归模型,但在这一点上,参数具有与我们的标准回归完全相同的理解,因为除了概念上之外,两个模型之间没有区别,因为SEM明确地为解释带来了因果关系。随着我们的前进,我们可以在统计上看到结构方程模型是我们已经非常熟悉的那些的推广,因此人们可以利用这些先验知识作为理解新知识的基础。
2、路径分析
路径分析实际上是一种非常古老的技术,可以看做是标准线性回归(SLM)的一种推广。可以允许间接效应和多个目标变量。
2.1、关系类型
大多数模型只处理直接效应。在这种情况下,我们不希望考虑干预变量。如确实存在干预变量(例如图中的B),那么我们所处理的是通常称为中介模型的东西,并且必须报告间接和(潜在的)直接影响。
在处理多个结果时,有些结果可能具有共同的预测因子,因此结果的相关性可以通过这些共同诱因来解释(这将在稍后的因子分析中出现)。通常存在未分析的相关。例如,每次运行回归时,预测变量之间的相关性都是“未分析”。

2.2、多个目标
虽然相对较少使用,但多变量线性回归(多个因变量)实际上在某些编程环境(如R)中非常简单,并且执行具有多变量结果的模型不需要任何特定于SEM的内容,但这是我们将坚持的领域。
使用McClelland的数据,让我们自己尝试一下。首先,让我们看一下数据的大体情况。
虽然一开始这些变量之间相关很弱,但一个合理的模型可能能够预测21岁时的数学和阅读,并在前几年采取措施。
model = "
read21 ~ attention4 + vocab4 + read7
math21 ~ attention4 + math7
read21 ~~ 0*math21 #~~代表相关改代码表示read21和math21是相互独立的。
"
mvregModel = sem(model, data=mcclelland, missing='listwise', meanstructure = T)
coef(mvregModel)
read21~attention4 read21~vocab4 read21~read7 math21~attention4 math21~math7 read21~~read21
0.128 0.377 0.537 0.091 0.347 51.837
math21~~math21 read21~1 math21~1
5.965 50.290 5.856
模型代码的最后一行阐明了我们将math21和read21视为独立的,因此我们只是同时运行两个单独的回归。
另请注意,输出中有**~1**的系数是截距。
我们可以将其与标准R回归进行比较。第一步使数据等于lavan中使用的数据。为此,我们可以使用 dplyr 包为模型选择必要的变量,然后省略缺少的个案。
library(dplyr)
mcclellandComplete = select(mcclelland,
read21, math21, attention4, vocab4, read7, math7) %>% na.omit
lm(read21 ~ attention4 + vocab4 + read7, data=mcclellandComplete)
Call:
lm(formula = read21 ~ attention4 + vocab4 + read7, data = mcclellandComplete)
###
Coefficients:
(Intercept) attention4 vocab4 read7
50.2904 0.1275 0.3770 0.5368
###
lm(math21 ~ attention4 + math7, data=mcclellandComplete)
###
Call:
lm(formula = math21 ~ attention4 + math7, data = mcclellandComplete)
Coefficients:
(Intercept) attention4 math7
5.85633 0.09103 0.34732
###
其中使用sem函数估算模型read21 ~ attention4 + vocab4 + read7得到的参数分别为:
read21 ~ attention = 40.128
read21 ~ vocab4 = 0.377
read21 ~ read7 = 0.537
read21 ~ 1 = 50.290
使用sem函数估算模型math21 ~ attention4 + math7得到的参数分别为
math21 ~ attention4 = 0.091
math21 ~ math7 = 0.347
math21 ~ 1 = 5.856
math21 ~ ~ math21表示math的方差为5.965 ;read21 ~ ~ read21表示read21的方差为51.837
可以看见用sem函数估算的参数值和lm函数的参数完全相同。
删除math21和read21之间不相关(math21 ~ 0*read21)的约束,这是可以计算得到二者的协方差。而此时得到的参数与lm函数的结果不同。read21~~math21表示read与math21之间的协方差。
model = "
read21 ~ attention4 + vocab4 + read7
math21 ~ attention4 + math7
"
mvregModel = sem(model, data=mcclelland, missing='listwise', meanstructure = T)
coef(mvregModel