B站左程云算法视频笔记05

两个链表相交的一系列问题

题目：给定两个可能有环也可能无环的单链表，头结点head1和head2，请实现一个函数，如何两个链表相交，请返回相交的第一个节点，如果不相交，返回null

要求：如果两个链表长度之和为N，时间复杂度要在O(N)，额外空间复杂度O(1)

分析：1.判断有无环2.判断的是两个链表中是否有节点的内存地址一样，和值无关

第一步：判断有无环，有环返回第一个入环节点。分为哈希表和快慢指针的做法可实现

第二步：讨论，获知了两个链表是否有环，分情况讨论。都无环，可能相交也可能不相交，讨论两个链表的尾节点的地址是否一致，不是，则不相交，一致，则让长链表先走两个链表长度的插值步之后，再一起走，会在第一个相交节点相遇；一个有环，一个无环，不相交，返回null；都有环，分为三种情况，不相交，相交且入环节点一样，相交但入环节点不一样。

都有环的三种情况区分较复杂，首先判断判断入环节点一样时，则链表1和链表2 的入环节点的内存结点相等，此时，我们可以把入环节点看作是终止节点，则将问题转换成了都无环时候的情况；入环节点不一样时，给一个指针指向链表1的入环节点，继续往下走，在遇到自己之前，遇到了2的入环节点，则返回1或2的入环节点，如果没遇到，则说明不相交，返回null。

代码：

//找到第一个入环节点，如果无环，则返回空
public static Node getLoopNode(Node head){
    if(head == null || head.next == null || head.next.next == null){
            return null;
    }
    Node n1 = head.next; //n1 -> slow
    Node n2 = head.next.next;//n2 -> fast
    while( n1 != n2 ){
        if(n2.next ==null || n2.next.next == null){
            return null;
        }
        n2 = n2.next.next;
        n1 = n1.next;
    } 
    n2 = head; // n2-> walk again from head
    while(n1 != n2){
        n1 = n1.next;
        n2 = n2.next;
    }
    return n1;
}

//如果两个链表都无环，返回第一个相交节点，如果不相交则返回空
public static Node noLoop(Node head1, Node head2){
    if(head1 == null || head2 == null){
        return null;
    }
    Node cur1 = head1;
    Node cur2 = head2;
    int n = 0;//两个链表的长度差值
    while(cur1.next != null){//到最后一个节点停
        n++;
        cur1 = cur1.next;
}//得到链表1的最后一个节点
    while(cur2.next != null){
        n--;
        cur2 = cur2.next;
}//链表2的最后一个节点
    if(cur1 != cur2){
        return null;
}最后一个链表不等，则不相交
cur1 = n > 0? head1:head2; //cur1指向长的链表的头结点
cur2 = cur1==head1? head2:head1;//cur2指向短的
n= Math.abs(n); n取绝对值
while(n != 0){
    n--;
    cur1 = cur.next;
}//长的先走
while(cur1 != cur2){
    cur1 = cur1.next;
    cur2 = cur2.next;
}
    return cur1;
}

//两个有环链表，返回第一个相交节点，不相交返回null
public static Node bothLoop(Node head1, Node loop1, Node head2, Node loop2){
        Node cur1 = null;
        Node cur2 = null;
        if(loop1 == loop 2){
            cur1 = head1;
            cur2 = head2;
            int n = 0;
            while(cur1 != loop1){
            n++;
            cur1 = cur1.next;
    }
            while(cur2 != loop2){
            n--;
            cur2 = cur2.next;
}
        cur1 = n>0? head1:head2;
        cur2 = cur1 == head1? head2:head1;
        n =Math.abs(n);
        while(n != 0){
           n--;  
        cur1 = cur1.next;  
}
        while(cur1 != cur2){
        cur1 = cur1.next;
        cur2 = cur2.next;
}
        return cur1;
    }else{
        cur1 = loop1.next;
        while(cur1 != loop1){
          if(cur1 == loop2){
            return loop1;
    }
        cur1 = cur1.next;
}
        return null;

}

}

public statci Node getIntersectNode(Node head1, Node head2){
        if(head1 == null || head2 == null){
            return null;
}
        Node loop1 = getLoopNode(head1);
        Node loop2 = getLoopNode(head2);
        if(loop1 == null && loop2 =null){
            return noLoop(head1, head2);
}
        if(loop1 !=null && loop2 != null){
            return bothLoop(head1, loop1, head2, loop2);
}
        return null;
}

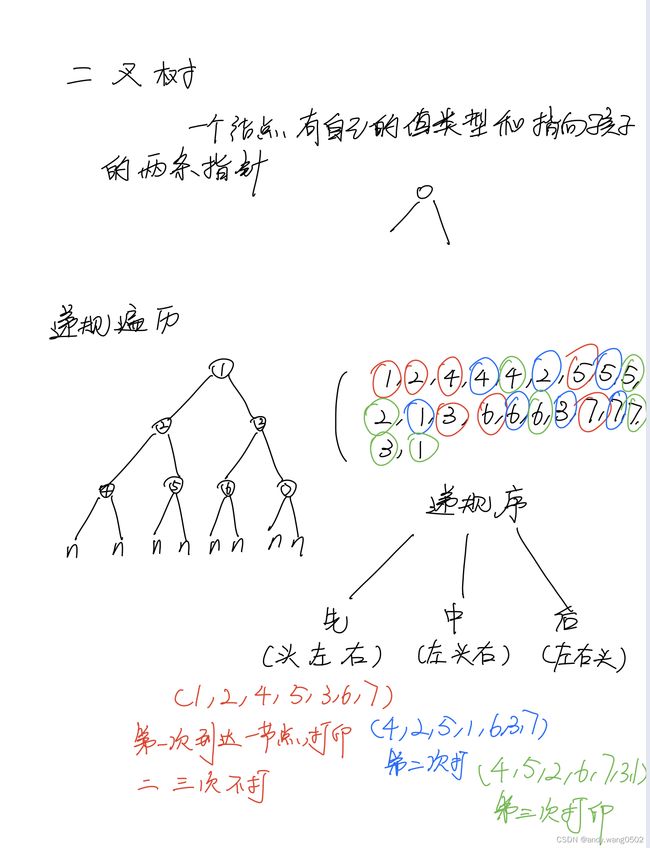
二叉树节点结构

递归行为三次达到自己

public static void f(Node head){
    //1
    if(head == null){
        return;
}
//1
f(head.left);
//2
f(head.right);
//3
}

public static preOrderRecur(Node head){
if(head == null){
    return;
}
System.out.print(head.value+"");//第一次打印是先序
preOrderRecur(head.left);
preOrderRecur(head.left);
}


public static inOrderRecur(Node head){
if(head == null){
    return;
}
inOrderRecur(head.left);
System.out.print(head.value+"");//第二次打印是中序
inOrderRecur(head.left);
}


public static posOrderRecur(Node head){
if(head == null){
    return;
}
posOrderRecur(head.left);
posOrderRecur(head.left);
System.out.print(head.value+"");//第三次打印是后序
}

 任何递归函数都可改成非递归

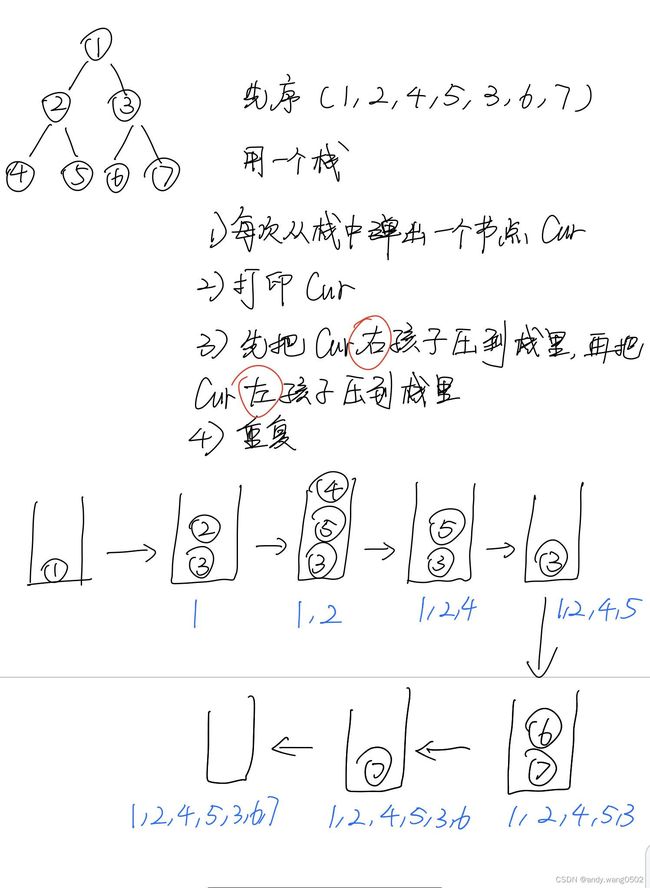
public static void preOrderUnRecur(Node head){
System.out.print("pre-order:  ");
if(head ! = null){
    Stack stack = new Stack();
    stack.add(head);
    while(!stack.isEmpty()){
        head = stack.pop();//弹出
        System.out.print(heaf.value+" ");
        if (head.right != null){
            stack.push(head.right);
}
        if(head.left != null){
            stack.push(head.left);
}
}
}
    System.out.println();

}

 

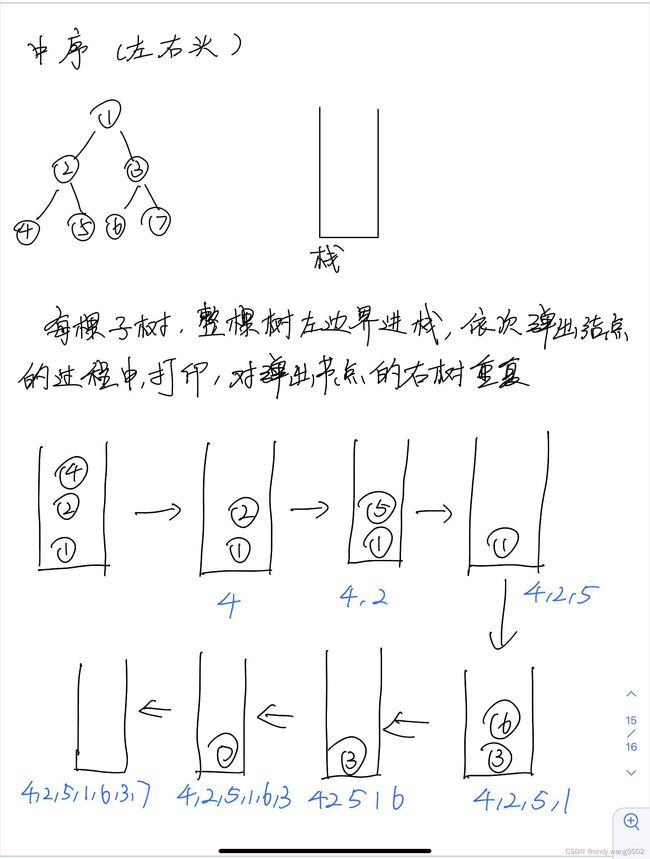
public static void inOrderUnRecur(Node head){
    System.out.print("in-order: ");
    if(head != null){
        Stack stack = new Stack();
        while(!stack.isEmpty() || head! == null){
            if(head != null){
            stack.push(head);
            head = head.left;
        }else{
            head = stack.pop;
            System.out.print(head.value+" ");
            head = head.right;
}
}
}
        System.out.println();
}

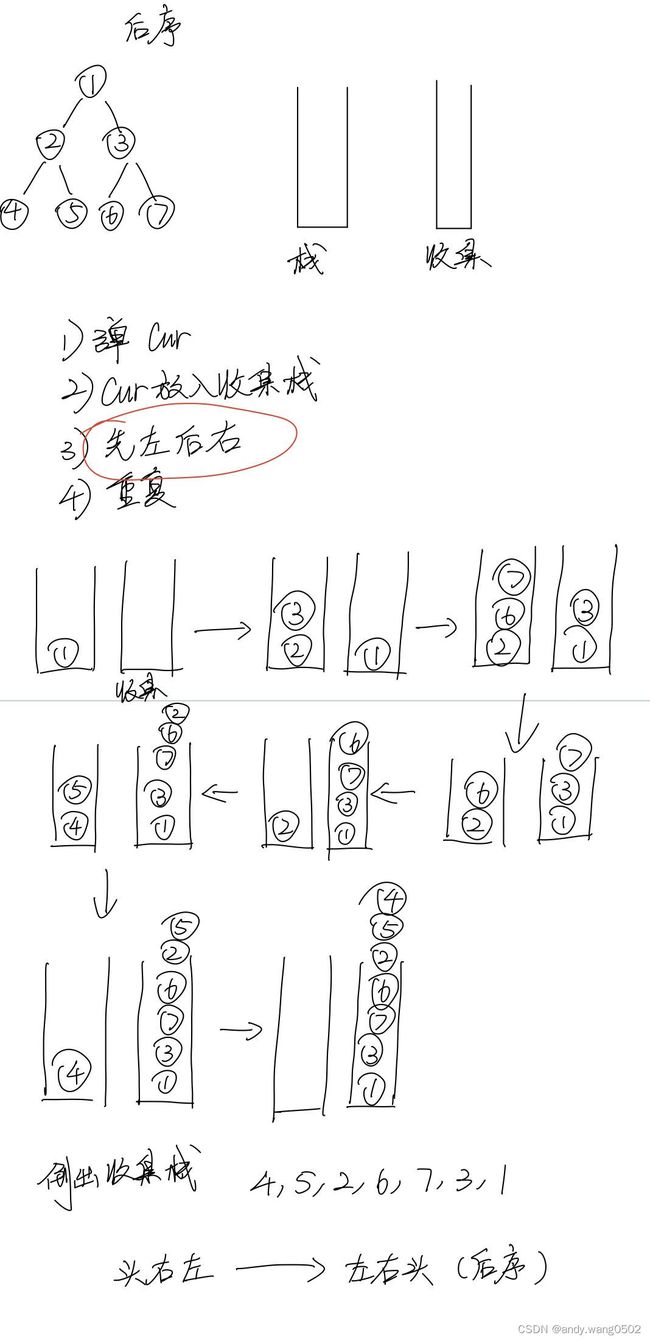
public static void posOrderUnRecur(Node head){
System.out.print("pos-order:  ");
if(head ! = null){
    Stack s1 = new Stack();
    Stack s2 = new Stack();//收集
    s1.push(head);
    while(!s1.isEmpty()){
        head = s1.pop();//弹出
        s2.push(head);
        if(head.left != null){
            s1.push(head.left);
}
        if (head.right != null){
            s1.push(head.right);
}
        
}
    while(!s2.isEmpty()){
        System.out.print(s2.pop.value+"")
}
}
    System.out.println();

}


​

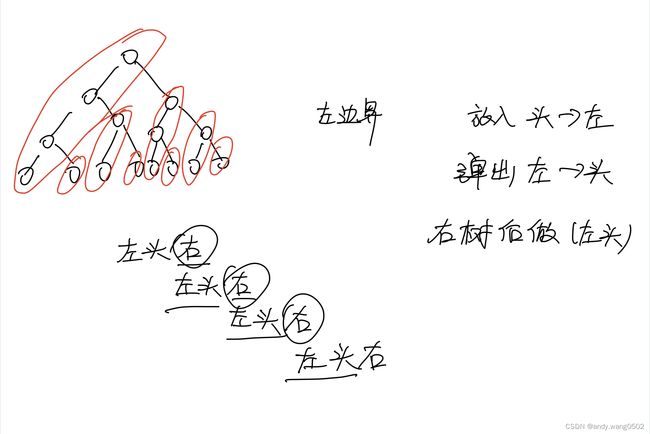
所有的树都可以被左边界分解掉

 设计题：如何完成二叉树的宽度优先遍历（求一棵二叉树的宽度）LeetCode662和102 《剑指offer》32

队列，先放左再放右

宽度优先遍历

public static int void w(Node node){
     if(head == null){
        return;
}
    Queue queue = new LinkedList<>();
    queue.add(head);
    while(!queue.isEmpty()){
        Node cur = queue.poll();
        System.out.println(cur.value);//弹出就打印
        //先放左再放右边
        if(cur.left != null){
            queue.add(cur.left);
}
        if(cur.right != null){
            queue.add(cur.right);
}
}
}

求出最大宽度

思路：准备一个levelMap记录点在第几层，设置三变量，当前在哪一层curLevel，当前层发现几个节点curLevelNodes，所有层中哪一层发现的节点最多的max

public static int void w(Node node){
     if(head == null){
        return;
}
    Queue queue = new LinkedList<>();
    queue.add(head);
    HashMap levelMap = new HashMap<>();//记录每个节点对应的层数
    levelMap.put(head,1);//放入第一个节点
    int curLevel = 1;//当前节点所在的层数
    int curLevelNodes = 0;//当前层发现几个节点数
    int max = Integer.Min_VALUE;//哪一层发现的最多的节点数
    while(!queue.isEmpty()){
        Node cur = queue.poll();
        int curNodeLevel = levelMap.get(cur);//节点的层数
        if(curNodeLebel == curLevel){//节点是否是当前统计的层
            curLevelNodes++;
}else{
        max = Math.max(max,curLevelNodes);
        curLevel++;
        curLevelNodes=1;
}
        //先放左再放右边，记录每个点所在的层数
        if(cur.left != null){
            levelMap.put(cur.left, curNodeLevel+1);
            queue.add(cur.left);
}
        if(cur.right != null){
            levelMap.put(cur.right, curNodeLevel+1);
            queue.add(cur.right);
}
        
}
}

不用哈希表的方法

使用队列，变量，当前层最后一个节点curend，下一层最后一个节点nextend，当前层已经发现的节点数curlevelNode，谁进栈，谁就是nextend，当出队列的节点是curend时，max抓取记录的curlevelNode。