二叉树的非递归遍历算法
二叉树的非递归遍历算法
二叉树的遍历是指访问二叉树的每个结点,且每个结点仅被访问一次。二叉树的遍历可按二叉树的构成以及访问结点的顺序分为4种方式:先序遍历、中序遍历、后序遍历和层次遍历。请至少给出其中一种遍历方式的非递归算法的思路和代码,并举例演示算法的执行过程。
先序遍历
算法思路:采用栈来实现先序遍历的非递归算法。创建栈,并初始化。遍历结点,若结点存在,则入栈,并输出结点的值,指向其左孩子;否则出栈,访问结点,指向其右孩子。如果结点不存在或者栈为空,则遍历结束。
代码:
//先序遍历二叉树
void PreOrder(BiTree T)
{
SqStack* S;
S = InitStack();
BiTreeNode* p;
p = T;
while (p|| !StackEmpty(*S))
{
if (p)
{
printf("%c",p->data);
Push(S, p);
p = p->LChild;
}
else
{
Pop(S, &p);
p = p->RChild;
}
}
}
演示过程(以先序遍历输入ABD##E##CF###为例)
此时输出:A
此时输出:AB
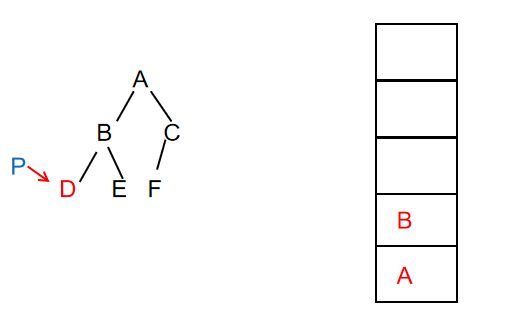
此时输出:ABD
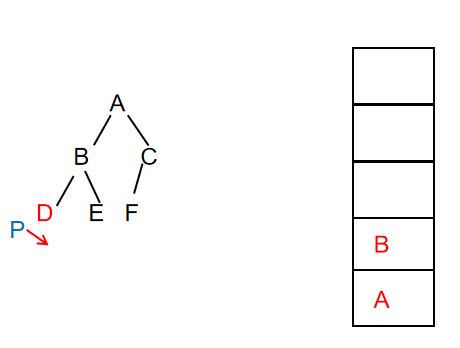
此时输出:ABD(不变)
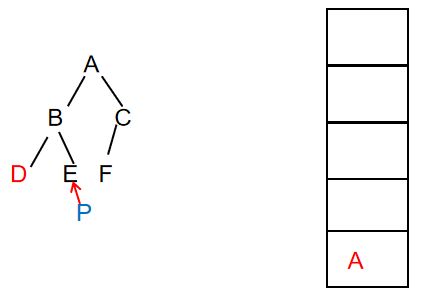
此时输出:ABD(不变)
此时输出:ABDE
此时输出:ABDE(不变)
此时输出:ABDE(不变)
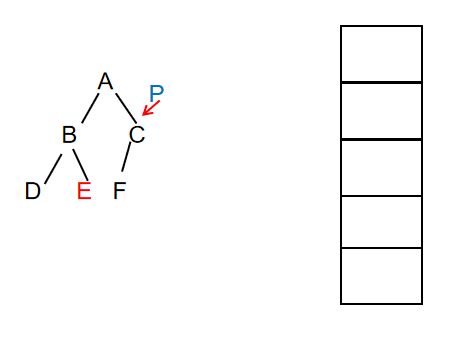
此时输出:ABDEC
此时输出:ABDECF
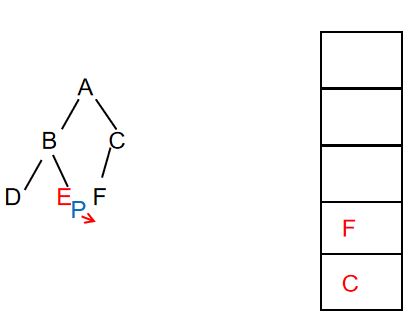
- 继续遍历结点,此时F结点的左孩子为空,则将栈顶元素F出栈,P指向F结点的右孩子
此时F结点的右孩子也为空,继续将栈顶元素C出栈,P指向C结点的右孩子,此时P指向的结点为空,栈也为空,遍历结束。
中序遍历
算法思路:同样也是用栈,与先序遍历相同,只是输出在不同位置。创建栈,并初始化。遍历结点,若结点存在,则入栈,指向其左孩子;否则出栈,访问结点,并输出结点的值,指向其右孩子。如果结点不存在或者栈为空,则遍历结束
代码:
//中序遍历二叉树
void InOrder(BiTree T)
{
SqStack* S;
S = InitStack();
BiTreeNode* p;
p = T;
while (p || !StackEmpty(*S))
{
if (p)
{
Push(S, p);
p = p->LChild;
}
else
{
Pop(S, &p);
printf("%c", p->data);
p = p->RChild;
}
}
}
后序遍历
算法思路:由于后序遍历是后序遍历根节点的左子树,后序遍历根节点的右子树,最后访问根节点,那么最大问题就是判断是否该结点结束遍历左子树,所以采取以下操作来解决。同样也使用一个栈,初始化栈,遍历结点,若结点存在,结点入栈,并对该结点标志位0,表示该结点尚未被遍历其左子树,然后指向其右结点;若结点不存在,满足该结点的左子树已被遍历进入循环,遍历该结点的右子树。不满足退出循环,然后继续出栈得到子结点,并将其压入栈,指向子节点的右孩子,并对该结点标志为1。
代码:
//后序遍历
void Postorder(BiTree T)
{
SqStack* S;
S = InitStack();
BiTreeNode* p;
p = T;
char tag[Maxsize] = {'0'};
while (p || !StackEmpty(*S))
{
if (p)
{
Push(S, p);
tag[S->top] = '0';//标志结点是否遍历右子树
p = p->LChild;
}
else
{
while (tag[S->top] == '1') {
Pop(S, &p);
printf("%c",p->data);
}
if (S->top == -1) break;
Pop(S, &p);
Push(S, p);
p = p->RChild;
tag[S->top] = '1';
}
}
}
层次遍历
算法思路:采用顺序队列来实现,将根节点入队,进入循环,将队头指针所指的元素出队,并输出其结点的值,如果该结点的左孩子存在,将其左孩子入队,如果该结点的右孩子存在,将右孩子入队,直到队头指针和队尾指针相等退出循环。
代码:
//层次遍历
void Levelorder(BiTree T)
{
BiTree Q[Maxsize];
int front, rear;
if (T == NULL)return;
front = -1;
rear = 0;
Q[rear] = T;
while (front != rear)
{
front++;
printf("%c",Q[front]->data);
if (Q[front]->LChild != NULL)
{
rear++;
Q[rear] = Q[front]->LChild;
}
if (Q[front]->RChild != NULL)
{
rear++;
Q[rear] = Q[front]->RChild;
}
}
}
代码汇总
//非递归先序遍历、中序遍历、后序遍历可用栈来实现
//层次遍历可用队列来实现
//作者:Second to none
#include