详解分治算法
详解分治算法
文章目录
- 详解分治算法
-
- 概念
- 适用条件
- 解题步骤
- summary
-
- 时间复杂度
- 分治法-动态规划联系
-
- 相同点
- 不同点
- 基于分治算法的一些「有名」算法
-
- 快排和归并排序
- 归并排序的应用
-
- 数组中的逆序对
- 右侧更小的元素个数
- summary
- Top k 问题-randomized select
-
- 两个有序数组的 topk 问题
- 汉诺(Hanoi)塔问题
-
- 引入
- 思路分析
-
- 时间复杂度
- 例题
-
- leetcode-241-为运算表达式设计优先级
- leetcode-53-最大子序和
-
- Kadane algorithm
- leetcode-169-多数元素
- leetcode-932-漂亮数组
-
- summary
- leetcode-190-Reverse Bits
-
- >>> 同类型 leetcode-191-hammingWeight
- leetcode-395-Longest Substring with At Least K Repeating Characters
references:
分治算法详解
分治算法总结
概念
字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)……
分治策略是:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。
如果原问题可分割成k个子问题,1
适用条件
- 该问题的规模缩小到一定的程度就可以容易地解决
- 该问题可以分解为若干个规模较小的相同问题。(该条件反映了递归思想的存在,但不一定是最优子结构)
- 利用该问题分解出的子问题的解可以合并为该问题的解;
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子子问题。
备注:
-
3)是关键,能否利用分治法完全取决于问题是否具有第三条特征,如果具备了第一条和第二条特征,而不具备第三条特征,则可以考虑用贪心法或动态规划法。
-
4)涉及到分治法的效率,如果各子问题是不独立的则分治法要做许多不必要的工作,重复地解公共的子问题,此时虽然可用分治法,但一般用动态规划法较好。
解题步骤
- 分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题;
- 解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题
- 合并:将各个子问题的解合并为原问题的解。通常此步骤的时间复杂度为 O(N),可以以这个为背景反推合并的方式。
一般算法设计模式如下:
Divide-and-Conquer(P)
1. if |P|≤n0
2. then return(ADHOC(P))
3. 将P分解为较小的子问题 P1 ,P2 ,...,Pk
4. for i←1 to k
5. do yi ← Divide-and-Conquer(Pi) △ 递归解决Pi
6. T ← MERGE(y1,y2,...,yk) △ 合并子问题
7. return(T)
|P|表示问题P的规模;n0为一阈值,表示当问题P的规模不超过n0时,问题已容易直接解出,不必再继续分解。ADHOC(P)是该分治法中的基本子算法,用于直接解小规模的问题P。因此,当P的规模不超过n0时直接用算法ADHOC(P)求解。- 算法
MERGE(y1,y2,...,yk)是该分治法中的合并子算法,用于将P的子问题P1 ,P2 ,…,Pk的相应的解y1,y2,…,yk合并为P的解。
summary
时间复杂度
其中C(n)是合并(combine),D(n)是分解(divide)所需的时间复杂度
一般这种情况根据master theorem即可得到答案,具体可以参看我在进入搜索「主定理」中做的总结
分治法-动态规划联系
references:
动态规划和分治法的区别
递归,分治算法,动态规划和贪心选择的区别
相同点
- 大问题可以分解为若干个子问题
- 子问题更容易求解
====> 动态规划是分治+解决子问题冗余
不同点
个人的一点看法,在很多博客中都讲到分治是自顶向下,dp是自底而上,当然这种说法没有什么大毛病,但容易误导初学者,在看到下面这张图中的分治是先选择再解决子问题,dp是先解决子问题再选择之后才更容易让人理解
基于分治算法的一些「有名」算法
快排和归并排序
详情参考我的另一篇总结:javascript排序算法
- 快速排序
- 归并排序
Python 版本请看 github repo
def quick_sort(nums: List[int], start: int, end: int):
"""
尝试一下原地快排,此时时间复杂度最好为 O(NlogN) 最差的情况下基准值正好是最大或最小值,则为 O(N^2)
空间复杂度为递归调用栈占用的空间为:O(logN)
:param end:
:param start:
:param nums:
:return:
"""
def partition(nums: List[int], start: int, end: int) -> int:
"""
将 nums[end] 作为 pivot,此时所有元素都在其左边,只需要找到比它大的值放到它右边去即可
4 6 5 1 3
i = 4 j =4
i=4 j=3
i=4 j=2
i=3 j=2
4 6 1 5 3
i=3 j=1
i=2 j=1
4 1 6 5 3
i=2 j=0
i=1 j=0
1 4 6 5 3
:param nums:
:param start:
:param end:
:return:
"""
pivot, i = nums[end], end
# 此时不能正序来,因为最终会把 i j 全都交换成最初的样子,要让 i 始终大于等于 j
for j in range(end, start-1, -1):
if nums[j] > pivot:
i -= 1
nums[i], nums[j] = nums[j], nums[i]
nums[end], nums[i] = nums[i], nums[end]
return i
def partition_1(nums: List[int], start: int, end: int) -> int:
"""
把小于 pivot 的值向左放,最后把 pivot 放在它该在的位置上
:param nums:
:param start:
:param end:
:return:
"""
pivot, i = nums[start], start
# 要让 i 始终小于等于 j
for j in range(start, end + 1):
if nums[j] < pivot:
i += 1
nums[i], nums[j] = nums[j], nums[i]
nums[start], nums[i] = nums[i], nums[start]
return i
if start > end:
return
pivot = partition(nums, start, end)
quick_sort(nums, start, pivot - 1)
quick_sort(nums, pivot + 1, end)
def merge_sort(nums: List[int], start: int, end: int) -> List[int]:
"""
归并排序的关键在于将数组分成两部分,分别排序,然后将两个有序的数组合并,即得到一个有序的数组
时间复杂度:F(n) = 2F(n/2)+n 根据主定理,时间复杂度为 O(NlogN)
空间复杂度:O(N) logN 是递归调用栈的空间,N 是辅助数组占用的空间,总体是 O(N)
:param end:
:param start:
:param nums:
:return:
"""
if start >= end:
return
def merge(nums: List[int], start: int, mid: int, end: int):
"""
start~mid 有序
mid+1~end 有序
将 nums start~end 变成有序的
2 5 7
1 2 6
1 2 7
5 2 6
:param nums:
:param start:
:param mid:
:param end:
:return:
"""
res = []
i = start
j = mid + 1
while i <= mid or j <= end:
if i > mid and j <= end:
res.append(nums[j])
j += 1
elif i <= mid and j > end:
res.append(nums[i])
i += 1
elif nums[i] > nums[j]:
res.append(nums[j])
j += 1
else:
res.append(nums[i])
i += 1
for i in range(start, end + 1):
nums[i] = res[i - start]
mid = (start+end) // 2
merge_sort(nums, start, mid)
merge_sort(nums, mid + 1, end)
merge(nums, start, mid, end)
归并排序的应用
归并排序使用了分治的思想,通常我们在遇到暴力使用嵌套循环解决问题时会想到使用双指针优化方案,但由于无法知道窗口限制条件等因素无法使用滑动窗口,此时可以考虑分治解决
数组中的逆序对
class Solution:
def reversePairs_0(self, nums: List[int]) -> int:
"""
暴力法:双层循环,固定一个数遍历另一个数,这种场景通常考虑双指针优化,比如滑动窗口,但由于没有限制所有无法使用
时间复杂度:O(N^2)
空间复杂度:O(1)
:param nums:
:return:
"""
length = len(nums)
res = 0
for i in range(length):
for j in range(i + 1, length):
if nums[i] > nums[j]:
res += 1
return res
def reversePairs(self, nums: List[int]) -> int:
"""
当找不到更好的解决方法时可以考虑分治法,我们可以先找到左侧符合条件的+右侧符合条件的,假如左右有序,则可以在 O(N) 时间范围内找到两者
结合符合条件的,此时则找到了答案,其实以上我们应用了归并排序的思想
时间复杂度: O(NlogN) T(n) = 2T(n/2) + n
空间复杂度:O(N) 主要是合并排序的时候用到的空间
:param nums:
:return:
"""
length = len(nums)
def merge(start: int, mid: int, end: int) -> int:
"""
合并的时间复杂度为 O(2N) 即 O(N)
:param start:
:param mid:
:param end:
:return:
"""
i, m = start, start
j, n = mid + 1, mid + 1
res = []
count = 0
# 1 3 4
# 1 2 2
while m <= mid:
while n <= end and nums[n] < nums[m]:
n += 1
count += n - (mid+1)
m += 1
while i <= mid or j <= end:
if i <= mid and j <= end:
if nums[i] > nums[j]:
res.append(nums[j])
j += 1
else:
res.append(nums[i])
i += 1
elif i <= mid:
res.append(nums[i])
i += 1
elif j <= end:
res.append(nums[j])
j += 1
nums[start:end+1] = res
return count
def reverse(start: int, end: int) -> int:
if end <= start:
return 0
mid = (start + end) // 2
left_res = reverse(start, mid)
right_res = reverse(mid + 1, end)
merge_res = merge(start, mid, end)
return left_res + right_res + merge_res
return reverse(0, length - 1)
友情链接 >>>
493. Reverse Pairs
327. Count of Range Sum
右侧更小的元素个数
class Solution:
def countSmaller_0(self, nums: List[int]) -> List[int]:
"""
使用 SortedList 它插入元素的复杂度是 logN 使用 bisect_left 可以找到目标元素可以插入的最左侧的位置,也就是大于等于该元素的第一个
值所在的位置
时间复杂度:O(NlogN)
空间复杂度:O(N)
:param nums:
:return:
"""
from sortedcontainers import SortedList
length = len(nums)
res = [0] * length
sl = SortedList([nums[-1]])
for i in range(length - 2, -1, -1):
idx = sl.bisect_left(nums[i])
res[i] = idx
sl.add(nums[i])
return res
def countSmaller(self, nums: List[int]) -> List[int]:
"""
结合 reversePairs 的做法,这题也可以使用分治法来解决,重点也是归并排序,但问题在于怎么将值归总到每个元素所在位置上,所以我们需要
冗余一个索引位进来,参考下文
时间复杂度:O(NlogN)
空间复杂度:O(N)
:param nums:
:return:
"""
length = len(nums)
for i in range(length):
nums[i] = (i, nums[i])
res = [0] * length
def merge(start: int, mid: int, end: int):
i, m = start, start
j, n = mid + 1, mid + 1
tmp_res = []
while m <= mid:
while n <= end and nums[n][1] < nums[m][1]:
n += 1
res[nums[m][0]] += n-(mid+1)
m += 1
while i <= mid or j <= end:
if i <= mid and j <= end:
if nums[i][1] > nums[j][1]:
tmp_res.append(nums[j])
j += 1
else:
tmp_res.append(nums[i])
i += 1
elif i <= mid:
tmp_res.append(nums[i])
i += 1
elif j <= end:
tmp_res.append(nums[j])
j += 1
nums[start:end + 1] = tmp_res
def count(start: int, end: int):
if end <= start:
return
mid = (start + end) // 2
count(start, mid)
count(mid + 1, end)
merge(start, mid, end)
return
count(0, length - 1)
return res
summary
- 嵌套循环无法用双指针优化时可以考虑分治法,尤其比大小的问题,可以用有序数组来解决
- 上述几题都应用到了两个有序数组使用双指针的场景,最差是使用暴力法,此时时间复杂度为 O(MN),但其实我们在嵌套循环的过程中会发现有些值重复计算了,所以可以利用双指针将其优化到 O(M+N),参考详解双指针法
Top k 问题-randomized select
TopK问题三种方法总结
参考算法导论 9.2 期望为线性时间的选择算法:以快排为基础,随机选择 pivot 寻找其真正所在的位置,如果 pivot 正好为要找的值则返回,否则根据它跟 k 的关系仅递归一侧。
Randomized-select 其实是一种随机算法,最坏情况下的时间复杂度为 O ( N 2 ) O(N^2) O(N2),每次划分时极可能选择的基准值就是余下元素的最大或最小值。根据书中的证明:假设所有元素都是互异的,在期望线性时间内可以通过该算法找到任一顺序统计量,特别是中位数。
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
"""
:param nums:
:param k:
:return:
"""
def choose(start: int, end: int, target: int) -> int:
"""
:param start: 开始索引
:param end: 结束索引
:param target: 希望大于 pivot 的数的量,求 topk 问题时,初次递归的 target 即为 k-1
:return:
"""
def swap(i: int, j: int):
nums[i], nums[j] = nums[j], nums[i]
def partition(start: int, end: int) -> int:
"""
原地交换位置,得到 pivot 所在索引
:param start:
:param end:
:return:
"""
# 随机选取索引值所在位置
pivot_idx = random.randint(start, end)
pivot = nums[pivot_idx]
idx = start
swap(pivot_idx, start)
pivot_idx = start
for i in range(start, end + 1):
if nums[i] < pivot:
swap(i, idx)
if pivot_idx == idx:
pivot_idx = i
idx += 1
swap(idx, pivot_idx)
pivot_idx = idx
return pivot_idx
pivot_idx = partition(start, end)
if end - pivot_idx == target:
return nums[pivot_idx]
elif end - pivot_idx > target:
# 说明 pivot_idx 所在的数更小
return choose(pivot_idx+1, end, target)
else:
# 比如 2 1 3 4 其中 3 所在的位置大于它的只有 1 个, target 为 2,则我们想要在 2 1 中找 target 为 0
return choose(start, pivot_idx-1, target-1-end+pivot_idx)
return choose(0, len(nums) - 1, k - 1)
扩展题:
347. Top K Frequent Elements github repo
两个有序数组的 topk 问题
两个有序递增数组求第 k 个元素问题
典型例题 4. Median of Two Sorted Arrays https://leetcode.cn/problems/median-of-two-sorted-arrays/
普通实现方式是合并两个有序数组然后求第 k 个元素即可,但还有一种优化方式,
假如我们将 k 一分为二,分别于两个数组找第 k//2 个元素,小的那方以及小的左侧的数字肯定不可能是第 k 个数字,因为其左侧数字的数量肯定低于 k-1
由此排除掉一部分左侧的数字,以此递归
时间复杂度:O(log(M+N))
空间复杂度:O(1)
尾递归(tail recursion): 下一次函数调用不再需要上一个函数的环境了,得到结果立即返回。
普通递归:下次函数调用完成后当前函数还有要执行的内容,因此还需要保存当前的环境以处理返回值。
def findk(nums1: List[int], nums2: List[int], k: int) -> int:
m, n = len(nums1), len(nums2)
def recursion(start1: int, end1: int, start2: int, end2: int, target: int) -> int:
if end1 - start1 + 1 <= 0:
return nums2[start2 + target - 1]
if end2 - start2 + 1 <= 0:
return nums1[start1 + target - 1]
mid = target // 2
idx1 = min(end1, start1 + mid - 1)
idx2 = min(end2, start2 + mid - 1)
if target == 1:
return min(nums1[start1], nums2[start2])
if nums1[idx1] > nums2[idx2]:
return recursion(start1, end1, idx2 + 1, end2, target - (idx2 - start2 + 1))
else:
return recursion(idx1 + 1, end1, start2, end2, target - (idx1 - start1 + 1))
return recursion(0, m - 1, 0, n - 1, k)
汉诺(Hanoi)塔问题
references:
汉诺塔问题
汉诺塔问题以及时间复杂度
引入
该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置n个金盘(如下图)。游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。
思路分析
首先要想达到最终将所有的盘子从A柱子移动到C柱子的目的,肯定经过了这样的三个笼统步骤:
- 1-n-1号盘子从A移动到B上
- n号盘子从A移动到C上
- 将1-n-1号盘子从B移动到C上
显然各个子问题互相不干扰,因此可以采用分治算法,而最佳方案就是递归。
/**
* T(n)=2T(n-1)+O(1)
* 时间复杂度:O(2^n)
*/
const move=(n,x,y)=>{
console.info(`take ${n} move from ${x} to ${y}`);
};
const hanoi=(n,A,B,C)=>{
if(n===1){
move(n,A,C);
}else{
hanoi(n-1,A,C,B);
move(n,A,C);
hanoi(n-1,B,A,C);
}
};
// hanoi(3,'A','B','C');
hanoi(4,'A','B','C');
/**
take 1 move from A to B
take 2 move from A to C
take 1 move from B to C
take 3 move from A to B
take 1 move from C to A
take 2 move from C to B
take 1 move from A to B
take 4 move from A to C
take 1 move from B to C
take 2 move from B to A
take 1 move from C to A
take 3 move from B to C
take 1 move from A to B
take 2 move from A to C
take 1 move from B to C
*/
# 可以使用集中到一个函数的方式
def hanoi(n, a, b, c):
if n == 1:
print(a, '-->', c)
else:
hanoi(n - 1, a, c, b)
hanoi(1, a, b, c)
hanoi(n - 1, b, a, c)
时间复杂度
由 T(n)=2T(n-1)+O(1)可得时间复杂度:O(2^n)-1 取增长最快的项,即为 O(2^n)
例题
leetcode-241-为运算表达式设计优先级
可以看下面是优化后的这个题的题解,是一种分治+暂存结果的方式,但个人认为不隶属于动态规划,因为这是一个先选后解决子问题的模式
/**
* optimize: 暂存每次遍历获得的数值
* @param input
* @returns {[*]|[]}
*/
const diffWaysToCompute=input=>{
let inputArr=[],symbol={'+':true,'-':true,'*':true},st=-1,map=new Map();
for(let i=0;i<input.length;i++){
if (symbol[input[i]]){
inputArr.push(input.slice(st+1,i));
inputArr.push(input[i]);
st=i;
}
}
inputArr.push(input.slice(st+1));
// console.info(inputArr);
const diffCompute=(arr,st,ed)=>{
let res=[];
if (ed-st===1&&!symbol[arr[st]]){
return [Number(arr[st])];
}else{
for(let i=st;i<ed;i++){
if (symbol[arr[i]]){
let left=map.get(`${st}-${i}`)||diffCompute(arr,st,i);
let right=map.get(`${i+1}-${ed}`)||diffCompute(arr,i+1,ed);
for(let j=0;j<left.length;j++){
for(let k=0;k<right.length;k++){
if(arr[i]==='+'){
res.push(left[j]+right[k]);
}else if(arr[i]==='-'){
res.push(left[j]-right[k]);
}else{
res.push(left[j]*right[k]);
}
}
}
}
map.set(`${st}-${ed}`,res);
}
}
console.info('map===>',map);
return res;
};
return diffCompute(inputArr,0,inputArr.length);
};
leetcode-53-最大子序和
这道题被分到分治算法的条目下,当然可以使用分治算法来解决,但是通过观察会发现,或许分割是好分的,下面主要探究如下两个问题:
- 用什么样的思路解决呢?
- 如果解决好了一个子问题,如何进行合并呢?
- 首先我们对测试用例
[-2,1,-3,4,-1,2,1,-5,4]进行分解;- 如果只有一个元素,那么就是它本身
- 如果有两个元素:
[-2,1],那么最大子序和是1毫无疑问,我们如何比较的,肯定是比较:-2,1,-2+1===> 1,由此也有了我们 combine 的主体思路:Math.max(left,right,sum(left,right)) - 如果有三个元素呢?
[-2,1,-3]首先 left 肯定选定为1了 right 即为-3,此时sum(left,right)为 -2,那么按之前的思路,最终结果为 1,正确 - 如果是四个元素呢
[-2,1,-3,4],有关[-2,1]即 left 为 1,有关[-3,4]即 right 为4,最终结果是5,显然错误,如果思路没问题,那么sum(left,right)就有问题,因此将sum(left,right)重新调整计算方式,理应为左侧倒序,右侧正序的相加- 且在此处有一个陷阱点:是否觉得但凡遇到负数即停止遍历呢?,并不是,比如[3,0,2,-2,3],因此应该遍历到最后
- 根据1中的分析可以得到如下代码
/**
* 分治算法,基本思路如下:分成左右两部分,关键在于组合combine部分
* 时间复杂度: O(NlogN)
* 空间复杂度: O(logN) 递归时栈所用的空间
* 注:combine 部分的函数crossSum 乍一看像是有重复计算,实则不然,每个元素都有自己的交叉和。
* @param nums
* @returns {*|number}
*/
const maxSubArray2=nums=>{
const crossSum=(arr,left,right,p)=>{
if(left===right) return arr[left];
let leftSubSum=-Number.MAX_SAFE_INTEGER;
let curSum=0;
for(let i=p;i>left-1;i--){
// 这种判断方式不对,会跳过[3,0,2,-2,3]这种情况,因此此处需要格外注意
// if(arr[i]>=0){
// leftSum+=arr[i];
// }else{
// break;
// }
curSum+=arr[i];
leftSubSum=Math.max(leftSubSum,curSum);
}
let rightSubSum=-Number.MAX_SAFE_INTEGER;
curSum=0;
for(let i=p+1;i<right+1;i++){
curSum+=arr[i];
rightSubSum=Math.max(rightSubSum,curSum);
}
return leftSubSum+rightSubSum;
};
const helper=(arr,left,right)=>{
if(left===right){
return arr[left];
}
// 分解
let p=Math.floor((left+right)/2);
// 解决
let leftSum=helper(arr,left,p);
let rightSum=helper(arr,p+1,right);
// 合并
let crossSum0=crossSum(arr,left,right,p);
console.info('===>',leftSum,rightSum,crossSum0);
return Math.max(leftSum,rightSum,crossSum0);
};
return helper(nums,0,nums.length-1);
};
在了解到这种计算的方式后有一点想法:是否可以直接通过求交叉和的方式将答案求出呢,那么现在试验一下:
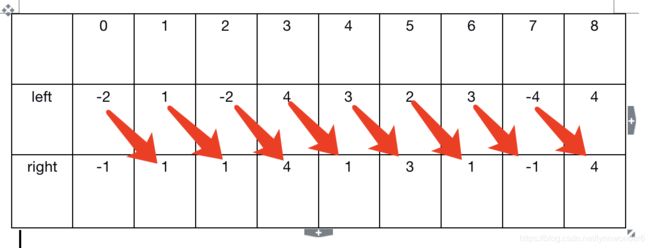
下图中:left每个元素是倒序的leftSubSum。right每个元素是正序的 rightSubSum,可以发现按图示箭头相加即为随意按某个值分割之后的交叉和,得到[-1,2,2,5,6,3,2,0] 其中取最大值即为6.
但是问题来了,求 left 和 right 集合实则时间复杂度为n^2,最终又跳出了暴力解的方式,故不可取。
Kadane algorithm
kadane algorithm实质上是一种动态规划算法,
- 状态转移方程:F(n)=f(n)+F(n-1)>0?F(n-1):0;
- 最优子结构:F(n-1) 显然就是前面 n-1 个序列的子序列最大和,
- 但同时我们需要暂存这些结果避免重复计算
# kadane 伪代码
cur, res = 0, -sys.maxsize-1
for x in nums:
cur = x + max(cur, 0)
# res 实际上是在暂存 cur
res = max(res, cur)
当然这道题用分治算法来做未免有点稍微难绕,这样思考这个问题,我们想要求得的永远都是连续的子序列的和,因此可以求出每一个元素到该元素为止的最大和
/**
* 时间复杂度:O(n)
* 空间复杂度:O(1)
* @param nums
* @returns {*}
*/
const maxSubArray=nums=>{
let res=nums[0];
for(let i=1;i<nums.length;i++){
if(nums[i-1]>0){
nums[i]+=nums[i-1]
}
res=Math.max(res,nums[i]);
}
// console.info(nums);
return res;
};
leetcode-169-多数元素
这道题用来做分治算法的例题很经典,一方面我们可以使用复杂度更低的哈希表来求解。另一方面它也是典型的可以用分治来解决的问题,此题使用分治算法的难点恐怕就在于combine合并环节。
下面总结了两个我的常犯错误:
- 曾试图降级到只有两个元素,显然不对,应该最终都降级为一个元素
- combine的时候未能囊括所有情况(定位不准)
/** 时间复杂度: T(n)=2T(n/2)+2n
* 根据master theorem
* a=2 b=2 f(n)=2n 符合第二种情况,O(n)=nlogn;
* 尽管分治算法没有直接分配额外的数组空间,但因为递归的过程,
* 在栈中使用了一些非常数的额外空间。
* 因为算法每次将数组从每一层的中间断开,所以数组长度变为 1 之前只有 O(lgn)次切断。
* 由于递归树是平衡的,所以从根到每个叶子节点的长度都是 O(logn)。
* 由于递归树是深度优先的,空间复杂度等于最长的一条路径,也就是 O(logn)。
* @param nums
* @returns {*}
*/
const majorityElement2=nums=>{
const count=(arr,num,left,right)=>{
let count=0;
for(let i=left;i<=right;i++){
if(arr[i]===num){
count++;
}
}
return count;
};
const conquer=(arr,left,right)=>{
if(left===right){
return arr[left];
}
let mid=Math.floor((left+right)/2);
let leftRes=conquer(arr,left,mid);
let rightRes=conquer(arr,mid+1,right);
// console.info(leftRes,rightRes);
if(leftRes===rightRes){
return leftRes;
}
return (count(arr,leftRes,left,right)>count(arr,rightRes,left,right)?leftRes:rightRes);
};
return conquer(nums,0,nums.length-1);
};
leetcode-932-漂亮数组
references:
官方题解
/**
* 易错点1: 对于N个数,奇数有多少个,偶数有多少个,奇数floor((N+1)/2) 偶数floor(N/2)
* 易错点2: 映射关系是否可以定为2*x+1呢,可以,但是会不符合题意,超出N的范围
* 总结:该题不易做,很难想到利用奇偶两侧满足的
* @param {number} N
* @return {number[]}
*/
const beautifulArray = N=> {
let map=new Map();
const helper=num=>{
if(num===1){
map.set(1,[1]);
return [1];
}
if(map.has(num)){
return map.get(num);
}
let t=0,res=[];
for(let i of helper(Math.floor((num+1)/2))){
//
res[t++]=2*i-1;
}
for(let i of helper(Math.floor(num/2))){
res[t++]=2*i;
}
map.set(num,res);
return res;
};
return helper(N);
};
Python 版本
class Solution:
def beautifulArray(self, n: int) -> List[int]:
"""
使用分治算法,结合 ka+b 的逻辑得到 2x-1 即为奇数 2x 即为偶数
时间复杂度:O(NlogN) T(N) = 2T(N/2)+N
空间复杂度:O(N) 结果占用空间是 O(N) 而递归调用栈占用空间是 O(logN)
but 题解给出的空间复杂度为:O(NlogN)
:param n:
:return:
"""
if n == 1:
return [1]
odd, even = (n + 1) // 2, n // 2
res = []
for val in self.beautifulArray(odd):
res.append(2 * val - 1)
for val in self.beautifulArray(even):
res.append(2 * val)
return res
summary
对于这种毫无头绪的题目,有时候需要盯着题目中的表达式寻找出路,比如对于A[k] * 2 = A[i] + A[j]可以联想到寻找奇偶数的方向(虽然这很难想
leetcode-190-Reverse Bits
对整型进行位运算的关键:
- 想要获得某一位的数,我们可以将原数 x>>1 右移,并将其 x&1 此时就是转化为二进制后最后一位的数字
- 如果想拼接两个二进制数则用或 | 运算即可
class Solution:
def reverseBits(self, n: int) -> int:
"""
注意是位运算, n 是一个 32 位的无符号整数,所以我们可以依次移动 n 的每一位
获取将二进制位翻转得到的数,由于限制了 n>0 所以时间复杂度为 O(logN)
比如假如 n 是 4,则只需要循环两次即可
时间复杂度:O(logN)
空间复杂度:O(1)
:param n:
:return:
"""
res = 0
for i in range(32):
if n <= 0:
break
res |= (n & 1) << (31 - i)
# n 不停的向右移动一位,这样保证了最后一位总是将要处理的数据位
n >>= 1
return res
def reverseBits_1(self, n: int) -> int:
"""
我们可以采用分治法来解决这个问题,只需要将前一半翻转的答案放在后一半翻转的答案后面即可
位运算的时间复杂度为 O(1)
时间复杂度:已知为 O(log32) 即 O(1)
空间复杂度:已知为 O(log32) 即 O(1)
题解移动奇偶位的算法没看懂
:param
:return:
"""
def recursion(n: int, total: int) -> int:
if total == 1:
return n & 1
mid = total // 2
right = recursion(n, mid)
left = recursion(n >> mid, mid)
return right << mid | left
return recursion(n, 32)
>>> 同类型 leetcode-191-hammingWeight
github repo
leetcode-395-Longest Substring with At Least K Repeating Characters
该题一开始用暴力法解决时会考虑用滑动窗口优化,但由于没法限制窗口大小所以无法优化。但我们可以换个思路思考,将字符串按不符合条件的分成不同部分来进行解决,即分治法。
class Solution:
def longestSubstring_0(self, s: str, k: int) -> int:
"""
寻找一个子数组,其中每个元素出现的个数都大于等于 k
a b a b b c
a 0 1 1 2 2 2 2
b 0 0 1 1 2 3 3
c 0 0 0 0 0 0 1
暴力法是通过一个数组收集每个元素出现的次数,然后遍历所有子数组得到结果
将这个题可以简化成求出现次数 >=k 次的最长子数组
0 1 1 2 3 4 5
:param s:
:param k:
:return:
"""
import copy
length = len(s)
map_list = [{}]
for i in range(length):
tmp = copy.deepcopy(map_list[-1])
if s[i] in map_list[-1]:
tmp[s[i]] += 1
else:
tmp[s[i]] = 1
map_list.append(tmp)
res = 0
# print(map_list)
for i in range(length - k + 1):
for j in range(i + k - 1, length):
flag = True
for item in map_list[j + 1].items():
if item[0] in map_list[i]:
if item[1] - map_list[i][item[0]] < k and item[1] - map_list[i][item[0]] != 0:
flag = False
break
else:
if item[1] < k and item[1] != 0:
flag = False
break
if flag:
res = max(res, j - i + 1)
return res
def longestSubstring_1(self, s: str, k: int) -> int:
"""
假如字符串中含有字符出现次数小于 k,则答案一定是不包含这些字符的子串,此时递归各个子串即可
时间复杂度:T(n) = n + T(x) + T(x) 所以时间复杂度为 O(kN) 因为 T(x) 最多有 26 个记为 Σ,所以为 O(26N) 即 O(N)
空间复杂度:递归深度为 O(Σ),每次需要开辟 O(Σ) 空间,复杂度为 O(Σ^2)
:param s:
:param k:
:return:
"""
length = len(s)
def dfs(l: int, r: int, k: int) -> int:
if l > r:
return 0
map_list = [0] * 26
fault = []
for i in range(l, r + 1):
idx = ord(s[i]) - ord('a')
map_list[idx] += 1
for i in range(26):
if 0 < map_list[i] < k:
fault.append(i)
if len(fault) == 0:
return r - l + 1
res = 0
i = l
start = l
end = l - 1
while i <= r and start <= r and end <= r:
if ord(s[i]) - ord('a') not in fault:
end += 1
else:
if start <= end:
tmp = dfs(start, end, k)
res = max(res, tmp)
start = i + 1
end = i
i += 1
if start <= end:
tmp = dfs(start, end, k)
res = max(res, tmp)
return res
return dfs(0, length - 1, k)
该题也可以使用滑动窗口来解决,参考 详解双指针法