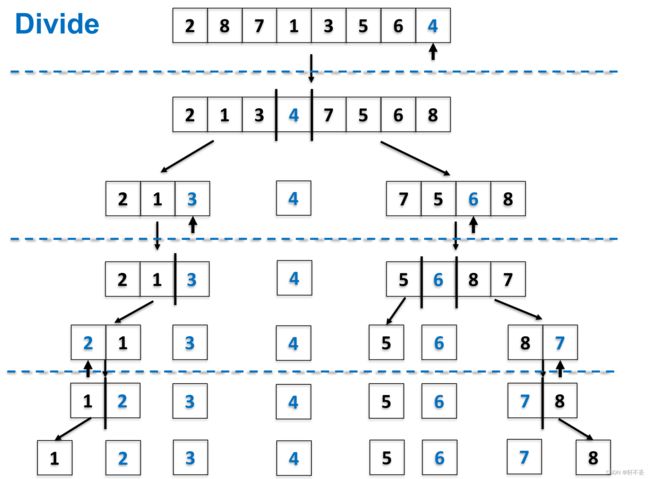
Unit1_3:分治算法之排序问题
文章目录
- 一、归并排序
- 二、快速排序
-
- 思路
- 伪代码
- 流程图
- 时间复杂度
- 改进
- 三、堆排序
-
- 结构
- 插入
- 提取最小值
- 排序
- 抽象
- 四、比较排序总结
-
- 决策树模型
一、归并排序
归并排序子操作的思路和Unit1_2逆序计算一样
下面写一下伪代码
if left < right then
center←L(left + right)/2];
Mergesort(A, left, center);
Mergesort(A, center+1, right);
“Merge” the two sorted arrays;(逆序中的排序思路)
end
else
return A[left]
时间复杂度:
T ( n ) = { 2 T ( n 2 ) + n i f n > 1 1 i f n = 1 T(n)=\left\{ \begin{array}{ll} 2T(\frac{n}{2})+n & if \space n>1 \\ 1 & if \space n=1 \nonumber \end{array} \right. T(n)={2T(2n)+n1if n>1if n=1
在第一节时提及三种计算方式,最后得出复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)
二、快速排序
c语言中的qsort。
思路
每次分成两份,使得 A [ u ] < A [ q ] < A [ v ] A[u]< A[q] < A[v] A[u]<A[q]<A[v] f o r for for a n y any any p ≤ u ≤ q − 1 p≤u≤q- 1 p≤u≤q−1 a n d and and q + 1 + ≤ v ≤ r q+1+≤v≤r q+1+≤v≤r
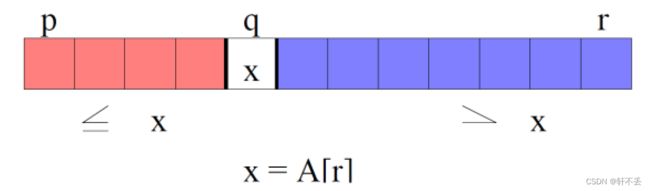
x称为主元。
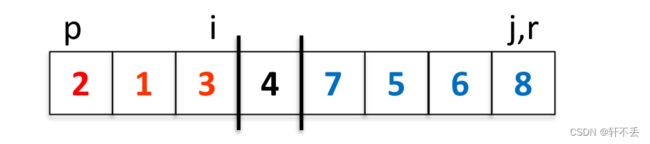
下面看思路图:
起始位置, i = − 1 , j = 0 , p = 0 i=-1,j=0,p=0 i=−1,j=0,p=0
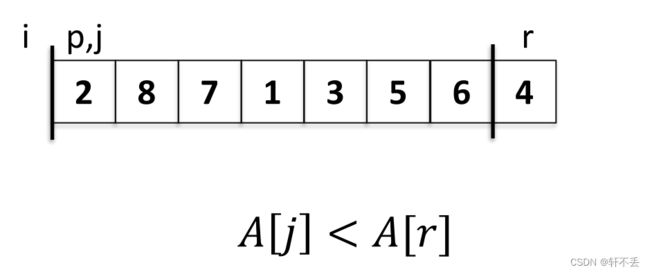
A [ j ] < A [ r ] A[j]
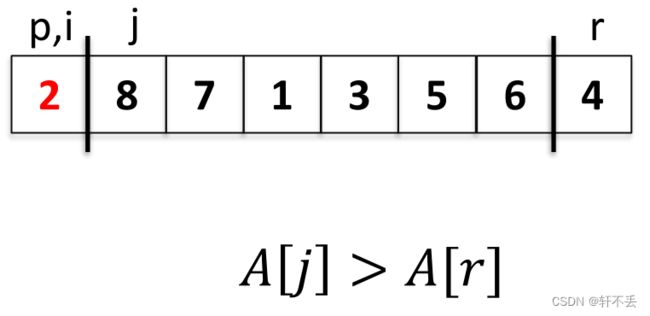
下一个 A [ j ] > A [ r ] A[j]>A[r] A[j]>A[r], j j j++,下一个亦如此
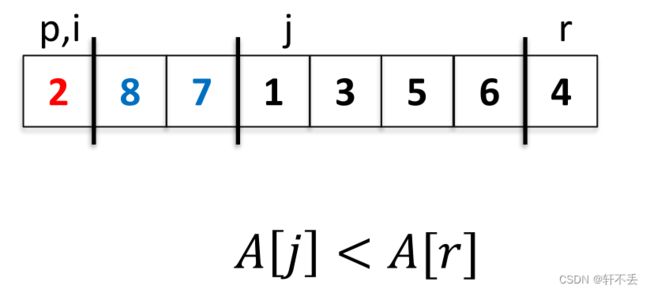
走到 A [ j ] = 1 A[j]=1 A[j]=1,即 A [ j ] < A [ r ] A[j]
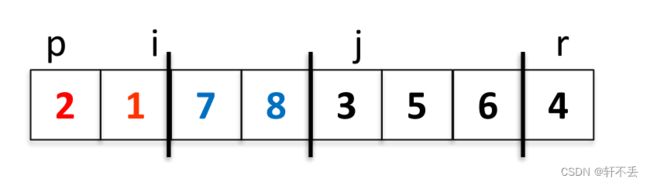
最终j=r时停止
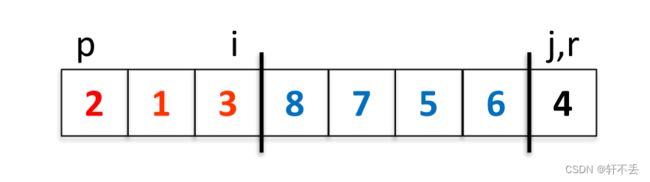
将 A [ i + 1 ] A[i+1] A[i+1]与 A [ r ] A[r] A[r]调换
伪代码
Partition(A,p,r)
x ← A[r]; //A[r] is the pivot element
i ← p-1;
for j←p to r-1 do
if A[j]≤x then
i ← i+1;
exchange A[i] and A[j];
end
end
exchangeA[i+1] and A[r];//Put pivot in position
return i+1; //q ← i+1
这个子操作的时间复杂度为 O ( r − p ) O(r-p) O(r−p)
整个快速排序
Quicksort(A,p,r)
if p流程图
时间复杂度
若总是能将数组分成两半:
T ( n ) = { 2 T ( n 2 ) + n i f n > 1 1 i f n = 1 T(n)=\left\{ \begin{array}{ll} 2T(\frac{n}{2})+n & if \space n>1 \\ 1 & if \space n=1 \nonumber \end{array} \right. T(n)={2T(2n)+n1if n>1if n=1
T ( n ) = O ( n l o g n ) T(n)=O(nlogn) T(n)=O(nlogn)
若最坏情况碰到不平衡分区:
T ( n ) = { T ( n − 1 ) + n i f n > 1 1 i f n = 1 T(n)=\left\{ \begin{array}{ll} T(n-1)+n & if \space n>1 \\ 1 & if \space n=1 \nonumber \end{array} \right. T(n)={T(n−1)+n1if n>1if n=1
T ( n ) = O ( n 2 ) T(n)=O(n^2) T(n)=O(n2)
改进
为了增加算法稳定性,主元采取随机选取的策略:
设 r a n d o m ( p , r ) random(p, r) random(p,r)是一个伪随机数生成器,它返回 p p p和 r r r之间的随机数。
改进算法的时间复杂度计算不难,这里不多赘述,这里用到指标变量。
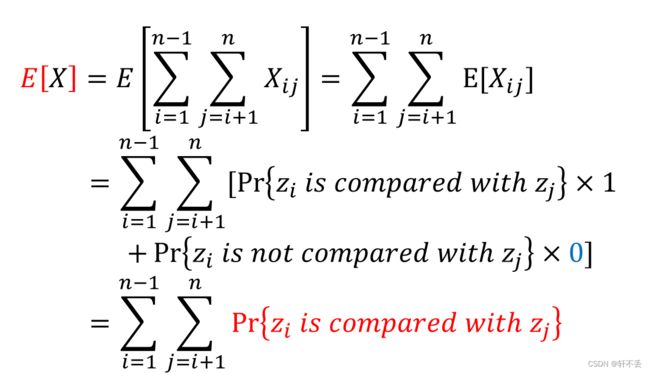

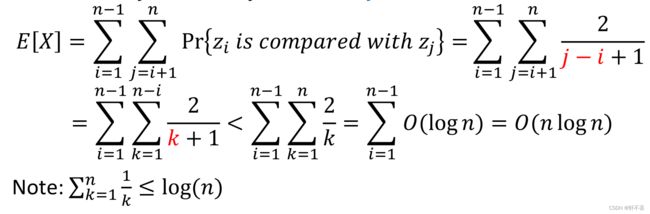
三、堆排序
结构
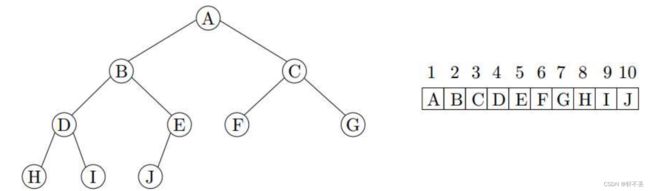
堆本质上就是完全二叉树。除了最低层,所有层都满了。如果最低层未满,则必须将节点打包到左侧。
大顶堆满足父节点值比子节点大,小顶堆满足父节点值比子节点小。
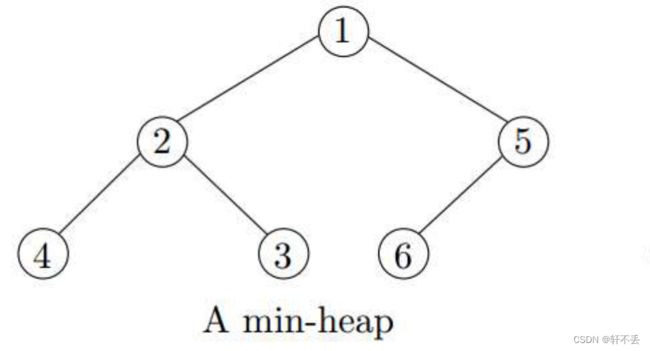
若有 n n n个元素,则树的高度 h = l o g 2 n h=log_2n h=log2n,每次操作一层,则操作的时间复杂度为 O ( l o g n ) O(logn) O(logn)
这种结构可以用数组表示(因为节点都是填满的):
根节点位于数组位置1
对于数组位置i中的任何元素
左子结点位于 2 i 2i 2i位置。
右子结点位于 2 i + 1 2i+1 2i+1位置。
父节点位于位置 i 2 \frac{i}{2} 2i
插入
将新元素添加到最低级别的下一个可用位置,如果违反则恢复最小堆属性
一般策略是向上渗透(或向上冒泡):如果元素的父元素大于元素,则将父元素与子元素交换。
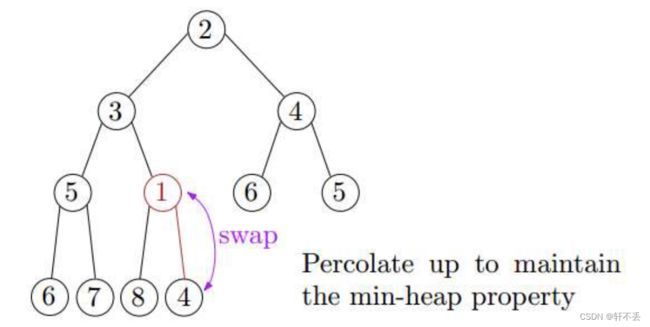
插入的时间复杂度:最坏情况下就是树的高度,因此 T ( n ) = O ( l o g n ) T(n)=O(logn) T(n)=O(logn)
提取最小值
将根节点值拿走后,将最后一个元素复制到根(即覆盖存储在那里的最小元素)
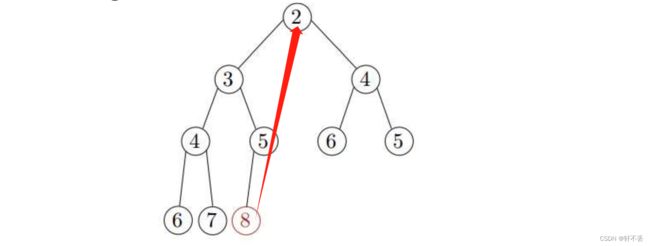
通过向下渗透(或向下冒泡)恢复min-heap属性:如果元素比它的任何一个子元素都大,那么将它与它的子元素中较小的元素交换
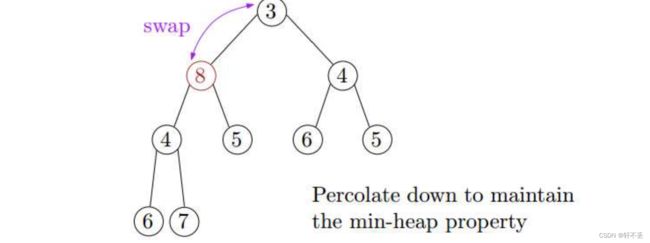
排序
最小元素位于堆的顶部,每次都提取根节点的最小值,然后按上述步骤恢复小顶堆的性质,重复此操作,因为有 n n n个元素,因此时间复杂度 T ( n ) = n O ( l o g n ) = O ( n l o g n ) T(n)=nO(logn)=O(nlogn) T(n)=nO(logn)=O(nlogn)
但排序的前提是要现有一个小顶堆,因此从根节点开始根据小顶堆的性质进行替换
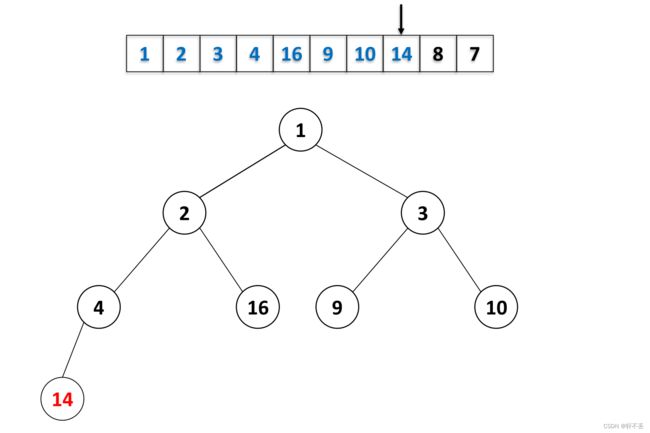
抽象
这和操纵系统的优先级队列一样.事实上确实可以考虑这一算法.优先级队列是一种抽象的数据结构,支持两种操作:插入和提取最小
四、比较排序总结
插入排序,归并排序,堆排序和快速排序都是基于元素比较完成.
事实上,基于元素比较的排序时间复杂度最快就是 O ( n l o g n ) O(nlogn) O(nlogn)
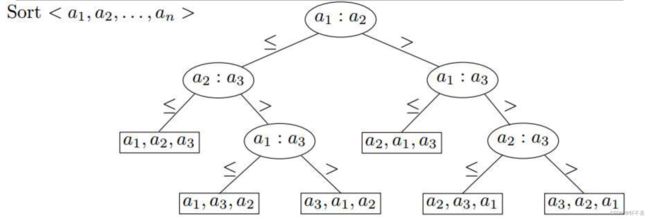
决策树模型
每个叶子对应一个不同的输入顺序
为了使比较排序正确,每个排列必须作为一个叶子出现
决策树可以为任何基于比较的排序算法的执行建模,最坏情况下的运行时间=树的高度