代码随想录算法训练营第十四天|144.二叉树的前序遍历、94.二叉树的中序遍历、145.二叉树的后序遍历
144.二叉树的前序遍历
144.二叉树的前序遍历
每次写递归都要靠直觉? 这次带你学透二叉树的递归遍历!| LeetCode:144.二叉树的前序遍历、94.二叉树的中序遍历、145.二叉树的后续遍历
代码随想录(programmercral.com)
方法一
根据根左右递归遍历即可
代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void preorder(TreeNode* root,vector&result){
if(root!=nullptr){
result.push_back(root->val);
preorder(root->left,result);
preorder(root->right,result);
}
}
vector preorderTraversal(TreeNode* root) {
//递归遍历
vector result;
preorder(root,result);
return result;
}
}; 方法二
使用栈模拟递归函数的过程,根据先序遍历的根左右规则,以及栈先进后出的特性,可以总结出,遍历一个节点的时候,先处理根节点,然后先让右节点入栈,再让左节点入栈 (然后出栈的时候就变成左右了)就算是吧一个节点处理完了,然后每个节点都这么处理就完成遍历了。
代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector preorderTraversal(TreeNode* root) {
//非递归实现前序遍历
stack st;
vector result;
if(root==nullptr) return result;
st.push(root);
while(!st.empty()){
TreeNode* p =st.top();
st.pop();
result.push_back(p->val);
if(p->right) st.push(p->right);
if(p->left) st.push(p->left);
}
return result;
} 94.二叉树的中序遍历
94.二叉树的中序遍历
每次写递归都要靠直觉? 这次带你学透二叉树的递归遍历!| LeetCode:144.二叉树的前序遍历、94.二叉树的中序遍历、145.二叉树的后续遍历
代码随想录(programmercral.com)
方法一
根据左根右递归遍历即可
代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void inorder(TreeNode* root,vector &result){
if(root!=nullptr){
inorder(root->left,result);
result.push_back(root->val);
inorder(root->right,result);
}
}
vector inorderTraversal(TreeNode* root) {
//递归中序遍历
vector result;
inorder(root,result);
return result;
}
}; 方法二
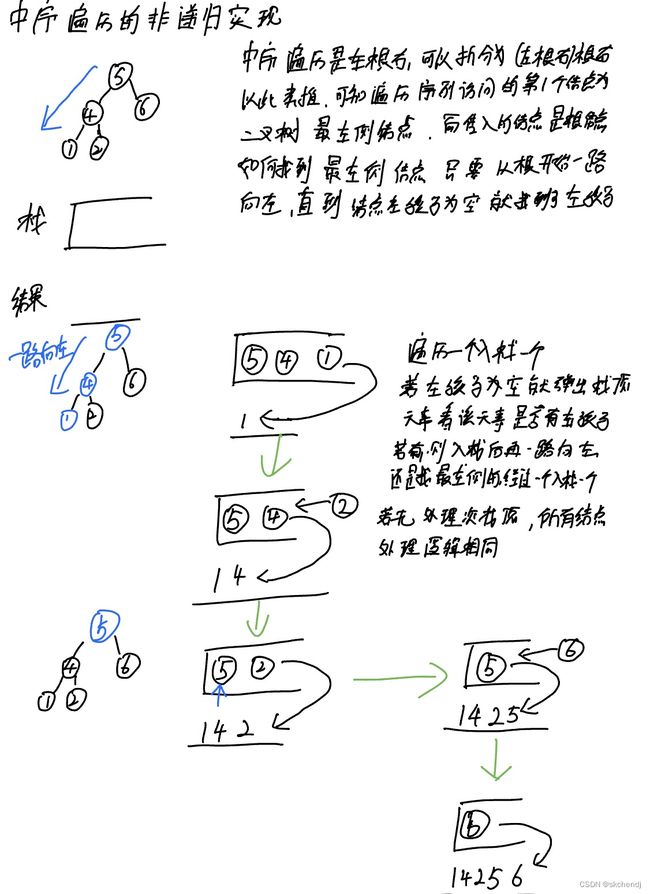
使用栈以及中序遍历的规则实现遍历,中序遍历规则为左根右,然后每个节点都是一颗二叉树,遍历的时候也符合左根右的规则,所以可以带入第一个规则中得到(左根右)根右,然后还可以扩展((左根右)根右)根右,以此类推,即可得到,中序遍历序列中访问的第一个节点是以目前根节点来看的二叉树的最左侧的节点,然后每个节点的处理规则也很容易得到,找到最左侧节点(经过的节点全都加入栈中)后,访问该节点,然后访问该节点,再看看该节点是否有右节点,如果有,就压入栈,其右节点成为新的根节点,同样是找最左侧节点,处理规则同上,若没有右节点,那么就处理次栈顶元素,先访问次栈顶元素,再看有没有右节点,以此类推,直到把所有的节点处理完。即栈为空。
代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector inorderTraversal(TreeNode* root) {
//非递归
stack st;
vector result;
if(root==nullptr) return result;
TreeNode* cur=root;
while(cur!=nullptr||!st.empty()){
if(cur!=nullptr){
st.push(cur);//一路向左
cur=cur->left;
}else{
cur=st.top();
st.pop();
result.push_back(cur->val);
cur=cur->right;//如果不空,就走第一个if 继续找最左侧,如果为空,则走else,用st.top()获取次栈顶元素,依次类推
}
}
return result;
}
}; 145.二叉树的后续遍历
145.二叉树的后序遍历
每次写递归都要靠直觉? 这次带你学透二叉树的递归遍历!| LeetCode:144.二叉树的前序遍历、94.二叉树的中序遍历、145.二叉树的后续遍历
代码随想录(programmercral.com)
方法一
根据左右根递归遍历即可
代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void postorder(TreeNode* root,vector &result){
if(root!=nullptr){
postorder(root->left,result);
postorder(root->right,result);
result.push_back(root->val);
}
}
vector postorderTraversal(TreeNode* root) {
//递归遍历法
vector result;
postorder(root,result);
return result;
}
}; 方法二
使用非递归实现前序遍历的逻辑,区别在于前序遍历的时候是先访问根再让右孩子先入栈,左孩子后入栈,后续遍历则是先访问根再让左孩子先入栈,然后右孩子入栈,这样得到的顺序为根右左,然后对这个结果进行逆置即为左右根,便得到了后序遍历的序列
代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector postorderTraversal(TreeNode* root) {
//非递归实现后序遍历
stack st;
vector result;
if(root==nullptr) return result;
st.push(root);
while(!st.empty()){
TreeNode *p=st.top();
st.pop();
result.push_back(p->val);
if(p->left)st.push(p->left);
if(p->right)st.push(p->right);
}
reverse(result.begin(),result.end());
return result;
}
}; 总结
学到了非递归实现前中后序遍历,特别是后序遍历,从未设想过的道路,可以用前序遍历逆置,并且前序遍历的非递归实现也是一个新知识,需要掌握