运动想象 EEG 信号分析

基于运动想象的公开数据集：Data set IVa (BCI Competition III)¹
数据描述参考前文：https://blog.csdn.net/qq_43811536/article/details/134224005?spm=1001.2014.3001.5501

本文使用公开数据集 Data set IVa 中的部分被试数据，数据已公开可以从网盘获取：
链接：https://pan.quark.cn/s/5425ee5918f4
提取码：hJFz

---

---

1. 实验介绍

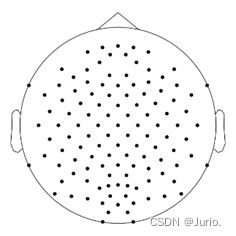
本任务的实验数据来自一名健康受试者，代号al。受试者在视觉提示出现后3.5s内完成以下3个运动想象中的一个：（L）左手，（R）右手，（F）右脚。分类任务中的数据只包括了右手和右脚两类，共280个试次。实验过程中使用脑电帽记录了118个通道的EEG信号，电极位置如图1所示。采集到的EEG信号首先经过带通滤波（0.05-200Hz）,再经过数字化和下采样，得到采样率为100Hz的信号。

图1 电极位置

2. EEG 信号分析

2.1 EEG 的时域特征

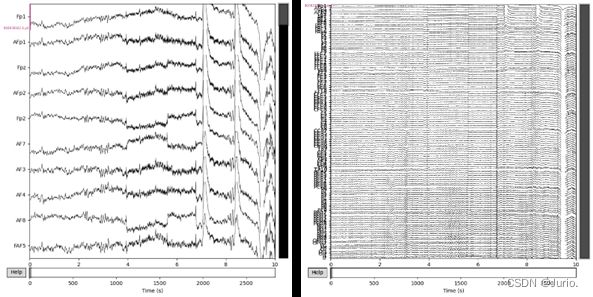
我们首先绘制EEG的时域图，图2(a)和图2(b)分别展示了10个通道和所有通道10s内的信号，可以观察到EEG信号的随机性较强。

(a)                                                                  (b) 图2 EEG时域波形。（a）10个通道的EEG。（b）所有通道的EEG。

2.2 EEG 的频域/时频特征

2.2.1 频域特征

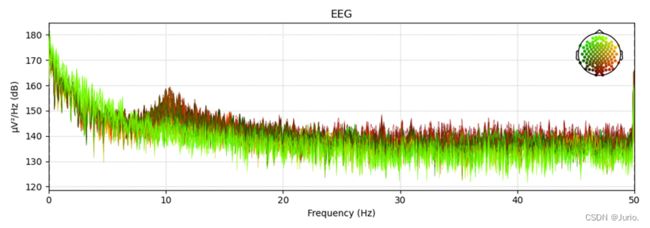
EEG信号是随机信号，通常使用功率谱描述其频域特征。我们截取了100s的EEG信号，使用welch算法估计其功率谱，结果如图3所示。图4则将功率谱按照各电极的位置进行了排列。可以看出：（1）10Hz左右具有明显的峰值，即alpah波；（2）相邻通道的功率谱具有较高的一致性；（3）不同脑区的功率谱具有较大的差异，Alpha波主要出现在枕叶和顶叶区域。

图3 所有通道的功率谱

图4 功率谱按电极位置排列

2.2.2 时频特征

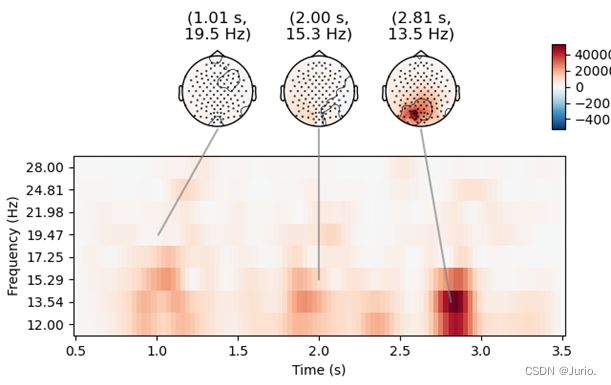
EEG信号具有非平稳的特点，因此需要同时考虑时域和频域。这里，为了更加精细地观察，我们对提示出现后0.5s至3.5s的信号进行分析，并将频率范围限制在12Hz至28Hz。使用Morlet小波变换进行时频域分析，得到的结果如图5所示。可以看出，频率变化在13Hz左右较明显，且枕叶的变化尤为明显。

图5 EEG时频分析结果图

2.3 EEG 的空域（电极位置）特征

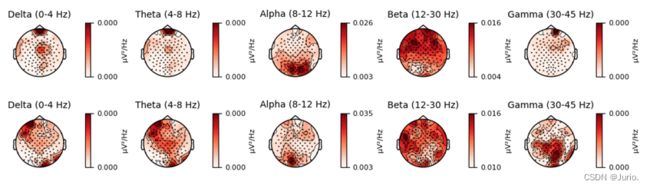
进一步，我们从空域的角度分析EEG，计算两次运动想象期间的功率谱并绘制了5个典型频段的功率谱密度拓扑图，如图6所示。

图6 功率谱密度拓扑图。每一行代表一次事件，每一列代表一个频段

---

3. 分析代码

• 主要使用Python的MNE包进行分析
• MNE Tutorials 官网：https://mne.tools/stable/auto_tutorials/index.html
• 部分变量说明：
  • raw：由 mne.io.RawArray() 函数创建，代表原始EEG数据
  • epochs：由 mne.Epochs() 函数创建，代表一个事件（event）对应的所有数据，在该数据集中一个事件即 “右手”或者“脚”的想象运动

# time domain
raw.crop(tmax=100)
# plot electrode position
plt.figure(figsize=(4,6))
raw.plot_sensors(title='Channel positions')
plt.savefig('Results\sensors.png')
plt.show()

# plot raw eeg data
plt.figure(figsize=(4,6))
raw.plot(n_channels=10, scalings='auto', title='Raw EEG Signals')
plt.show()

plt.figure(figsize=(4,6))
raw.plot(n_channels=118,scalings='auto', title='Raw EEG Signals')
plt.show()

================== plot frequency spectrum
raw.compute_psd().plot()
plt.tight_layout()
plt.savefig('Results\spectrum.png')
plt.show()
raw.compute_psd().plot_topo(color="k", fig_facecolor="w", axis_facecolor="w")
plt.tight_layout()
plt.savefig('Results\spectrum_all.png')
plt.show()



============================ plot time-frequency features
freqs = np.logspace(*np.log10([12, 28]), num=8)
n_cycles = freqs / 2.0  # different number of cycle per frequency
power, itc = mne.time_frequency.tfr_morlet(
    epochs,
    freqs=freqs,
    n_cycles=n_cycles,
    use_fft=True,
    return_itc=True,
    decim=3,
    n_jobs=None,
)
power.plot_joint(
    baseline=(0, 0.5), mode="mean", tmin=0, tmax=3.5,
    timefreqs=[(0.5, 13), (1, 13),(2.8, 13)]
)
plt.show()


epochs[right_id].compute_psd().plot_topomap(ch_type="eeg", agg_fun=np.mean, normalize=True)
plt.savefig(r'Results\right_compute_psd_plot_topomap.png')
plt.show()
epochs[foot_id].compute_psd().plot_topomap(ch_type="eeg", agg_fun=np.mean, normalize=True)
plt.savefig(r'Results\foot_compute_psdplot_topomap.png')
plt.show()

---

1. https://bbci.de/competition/iii/desc_IVa.html ↩︎