【图像分类】【深度学习】【Pytorch版本】AlexNet模型算法详解

【图像分类】【深度学习】【Pytorch版本】AlexNet模型算法详解

---

前言

AlexNet是由多伦多大学的Krizhevsky, Alex等人在《ImageNet Classification with Deep Convolutional Neural Networks【NIPS-2012】》【论文地址】一文中提出的模型，核心思想是使用用一个深度卷积神经网络来进行图片分类，并用dropout这个正则化方法来减少过拟合。
AlexNet的出现标志着神经网络的复苏和深度学习的崛起，成功证明了深度神经网络在大规模图像分类任务中的有效性，为后续的深度学习研究提供了强有力的动力。

---

AlexNet讲解

卷积层的作用

在卷积神经网络里，卷积层的主要功能是通过卷积操作对输入数据进行特征提取。它使用一组可学习的卷积核(也称为滤波器或卷积矩阵)，将卷积核与输入数据进行卷积运算，生成输出特征图。卷积对于提高模型的性能和提取更高层次的抽象特征非常关键。

以下是卷积层在深度学习中的几个重要含义：

1. 特征提取：卷积层可以学习提取输入数据的局部特征。通过卷积核与输入数据进行卷积运算，卷积层能够识别图像中的边缘、纹理、形状等特征。
2. 参数共享：卷积层具有参数共享的特性。在卷积层中，每个卷积核的参数被共享给整个输入数据的不同位置，大大减少网络的参数数量，提高模型的效率，并使模型更具鲁棒性和泛化能力。
3. 空间局部性：卷积层通过局部感受野(receptive field)的方式处理输入数据。每个神经元只连接输入数据中一个小的局部区域，而不是全局连接，能够更好地捕捉输入数据的空间局部性特征。
4. 下采样：卷积层通常结合池化层来进行下采样操作。池化层可以减小特征图的尺寸，并提取更加抽象的特征。
   通过堆叠多个卷积层，可以构建出深度卷积神经网络(Convolutional Neural Network，CNN)，用于解决各种计算机视觉任务(图像分类、目标检测和图像分割)。

卷积过程

在卷积神经网络中，卷积层的实现方式实际上是数学中定义的互相关(cross-correlation)运算，是卷积层中的基本操作，具体的计算过程如图所示：

左边浅紫色的图表示7×7的输入图片(或特征图)矩阵；中间粉红色的图表示3×3卷积核矩阵，后边淡青色的图表示卷积层输出的特征图矩阵。

卷积操作的步骤如下：

1. 将卷积核与输入矩阵的一个局部区域进行逐元素乘积；
2. 对乘积结果进行求和，得到输出矩阵的一个元素；
3. 将卷积核在输入矩阵上移动一个步幅，并重复上述操作，直到覆盖整个输入矩阵；
4. 重复上述过程，每个卷积核生成一个输出矩阵；

卷积过程描述了卷积操作在深度学习中的数学运算，以下是卷积过程中涉及到的重要概念。

概念	描述
卷积核(kernel)	卷积核中数值为对图像中与卷积核同样大小的子块像素点进行卷积计算时所采用的权重
卷积计算(convolution)	图像中像素点具有强烈的空间依赖性，卷积(convolution)就是针对像素点的空间依赖性来对图像进行处理
特征图(feature map)	卷积核的输出结果
填充(Padding)	输入矩阵的边缘周围添加额外的边缘元素(通常是0)，以控制输出矩阵的尺寸
步幅(Stride)	决定了在输入矩阵上卷积核每次移动的距离

特征图的大小计算公式

卷积层输出特征图(矩阵)的大小由以下几个因素决定：

• 输入矩阵的大小:$F_{\mathrm{h}}\times F_{\mathrm{w}}$
• 卷积核的大小:$k_{\mathrm{h}}\times k_{\mathrm{w}}$
• 步幅的大小:$s$
• 填充的大小:$pad$

其基本公式为：
输出特征图的高：$F_{\mathrm{h}}=\frac{F_{h\_prev}-k_{\mathrm{h}}+2\times pad}{s}+1$，输出特征图的宽：$F_{\mathrm{w}}=\frac{F_{w\_prev}-k_{\mathrm{w}}+2\times pad}{s}+1$。
以下是padding为1的输入8×8的输入特征特征矩阵，经过步长为2，大小为3×3的卷积核后生成3×3大小的输出特征矩阵：

同理，池化层输出特征图(矩阵)的大小由以下几个因素决定：

• 输入矩阵的大小:$F_{\mathrm{h}}\times F_{\mathrm{w}}$
• 卷积核的大小:$k_{\mathrm{h}}\times k_{\mathrm{w}}$
• 步幅的大小:$s$

池化层不再对输出特征图进行填充，其基本公式为：
输出特征图的高：$F_{\mathrm{h}}=\frac{F_{h\_prev}-k_{\mathrm{h}}}{s}+1$，输出特征图的宽：$F_{\mathrm{w}}=\frac{F_{w\_prev}-k_{\mathrm{w}}}{s}+1$。
以下是输入4×4的输入特征特征矩阵，经过步长为1，大小为3×3的池化核后生成2×2大小的输出特征矩阵：

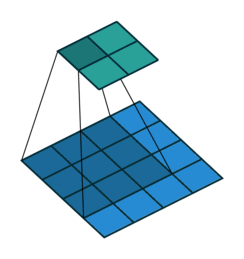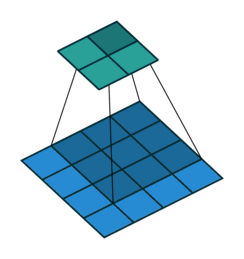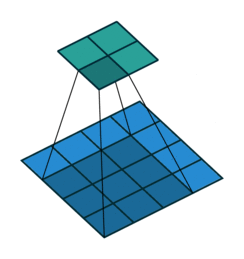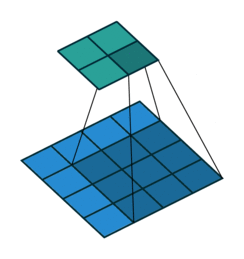
卷积神经网络中池化核的大小通常的为2×2

Dropout的作用

Dropout是一种用于深度神经网络的正则化技术，其核心思想是在训练过程中随机地丢弃(置零)网络中的神经元，即随机地关闭一些神经元(或节点)它们以及与下一层神经元之间的连接，以减少神经元之间的共适应性，从而提高模型的泛化能力。

Dropout的特点：

• 随机关闭神经元：在每个神经元被关闭的概率是相同的，概率是一个给定超参数。
• 前向传播时的关闭：前向传播过程中，失活的神经元的输出值被设为零。
• 反向传播时的开启：反向传播过程中，失活的神经元的权重不会被调整，只有真正激活的神经元参与权重更新。
• 集成学习效果：一种可以集成学习(Ensemble Learning)的方法，因为每次迭代都会随机创建一个不同的子模型，该子模型由丢弃部分神经元后的网络组成，通过平均或投票来集成多个子网络的预测，降低模型的仰角，提高泛化性能。
• 减少共适应性：神经网络中的神经元往往会相互适应，通过彼此的激活模式来共同处理输入数据。这种共适应性可能导致过拟合，即在训练数据上表现良好，但在测试数据上泛化能力较差，特别是在训练数据稀疏或较小的情况下。Dropout通过随机丢弃神经元，迫使网络在不同子集的神经元中学习并适应数据，从而减少神经元之间的共适应性，有助于提高模型的泛化能力。

AlexNet模型结构

下图是博主根据原论文给出的关于VGGnet模型结构绘制的详细示意图：

layer_name	kernel size	kernel num	padding	stride	input_size
Conv1	11	96	2	4	3×224×224
Maxpool1	3	-	0	2	96×55×55
Conv2	5	256	2	1	96×27×27
Maxpool2	3	-	0	2	256×27×27
Conv3	3	384	1	1	256×13×13
Conv4	3	384	1	1	384×13×13
Conv5	3	256	1	1	384×13×13
Maxpool3	3	-	0	2	256×13× 13
FC1	-	2048	-	-	256×1×1
FC2	-	2048	-	-	2048×1×1
FC3	-	1000	-	-	2048×1×1

AlexNet可以分为两部分：第⼀部分 (backbone) 主要由卷积层和池化层(汇聚层)组成，第⼆部分由全连接层 (分类器) 组成。

AlexNet的亮点	说明
ReLU激活函数	解决了SIgmoid在网络较深时的梯度消失问题，训练时比tanh收敛更快，并且有效防止了过拟合现象的出现。
层叠池化操作	池化的步长小于核尺寸，使得输出之间会有重叠和覆盖，可以使相邻像素间产生信息交互和保留必要的联系，提升了特征的丰富性，并且避免平均池化的模糊化效果。
Dropout操作	Dropout操作会将概率小于0.5的每个隐层神经元的输出设为0，选择性地将一些神经节点去掉，减少了复杂的神经元之间的相互影响，达到防止过拟合。

---

AlexNet Pytorch代码

backbone部分

# backbone部分
# 卷积层组:conv2d+ReLU
self.features = nn.Sequential(
            # input[3, 224, 224]  output[96, 55, 55]
            nn.Conv2d(3, 96, kernel_size=11, stride=4, padding=2),
            nn.ReLU(inplace=True),
            # input[96, 55, 55] output[96, 27, 27]
            nn.MaxPool2d(kernel_size=3, stride=2),
            # input[96, 27, 27] output[256, 27, 27]
            nn.Conv2d(96, 256, kernel_size=5, padding=2),
            nn.ReLU(inplace=True),
            # input[256, 27, 27] output[256, 13, 13]
            nn.MaxPool2d(kernel_size=3, stride=2),
            # input[256, 13, 13] output[384, 13, 13]
            nn.Conv2d(256, 384, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            # input[384, 13, 13] output[384, 13, 13]
            nn.Conv2d(384, 384, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            # input[384, 13, 13] output[256, 13, 13]
            nn.Conv2d(384, 256, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            # input[384, 13, 13] output[256, 6, 6]
            nn.MaxPool2d(kernel_size=3, stride=2),
        )

分类器部分

# 分类器部分:Dropout+FC+ReLU
self.classifier = nn.Sequential(
	# 以0.5的概率选择性地将隐藏层神经元的输出设置为零
    nn.Dropout(p=0.5),
    nn.Linear(256 * 6 * 6, 2048),
    nn.ReLU(inplace=True),
    nn.Dropout(p=0.5),
    nn.Linear(2048, 2048),
    nn.ReLU(inplace=True),
    nn.Linear(2048, num_classes),
)

---

完整代码

import torch.nn as nn
import torch
from torchsummary import summary

class AlexNet(nn.Module):
    def __init__(self, num_classes=1000, init_weights=False):
        super(AlexNet, self).__init__()
        # backbone部分
        # 卷积层组:conv2d+ReLU
        self.features = nn.Sequential(
            # input[3, 224, 224]  output[96, 55, 55]
            nn.Conv2d(3, 96, kernel_size=11, stride=4, padding=2),
            nn.ReLU(inplace=True),
            # input[96, 55, 55] output[96, 27, 27]
            nn.MaxPool2d(kernel_size=3, stride=2),
            # input[96, 27, 27] output[256, 27, 27]
            nn.Conv2d(96, 256, kernel_size=5, padding=2),
            nn.ReLU(inplace=True),
            # input[256, 27, 27] output[256, 13, 13]
            nn.MaxPool2d(kernel_size=3, stride=2),
            # input[256, 13, 13] output[384, 13, 13]
            nn.Conv2d(256, 384, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            # input[384, 13, 13] output[384, 13, 13]
            nn.Conv2d(384, 384, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            # input[384, 13, 13] output[256, 13, 13]
            nn.Conv2d(384, 256, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            # input[384, 13, 13] output[256, 6, 6]
            nn.MaxPool2d(kernel_size=3, stride=2),
        )
        # 分类器部分:Dropout+FC+ReLU
        self.classifier = nn.Sequential(
            # 以0.5的概率选择性地将隐藏层神经元的输出设置为零
            nn.Dropout(p=0.5),
            nn.Linear(256 * 6 * 6, 2048),
            nn.ReLU(inplace=True),
            nn.Dropout(p=0.5),
            nn.Linear(2048, 2048),
            nn.ReLU(inplace=True),
            nn.Linear(2048, num_classes),
        )
        # 对模型的权重进行初始化操作
        if init_weights:
            self._initialize_weights()

    def forward(self, x):
        x = self.features(x)
        x = torch.flatten(x, start_dim=1)
        x = self.classifier(x)
        return x

    def _initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                # Conv2d的权重初始化为服从均值为0，标准差为sqrt(2 / fan_in)的正态分布
                nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
                if m.bias is not None:
                    # Conv2d的偏置置0
                    nn.init.constant_(m.bias, 0)
            elif isinstance(m, nn.Linear):
                # FC的权重初始化服从指定均值和标准差的正态分布
                nn.init.normal_(m.weight, 0, 0.01)
                # FC的偏置置0
                nn.init.constant_(m.bias, 0)
if __name__ == '__main__':
    device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
    model = AlexNet().to(device)
    summary(model, input_size=(3, 224, 224))              

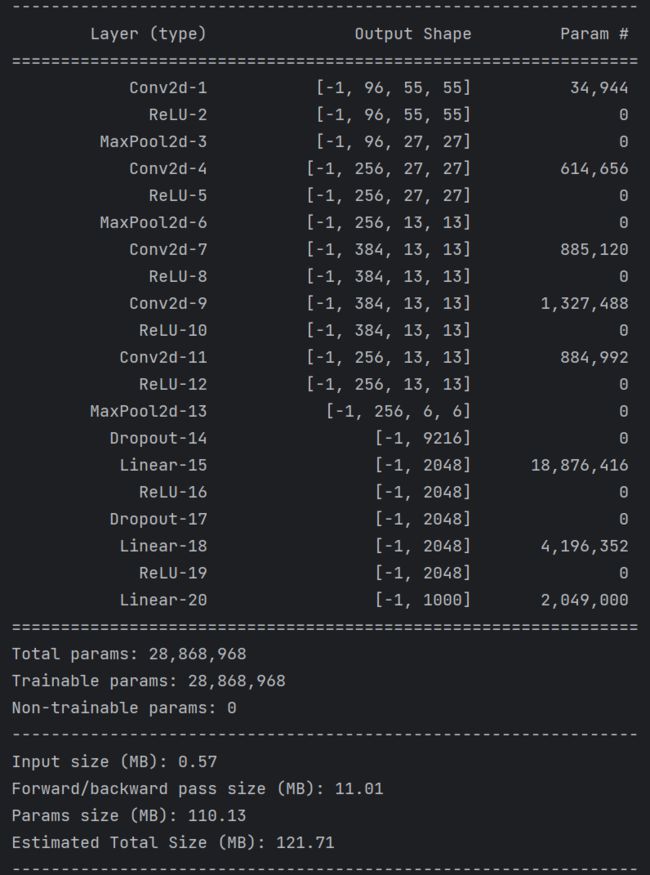
summary可以打印网络结构和参数，方便查看搭建好的网络结构。

---

总结

尽可能简单、详细的介绍了深度可分卷积的原理和卷积过程，讲解了AlexNet模型的结构和pytorch代码。