Reluplex:一种用于验证深度神经网络的高效的SMT求解器
Reluplex:一种用于验证深度神经网络的高效的SMT求解器
-
- 摘要
- 背景介绍
- 背景知识
- 从Simplex到Reluplex
- 高效实现Reluplex
- 案例研究:ACAS Xu系统
- 评估过程
- 总结和未来工作
文献来源:Guy Katz, Clark W. Barrett, David L. Dill, Kyle Julian, and Mykel J. Kochenderfer. Reluplex: An efficient SMT solver for verifying deep neural networks. In Computer Aided Verification, 29th International Conference (CAV), pages 97–117, 2017.
单位:斯坦福大学
摘要
本文提出了一种新颖的、可扩展的、有效的技术来验证深度神经网络的特性(或者提供反例)。该技术基于单纯形方法(Simplex Method),扩展到处理ReLU激活函数。验证程序将神经网络作为一个整体来处理,而不做任何简化的假设。我们在无人机新型机载防撞系统(ACAS Xu)的原型深度神经网络上评估了我们的技术。结果表明,我们的技术可以成功地证明比使用现有方法能验证的最大网络还要大一个数量级的网络的性质。
背景介绍
验证深度神经网络(DNN)性质的困难主要是由激活函数的存在引起的。因为激活函数是非线性的,使得问题是非凸的。本文通过扩展单纯形算法,以持ReLU约束,我们称该算法为Reluplex,意为“带有单纯形的ReLU”。
本文的贡献总结如下:
(1) 提出Reluplex,一个SMT求解器,用于ReLU约束下的线性实数运算理论;
(2) 展示如何把需要验证的的DNN和属性编码为Reluplex的输入;
(3) 讨论对性能和可扩展性至关重要的几个实现细节,例如浮点运算的使用、ReLU变量的边界推导和冲突分析;
(4) 对ACAS Xu系统的实施进行全面评估,证明Reluplex能够扩展到比使用现有技术分析的DNN大一个数量级的DNN。
背景知识

对隐藏层每个节点都应用ReLU激活函数,因此有 v 31 ≡ v 11 v_{31}\equiv v_{11} v31≡v11
可满足性模型理论(SMT,Satisfiability Modulo Theories):
SMT问题是指,针对给定理论T,求解所给公式是否满足T的问题。DPLL(T)结构提供了确定公式的T可满足性的一般方法。
线性实数运算和单纯形方法:
线性运算是加法和数量乘法, 在实数领域像只包含加法和数量乘法二元一次方程就属于线性运算。

对于可行域方程组Ax=b,该方程确定的凸多边形的任意一个顶点对应A的一组基。单纯形算法就是通过反复的基变换(通过向量的进出)来找顶点,从而找到达到最优值的顶点。
从Simplex到Reluplex
在单纯形算法中,问题可以被编码为原子的合取。然而,虽然DNN的权重、偏移值等某些属性可以用单纯形方法编码,但非线性的ReLU激活函数不能。
Reluplex中提出一种思想,首先定义一个解释: R e L U ( x , y ) i f f y = m a x ( 0 , x ) ReLU(x,y)\quad iff\quad y=max(0,x) ReLU(x,y)iffy=max(0,x)
将单个ReLU节点 v v v编码为一对变量 v b v^b vb和 v f v^f vf,然后断言 R e L U ( v b , v f ) ReLU(v^b,v^f) ReLU(vb,vf)。 v b v^b vb用于表示 v v v与前一层节点的连接;而 v f v^f vf用于表示与下一层的连接。

举个简单的例子来说明Reluplex的使用,假设希望检查是否有可能满足 v 11 ∈ [ 0 , 1 ] v_{11}∈[0,1] v11∈[0,1]和 v 31 ∈ [ 0.5 , 1 ] v_{31}∈[0.5,1] v31∈[0.5,1]。通过引入新的基本变量a1、a2、a3,并用等式对网络进行编码,获得初始的Reluplex配置。
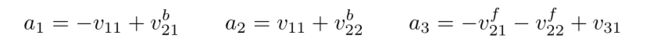
所有变量的初始赋值设置为0。基本变量的下限和上限设置为0,以加强它们所代表的等式。隐藏变量是无界的。
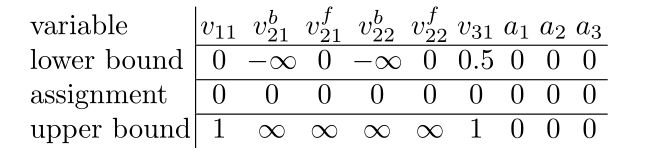
v 31 v_{31} v31的赋值0不在范围0.5~1之间,执行更新,将其设置为0.5。
![]()
此时 v 21 f v_{21}^f v21f赋值为0.5, v 21 b v_{21}^b v21b赋值为0,与ReLU规则不符,因此将 v 21 b v_{21}^b v21b设置为0.5。

此时a2的值为0.5,不符合基本变量值为0的要求。

高效实现Reluplex
这里讨论了三种显著提升Reluplex性能的技术:
- 使用更严格的边界推导
- 冲突分析
- 浮点运算
案例研究:ACAS Xu系统
这是一个机载防撞系统,证明一组输入不会产生错误警报对于证明系统用于安全关键设置至关重要。以前的证明方法包括在150万次模拟遭遇中对系统进行彻底测试,但这不足以证明在连续的DNNs中不存在错误行为。

ACAS Xu为每个离散化的输入组合产生一个网络,网络使用全连接神经网络,带有ReLU激活函数,有6个隐藏层,每个隐藏层共有300个ReLU节点。
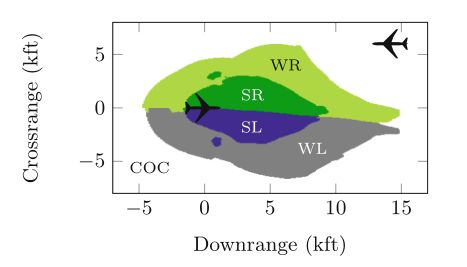
该图显示了一个迎面相遇场景的自顶向下的视图,其中每个像素都被着色,以表示入侵者在该位置时的最佳动作。
评估过程
将Reluplex的实现与最先进的SMT求解器进行了比较:CVC4、Z3、Yices、MathSat以及Gurobi LP求解器。我们在2个ACAS Xu网络(任意选择)上运行了所有的解算器超过4小时,试图求解8个简单的可满足性质。

总结和未来工作
提出了一种新的决策算法,用于解决带有ReLU激活函数的DNN的查询问题。成功地验证了ACAS Xu网络的性质,表明该技术在验证真实世界的DNN方面具有很大的潜力。
将来,我们计划增加这项技术的可扩展性。同时,在不损害性能的情况下提供更好的可靠性保证,例如,使用精确算法重新实现浮点运算方案,或者产生外部可检查的正确性证明。扩展我们的方法来处理带有附加层的DNNs,例如最大池化层。
