【论】Station Importance Evaluation in Dynamic Bike-Sharing Rebalancing Optimization Using an Entropy-B

Station Importance Evaluation in Dynamic Bike-Sharing Rebalancing Optimization Using an Entropy-Based TOPSIS Approach

作者： MINGJIA HE , XINWEI MA , AND YUCHUAN JIN
期刊：IEEE ACCESS
关键字：Bike-sharing, short-term demand prediction, rebalancing demand, station importance, TOPSIS.

摘要

作为一种生态友好的出行方式，共享单车在世界各地盛行。然而，由于用户需求的时空分布不对称，系统是不平衡的。车站优先化策略需要为更重要的车站重新平衡更多共享自行车。本文提出了一种动态共享自行车再平衡中站点重要性的评估方法。首先，应用短期需求预测模型捕获共享单车出行数据的时间和空间特征，并预测车站层面的共享单车需求。基于预测结果，提出了重新平衡量的确定方法，该方法考虑了整个重新平衡期间的自行车共享使用情况。然后，采用三个标准来评估共享单车站的重要性，包括再平衡数量、接近库存阈值和与关键站的距离。提出了一种基于熵的基于理想解相似性的偏好排序技术 Technique for Order of Preference by Similarity to the Ideal Solution（TOPSIS），以衡量不同的标准并评估站点重要性。此外，对南京市自行车共享数据的实验证明了所提方法的有效性。该研究有助于运营商和管理者以高效率动态地重新平衡共享自行车，并提高共享自行车系统的服务质量。

I. INTRODUCTION

共享自行车系统为城市发展带来了新的机遇。它们能够帮助减少机动交通，减少污染物排放，促进社会公平的交通系统[1]，[2]。自行车共享服务还显著提高了旅行者交通资源的灵活性和可达性，为多式联运中的“一英里/最后一英里问题”提供了一个有吸引力的解决方案。全球有2000多个自行车共享系统在运营，300多个系统正在规划或建设中[3]。自行车共享系统可分为停靠式自行车共享系统和无停靠式自行车共用系统[2]、[4]。停靠的自行车共享系统有专用的停靠站，用于自行车出租和归还。相比之下，无坞自行车共享系统允许用户通过手机应用程序在物理或地理围栏指定的停车场租用和停放共享自行车[2]。这两种类型的自行车共享系统都改善了城市交通。然而，由于用户需求的时空分布不对称，这些系统是不平衡的[5]。在一天中的特定时段，一些车站可能会耗尽自行车（不足的车站），而一些车站则没有空间存放归还的自行车（剩余的车站）[6]。鉴于这种情况，需要采取有效措施重新平衡自行车和优化自行车分配。

自行车再平衡的方法可分为基于用户的再平衡和基于操作员的再平衡[7]。基于用户的再平衡方法通过提供货币奖励，鼓励用户在特定站点租赁或归还自行车[7]。然而，站点再平衡的有效性受到用户参与意愿的影响，有时激励措施不会带来预期的经济效益。因此，基于运营商的重新平衡方法被更广泛地用于重新平衡共享自行车[8]。由系统服务人员执行，基于运营商的自行车共享再平衡被建模为多对多取车和送货车辆路线问题many-to-many pickup-and-delivery vehicle routing problem （M-M PVRP），如Berbeglia等人[9]所介绍。在以运营商为基础的自行车共享再平衡过程中，车辆从最初装载自行车的停车场出发，在剩余或不足的车站取下一定数量的自行车，最后返回其原始停车场[6]。

一般来说，自行车再平衡优化可分为静态优化和动态优化[10]。对于静态优化，再平衡操作在夜间进行，假设对自行车的需求可以忽略不计。此优化方法用于在系统中为下一个工作日安排自行车。白天使用动态优化方法，路线需要定期更新，以处理变化的需求。由于运营商重新分配自行车的能力有限，有效的再平衡管理相当困难。特别是在动态再平衡过程中，需求在白天变化，干预资源（如操作时间）有限。因此，需要电站优先化策略来服务于在再平衡过程中更重要的某些电站。重要站点被定义为在网络中比其他站点发挥更重要作用并影响网络结构和功能的站点[11]。评估站点重要性可以帮助运营商决定应优先考虑哪个电站，并实施有效的再平衡[12]。为了改善自行车共享再平衡的决策过程，本研究提出了一种基于多准则决策 multicriteria decision-making（MCDM）方法的站点重要性评估方法。本研究的贡献总结如下：

• 短期需求预测模型用于捕获共享自行车出行数据的时间和空间特征，并预测车站层面的共享自行车需求。预测模型中包括土地利用信息、天气和用户个人信息等外部因素。
• 基于共享单车需求预测结果，提出了确定再平衡量的方法。该方法还考虑了整个再平衡期间的自行车共享使用。
• 采用三个标准来评估自行车共享站的重要性，包括重新平衡数量、接近库存阈值以及与关键站的距离。关键站点定义为正在或将由重新平衡车辆服务的站点。提出了一种基于熵的与理想解相似的偏好排序方法（TOPSIS）来评估站点重要性。

本文的主要内容如下。第2节回顾了共享单车需求预测和共享单车站优先排序的文献。第3节详细介绍了评估站点重要性的方法。第4节进行了实验和讨论结果。最后，第5节总结了结论和未来的研究方向。

II. LITERATURE REVIEW

A. SHORT-TERM BIKE-SHARING DEMAND PREDICTION

短期需求预测对于管理交通基础设施和提高交通系统的可靠性和可达性非常重要。准确的车站级自行车共享需求预测对于动态再平衡过程[2]、[13]、[14]是必要的。通常，数据驱动的自行车共享预测可分为参数方法和非参数方法[15]。当应用统计参数技术时，共享单车需求预测通常被定义为时间序列预测问题。自回归移动平均模型（ARMA）[16]和自回归综合移动平均（ARIMA）模型[17]是众所周知的统计参数方法及其各种变体。例如，使用都柏林的自行车共享数据，Yoon等人[18]提出了一个改进的ARIMA模型，考虑了来自邻近车站的信号和季节趋势，以估计每个车站的可用自行车。其他统计模型已被广泛使用，如贝叶斯网络[19]和马尔可夫链模型[20]-[22]。尽管统计模型更容易解释，但与非参数机器学习模型相比，它们在预测精度、数据可访问性和计算能力方面可能存在局限性[23]。与统计方法不同，机器学习可以自动学习输入和输出之间的关系[24]，而无需对数据结构做出强有力的假设。各种机器学习模型已应用于共享单车预测，如人工神经网络（ANN）[25]、支持向量回归（SVR）[26]和回归树（RT）[27]。Yin等人[28]使用华盛顿特区的自行车共享数据集，应用SVR、随机森林（RF）和梯度增强树（GBT）预测一小时内自行车共享系统的使用情况。他们认为，RF方法在预测精度和训练时间方面表现最好。

最近，深度学习因其能够提取原始数据中的潜在特征和建模非线性关系而吸引了大量研究兴趣。深度学习在许多领域取得了巨大成功，如语言处理和图像识别[29]、[30]。在共享单车研究领域，一些研究人员应用深度学习预测短期出行需求。Lu和Lin[31]将过去一段时间的租金记录输入递归神经网络（RNN），以预测未来一天的自行车租金。Pan等人[32]使用深度长短期记忆（LSTM）序列学习模型，根据历史行程数据、天气数据和时间数据预测单个站点的租金和收益。Xu等人[33]开发了一个LSTM模型，以预测不同预测范围内交通分析区（TAZ）层面的无坞自行车共享需求。此外，Ke等人[34]利用卷积神经网络（CNN），根据历史轨迹数据、天气和城市每个区域的事件，预测每个区域的自行车共享流入和流出。在将整个城市划分为具有预定义网格大小的网格并计算每个网格的共享单车需求后，张等人[35]将CNN应用于大规模时空共享单车预测。为了捕捉空间和时间相关性，研究人员开始将这两种网络结合起来，并提出了卷积LSTM网络（Conv-LSTM）。具体而言，Du等人[36]整合了不规则的CNN和LSTM单元，以捕捉时空交通流的特征，并根据历史客流和外部因素（如天气、交通管制、体育赛事和演唱会）预测一天中不同时间的客流。Ai等人[37]提出了一个Conv LSTM模型，通过考虑时空变量和时间序列变量来预测无坞自行车共享系统的短期分布。Ljubenkov[38]应用卷积神经网络（CNN）识别自行车流的空间结构，RNN-LSTM发现并预测其动态模式。

然而，当CNN用于预测车站层面的共享单车时，它只能通过地理距离反映车站之间的关系[39]。一些研究人员试图将深度学习架构应用于图形数据结构[39]-[42]。以自行车站为节点，自行车共享网络可以用图形表示。一些研究人员在复杂的异质时空图中描述骑车关系，并使用图卷积神经网络（GCN）捕捉非欧几里德结构。Kim等人[39]构建了一个GCN预测模型，通过结合空间特征、时间模式和全球变量（天气和工作日/周末），预测车站层面的每小时共享单车需求。Y oshida等人[40]提出了一种基于关系图卷积网络的方法来预测电站级的需求。Guo等人[41]构建了时空图形神经网络（ST-GNN），以建模和预测全市自行车共享需求。他们使用GCN捕获空间相关性，使用门控递归单元（GRU）捕获时间相关性。肖等人[42]开发了ST-GCN模型，以预测温岭公共自行车共享项目186个站点的接送和返回需求。在他们的研究中，ST-GCN模型在预测精度和计算效率方面优于基于RNN的模型。

先前的研究为自行车共享需求预测提供了有价值的见解。GCN和LSTM的组合使得能够同时捕获时间特征和自行车共享网络结构特征。然而，相关研究还不够.很少有研究充分利用多源异构数据，如天气条件、兴趣点（POI）分布和用户的个人属性[39]。

B. STATION PRIORITIZATION IN BIKE-SHARING REBALANCING

许多研究探索了共享自行车的再平衡问题并提出了解决方案。然而，很少有研究涉及再平衡过程中电站优先级的确定。如表1所示，再平衡数量、接近库存阈值以及与关键站点的距离是常用于评估站点的特征。一些研究根据站点的单一特征做出优先选择。Xu等人[43]提出了一种基于多相似性推理模型的动态调度模型，并采用了增强的遗传算法。在该算法中，改进了混合交叉策略，以优先考虑用户需求较大的站点。为了制定大规模现实世界共享自行车系统的再平衡计划，Mellou和Jaillet[44]优先考虑需要再平衡才能成为领先站点的站点。选择所有引线桩号后，通过将每个桩号指定给其最近的引线来创建桩号的小型组，每个引线都由其引线表示。Federico等人[45]将存活时间定义为站点库存状态超过预定义阈值的最短时间段。他们使用历史使用数据计算存活时间，并在动态短期迁移策略中为存活时间最短的站点分配优先级。如Kadri等人[46]所示，在某些情况下，仅考虑车站的一个特征可能会误导车辆序列的计算。Kadri等人[46]比较了贪婪搜索算法的两种重新平衡优先级策略。第一种策略考虑了不平衡状态和所需的行驶时间，而第二种策略只考虑了所需的行车时间。结果表明，使用兼顾两个方面的策略的算法优于使用第二个策略的算法。基于先前的研究，Brinkmann等人[47]使用安全缓冲区来确定站点是否不平衡。在服务一个不平衡站之后，其最近的不平衡站将首先服务。本杰明[12]使用了一步政策改进方法来决定是否应该重置某个特定站点。数值实验表明，他们的策略优于基于简单优先级规则的策略。它指出，应根据多个标准制定适当的站点优先级政策。

如表1所示，很少有研究能够深入了解电站重要性评估。当采用一个以上的功能时，通常会看到站点重要性是简单决定的，或者是单独考虑的。此外，尚未探索每个特征的权重。Shen等人[16]指出，再平衡距离越远，再平衡成本越高。作为路线优化的基础，通过将站点的不平衡除以再平衡距离来计算两个站点之间的加权路径。Jan等人[48]提出了前瞻性政策，并根据库存为加油站定义了三种不同的目标填充水平。如果站的填充水平违反安全缓冲区，则假定站不平衡。考虑到距离，车辆将在每个决策状态下为最近的不平衡站服务。Zu[49]提出了两种优先级选择方法来生成候选初始解。第一个优先选择惩罚成本降低最显著的车站，第二个优先选择出行成本最低的车站。

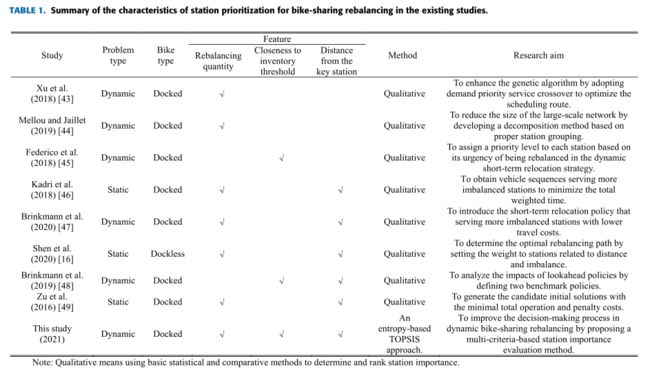
然而，上述研究中没有一项结合了所有三个特征，并对车站重要性进行了全面评估。此外，还没有使用多准则方法来评估共享单车站的重要性。为了填补这些研究空白，本文采用再平衡数量、接近库存阈值和与关键站点的距离作为评价共享站点的三个标准。采用基于熵的TOPSIS方法。TOPSIS 是最流行的 MCDM 方法之一，在该方法中，基于理想解和非理想解的欧几里德距离来评估备选方案[50]。这种方法有助于操作员权衡各种标准并对不同的备选方案进行排序[51]。

III. METHODOLOGY

A. STUDY AREA AND DATA SOURCES

作为江苏省省会，南京长期以来一直被列为华东地区第二大商业中心。为了缓解交通压力，给市民带来极大的便利，南京于2013年推出了对接自行车共享项目。截至2017年，南京约有60000辆停靠共享自行车和450000辆无停靠共享自行车[52]。在图1中，以新街口地铁站为中心，以南京内环路为主要城区。此前对南京停靠共享单车的研究表明，主要城市地区共享单车出行的时间和空间需求存在显著失衡[53]。因此，需要作出相当大的努力来重新分配共享自行车，以保持该地区的高水平服务质量。本研究选取了市中心13个TAZ内的49个车站（新街口地铁站）。图1显示了研究区域的自行车共享站分布。

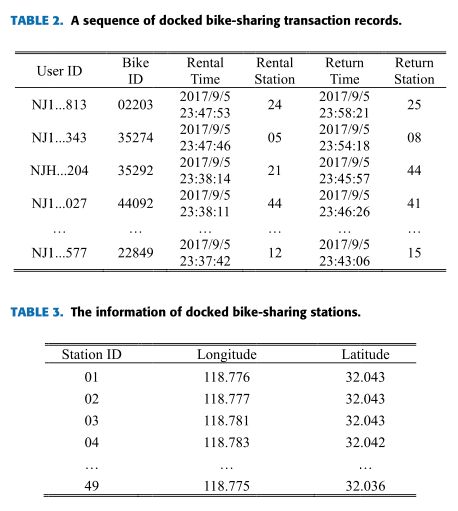
共享单车出行记录、用户个人属性、POI分布和天气条件信息用于共享单车需求预测。共享单车数据集由南京公共自行车公司提供，包括共享单车出行记录、共享单车站信息和用户个人属性。从2017年9月1日至2017年9日30日，共有350701次自行车共享旅行。如表2所示，每个共享单车行程记录用户ID、单车ID、租赁时间、租赁站、返回时间和返回站。预处理数据时，删除了具有以下属性的行程：（1）行程小于100 m或大于5 km[54]；（2） 行程持续时间小于30秒或大于2小时[55]；（3） 信息不完整。表3显示了停靠的自行车共享站的信息，包括站ID、经度和纬度。自行车共享用户的个人属性，包括年龄、性别、居住状态。此外，土地利用数据包含半径为300米的每个自行车共享站的POI和道路密度[56]。POI分为工作POI、住宅POI、交通POI和使用Amap API收集的其他POI[52]。从OpenStreetMap下载道路形状文件，并使用ArcGIS计算道路密度。历史天气信息可从weather Underground获得[57]。

为了评估站点重要性，需要确定三个标准，包括与关键站点的距离、再平衡数量和接近库存阈值。具体而言，关键站和自行车共享站的经度和纬度用于计算与关键站的距离。共享单车需求预测结果、车站容量和车站库存将用于计算再平衡数量。车站容量和车站库存将用于计算接近库存阈值的距离。车站容量和车站库存信息从历史行车记录中提取。

在滚动范围内，预测共享单车需求，然后在每个再平衡阶段评估站点重要性。站点库存和关键站点的更新为再平衡操作提供了准确的信息，如图3所示。

1) BIKE-SHARING DEMAND PREDICTION

长期短期记忆（LSTM）已广泛用于自行车共享需求预测，以捕捉时间序列数据的时间特征[58]、[33]。然而，在这些研究中没有考虑到共享自行车网络的结构特征和车站邻居状态的影响。在先前的研究中，提出了图卷积网络（GCN）来处理具有图结构的数据，例如社交网络数据和气象站网络测量[59]。本文将GCN模型嵌入到LSTM模型中，以预测自行车共享需求。在该GC-LSTM模型中，LSTM应用于捕捉车站级共享单车出行数据的时间特征。GCN用于通过对隐藏层状态执行卷积运算并考虑邻居的隐藏状态对节点隐藏状态的影响来提取共享自行车网络的结构特征。图4显示了GC-LSTM的结构。以下等式解释了图4中符号的含义。



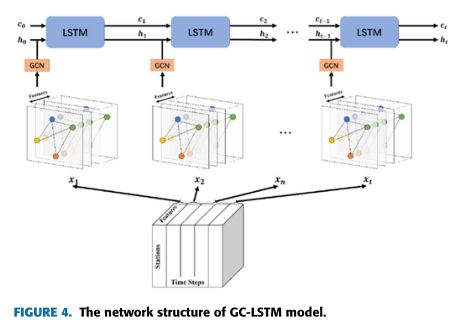
其中 $A_t$表示一个邻接矩阵并作为时间$t$的输入数据。
$h_{t-1}$表示在时间$t-1$的隐藏层。
$W_f,W_u,W_o$,和$b_f,b_u,b_o$分别表示再GCLSTM的3个gates的权重和偏置。
${\sum }_{k=0}^K{\theta }_{hkf}$, ${\sum }_{k=0}^K{\theta }_{h}ku$,${\sum }_{k=0}^K{\theta }_{h}kc$,${\sum }_{k=0}^K{\theta }_{h}ko$,表示图卷积的参数向量。

在本文中，我们构建了一个具有GC-LSTM层的三层神经网络，以预测车站级共享自行车的租赁和归还需求。该模型可以基于LSTM和GCN的组合结构自动学习站点间的时间和空间信息。为了评估拟议模型的性能，使用了平均绝对误差（MAE）和均方根误差（RMSE），正如Lin等人[61]所做的那样：

其中，$x_i$表示观测值，${\hat{x}}_i$表示预测值，$n$表示测试样本的数目。

2) STATION IMPORTANCE EVALUATION

a: CRITERIA DETERMINATION

本文基于再平衡数量、接近库存阈值和与关键站点的距离等多个标准来评估站点重要性。本节介绍了这些标准的定义和计算方法。

Rebalancing quantity: 在以前的研究中，再平衡量完全由预测结果决定，而不考虑库存[43]，或者在再平衡时，它应该为站提供固定的填充水平（在O’Mahony的研究中为50%[62]）。然而，在动态再平衡中，一些已经服务的车站在高峰时段可能仍然有自行车过剩或自行车不足。这是因为共享自行车的需求变化很快，而且会不时变化，尤其是在高峰时期。为了解决这一问题并提高再平衡效率，本研究考虑了再平衡阶段之间的需求变化。其目的是在整个再平衡过程中减少未满足的需求。基于需求预测、站点库存和站点容量，介绍了共享单车再平衡量的计算方法。

在滚动范围rolling-horizon再平衡操作的每个阶段计算再平衡量。设$t_0$表示再平衡操作的开始时间，$\tau$表示再平衡运行的持续时间。地平线将操作分为$n$个阶段，每个阶段的持续时间为$l$。不同阶段描述为时间间隔:$[t_0,t_0+l],[t_0+l,t_0+2l],\cdots ,[t_0+(n-1)l,t_0+nl]$.让$ini{t}_{k，i}$表示在阶段$e_k$站点$i$可用的初始自行车数量。站$i$在阶段$e_k$可用的自行车数量可以描述为：

$v_{i，k}$表示阶段$e_k$的租金率和回报率rental rate and return rate 之间的差异。方程式如下:

其中$N_{i,k}^{pred,rent}$和$N_{i,k}^{pred,return}$分别表示在区间$[t_0+kl,t_0+\tau ]$时站点$i$的预测租赁数量和返回数量predicted rental quantities and return quantities。

考虑到用户租用和归还自行车的不确定性，应为每个站点设置再平衡阈值的上限和下限。设$C_i$表示最大站点容量。根据先前的研究和运行经验[63]，[64]，一般情况下，$i$站再平衡阈值的上限和下限分别设置为$0.2C_i$和$0.8C_i$。$t{w}_{i,k}$表示在滚动期间rolling period的站点的警告时间warning time.这个参数表示在$t{w}_{i,k}$时刻，在站点$i$的可用自行车的数目达到再平衡阈值的上限/下限。$t{w}_{i,k}$可以被计算为：

对于需要在滚动范围内重置的站点，站点的自行车重新平衡数量如图5所示。红线表示每个时段内站点可用的自行车数量，无需重新平衡操作。绿线表示每段时间内重新平衡运行的车站可用自行车数量。具体而言，本研究旨在在整个再平衡阶段保持电站库存不超过再平衡阈值的上限或下限。

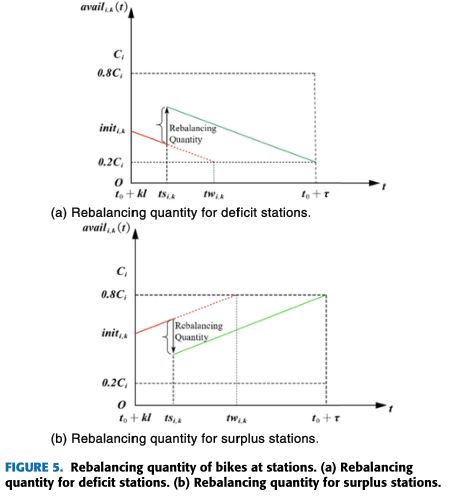
确保赤字站点deficit station的库存在滚动期结束前不会低于再平衡阈值的下限（$0.2C_i$），并确保盈余站点suplus station的库存不会超过再平衡阈值上限（$0.8C_i$）。赤字站（$\gamma =0.2$）和盈余站（$\gamma =0.8$）的再平衡量可通过以下公式计算：

Closeness to inventory threshold: 更高水平的接近库存阈值意味着更容易达到这些站点的库存阈值，更容易出现自行车或码头的缺乏。因此，将更加重视接近库存阈值的站点。接近库存阈值可以在等式（13）中计算。

其中$avai{l}_{i,k,t}$表示在阶段$e_k$和站点$i$的可用自行车数目。

==Distance from the key station: == 到关键站的距离表示未服务站和关键站之间的距离。值得注意的是，在重新平衡操作过程中更新了关键站。在这项研究中，假设停车场是第一个再平衡阶段的城市中心。哈弗辛公式Haversine formulation用于计算从未服务站点到关键站点的距离[65]。

其中$la{t}_k,lo{n}_k$表示关键站点key station的纬度和经度。$la{t}_i,lo{n}_i$表示未服务站点$i$的纬度和经度。$R$表示地球半径。

b: THE ENTROPY-BASED TOPSIS APPROACH

由Hwang和Yoon[66]开发的 TOPSIS 方法是一种 MCDM 技术，基于这样的概念，即所选择的备选方案应同时具有与理想解的最短距离和与非理想解的最大距离。在本研究中，基于熵的TOPSIS方法被应用于基于三个准则的站点重要性评估。评估站点重要性的过程可在以下步骤中描述。

• 步骤1：构造归一化决策矩阵：
  
  其中$x_{ij}$是第$i$个站点相对于第$j$个标准的输出结果；
  $m$是再平衡站点的数目;
  $n$是标准的数目($n=3$).

• 第二步：计算加权归一化决策矩阵。熵方法用于确定权重$w_j$。
  

• 步骤3：确定理想方案A+和非理想方案A−:
  
  其中$J$与福利标准benefit criteria相关，$J=\{j=1,2,\cdots ,n|j\}$;$J^{\prime }$与成本标准cost criteria 相关，$J^{\prime }=\{1,2,\cdots ,n|j\}$.

• 步骤4：确定每个备选方案的理想解和非理想解的欧几里德距离：
  

• 步骤5：计算TOPSIS得分
  
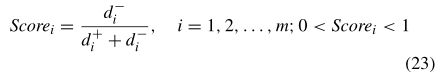
  其中$Scor{e}_i$是站点$i$与一个非理想方案nonideal solution的相对距离，这意味着站点$i$的重要性。TOPSIS得分较高的站点应获得服务优先级[11]。

IV. RESULTS

本文中，再平衡操作持续时间为60分钟，从上午8点开始，到上午9点结束。由于实时需求的差异，应适当调整再平衡操作，以便为用户提供更好的服务。因此，需要经常更新电站重要性[67]、[68]。正如Marte和Kristine[68]、Yu[69]和Feng[70]所建议的，本文将地平线分为四个阶段，每个阶段的持续时间为15分钟。预测范围的持续时间设置为30分钟。如图2所示，下一个预测和运行周期在最后一个运行周期结束时激活。以再平衡运行的第一阶段为例，本文的实验说明了如何基于GC-LSTM模型预测共享单车需求，并基于基于熵的TOPSIS方法评估站点重要性。随着关键站点和站点库存的更新，下一阶段应用预测和评估的过程将与第一阶段相同。

A. BIKE-SHARING DEMAND PREDICTION

实验在工作日使用共享单车出行进行，将前12天生成的数据作为训练数据集，随后4天的数据作为验证数据集，最后5天的数据用作测试数据集。在每个模型中，分别生成两个输出层来预测租金需求和回报需求。为了处理尺寸问题，应用最小和最大归一化。使用网格搜索搜索超参数、学习率、批次大小和隐藏单元的数量。具体来说，学习率从0.001开始，以0.001的步长结束于0.01；批次大小和隐藏单元的数量都从32开始，以128结束，步长为32。为了防止过拟合，为提前停止过程设置了标准。如果验证的MAE在超过10个训练周期内没有减少超过0.00001，则模型将停止训练。预测模型由Python编码。所有实验都在Windows 10计算机上进行，CPU（Intel（R）Core（TM）i7-8700 [email protected]）、16 GB随机存取存储器（RAM）和一台NVIDIA RTX 2060 GPU（6 GB内存）

为了验证GC-LSTM模型在动态再平衡中的自行车共享需求预测性能，在相同的参数设置和编码环境下，将所提出的GC-LSTM模型与实际自行车共享数据集上的基线模型进行了比较，介绍如下。

• 历史平均（HA）：使用同一预测期的历史平均需求进行预测。
• 支持向量回归（SVR）：它使用基于核的径向基函数将特征向量转换为线性高维空间。该方法可以有效地代替高维空间中的复杂计算。
• 极端梯度提升（XGBoost）：它是梯度提升决策树的实现。所有特征都被放置在一维向量中并用于预测。它通过二阶导数优化损失函数，并应用正则化模型来防止过度拟合。
• 人工神经网络（ANN）：它起源于生物神经网络（BNN）。该方法能够从一组输入-输出参数空间中学习，并且能够用不需要系统详细信息的高维数据近似函数。
• 图卷积网络（GCN）：它是一种基于图结构数据的多层神经网络。卷积层使网络能够通过融合节点的特征和节点之间的关系来构建节点嵌入。
• 长短期记忆（LSTM）：它是一种长短期记忆神经网络。作为RNN的改进版本，LSTM可以处理消失梯度和复杂的时间相关性。

表4显示了基于10次训练结果的不同预测区间中每个模型的RMSE和MAE。对于租赁需求和退货需求，当预测间隔变短时，RMSE和MAE变小。具有15分钟间隔的GC-LSTM模型在四个预测间隔中具有最佳性能。此外，模型比较结果表明，基于GC-LSTM的自行车共享需求预测模型优于同类模型。与LSTM结构相比，RMSE和MAE分别下降20.5%和27.91%，租金需求预测的间隔为15分钟，回报需求预测为24.69%和31.82%。值得注意的是，GC-LSTM模型的性能比LSTM模型提高得更快。这可能是因为，与LSTM模型相比，GCLSTM模型在共享自行车图结构中捕捉到更多的波动特征。在Zhang等人的研究中可以发现类似的结果[71]，随着时间间隔的减小，基于GCN的模型的性能比基于LSTM的模型提高得更明显。

B. STATION IMPORTANCE EVALUATION

初始库存和站点容量可基于历史自行车共享数据获得。GC-LSTM模型预测了未来30分钟的共享单车需求。再平衡数量由共享单车需求、初始库存和车站容量决定。接近库存阈值由初始库存和站点容量决定。此外，使用哈弗辛公式计算了与关键站key station的距离。表5显示了站点重要性评估的三个标准的结果。

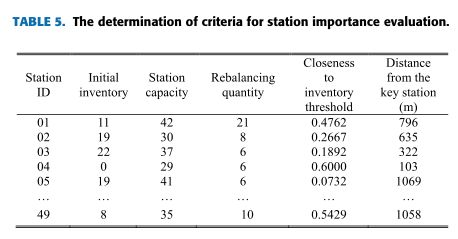
在获得站点级三个标准的值后，采用基于熵的TOPSIS方法评估共享自行车站点的重要性。熵被用来衡量影响站点重要性的再平衡量、接近库存阈值和与关键站点key station的距离。

结合再平衡量、接近库存阈值和与关键站的距离的决策矩阵可从表5中获得。计算结果如表6所示。TOPSIS 方法的第一步是使用等式（15）计算归一化决策矩阵。然后通过等式（16-18）计算加权决策矩阵。值得注意的是，加权决策矩阵是通过将归一化决策矩阵乘以三个准则的权重而获得的。理想和非理想解由方程（19）和方程（20）计算。然后，通过等式（21）和等式（22）计算到理想解和非理想解的距离。最后，根据与理想解的相对接近度，通过等式（23）计算所有备选方案（自行车共享站）的等级。表7显示了重要性排名前10位的站点信息，包括站点ID、与理想和非理想解的距离、TOPSIS得分和重要性排名。


如表6所示，使用熵方法计算三个标准的权重。与关键站的距离权重为52.22%。这种考虑在站点重要性评估中起着核心作用。重新平衡数量在自行车共享中起着重要作用，占24.15%，而最低重要性与接近库存阈值相关（23.63%）。

表7中 TOPSIS 方法的结果表明，19号站排名第一，因为它获得了最高的 TOPSIS 得分（0.8721）。该站距离理想解的距离也最短（0.0167）。结果还显示，4号站的TOPSIS得分为0.4163，在所有站中排名第二。图6显示了站点重要性评估的空间分布。在车辆路线规划中，应优先考虑排名较高的共享单车站。如图6所示，大多数具有高度重要性的站点聚集在关键站点周围。其中一个主要原因是，根据表6中每个标准的加权方面的结果，距离关键站的距离是影响站点重要性的最重要因素。在图6中，一些站点获得了相对较高的排名，尽管它们距离南部的关键站有点远。这些车站也应实施再平衡操作，以更好地提高服务质量。

V. CONCLUSION

本研究提出了一种更有效的动态自行车共享再平衡的站点重要性评估方法。再平衡数量、接近库存阈值和与关键站的距离是评价共享单车站的三个标准。短期共享单车需求预测采用GC-LSTM模型，考虑土地利用信息、天气和用户个人信息等外生因素，以更高精度确定再平衡量。LSTM和GCN的组合使得能够捕获时间特征和自行车共享网络结构特征。实验表明，使用南京停靠自行车共享数据集，GC-LSTM 模型优于基线模型。然后，再平衡量的确定是通过考虑整个再平衡期间的自行车共享使用来确定的。熵方法用于衡量不同标准的影响。然后，采用 TOPSIS 方法对站点重要性进行评估，并对站点进行排序。

数值算例说明了所提出的方法。获取了南京市停靠共享单车的智能卡数据，提取了市中心13个TAZ内的49个站点。建立了具有不同预测区间的GC-LSTM模型，并计算了RMSE和MAE以说明模型的性能。结果表明，间隔15分钟的GC-LSTM模型具有最佳性能。在计算了再平衡量、与库存阈值的接近度以及与关键站点的距离之后，采用基于熵的TOPSIS方法对共享站点的重要性进行了评估。熵方法结果表明，距离关键站点的距离对站点重要性影响最大，权重为52.22%。据指出，靠近关键站的许多站获得了高度重视。同时，由于其他标准水平较高，也有一些站点分布在远离重点站点的地方，排名较高。GC-LSTM模型的平均计算时间为5.9秒。基于熵的 TOPSIS 方法为1.4秒。在实际的自行车共享再平衡操作中，运行时间是可以接受的。

本研究的结果有助于运营商更好地决定在再平衡过程中应优先考虑哪些电站。它也可以应用于基于用户的操作。Ji等人[72]认为，更高的货币激励将鼓励用户参与自行车共享再平衡，并显著缓解自行车共享失衡问题。站点重要性评估有助于确定用户应首先重新平衡哪些站点。通过向更重要的电台分配更高的货币奖励，可以鼓励用户参与这些电台的再平衡。此外，该框架是为停靠自行车共享而设计的，因此由于缺乏固定站，无法直接应用于无停靠自行车共享。然而，与停靠自行车共享类似，无停靠自行车共享再平衡的决策过程仍然需要考虑多个标准，如再平衡车辆的行驶距离、再平衡数量。

对于不同地理位置的不同自行车共享数据集，理论上，GC-LSTM能够捕获自行车共享数据的时间和空间特征。站点重要性评估的结果可能与本案例研究不同，标准的权重可能不同。这是因为基于熵的TOPSIS可以挖掘数据集特征，考虑到自行车共享系统中不同的关键站点、站点分布和出行模式。这项研究有几个局限性，需要在未来的研究中加以解决。首先，本研究仅以南京停靠共享单车为个案研究。如果其他共享自行车数据集可用，可以使用本研究中的方法进行更多实验，以进一步验证和验证。其次，这个框架不能直接在无码头自行车共享上实现。没有固定站可供无坞自行车共享。因此，为分散式无坞共享自行车生成虚拟站点并计算装载和卸载时间是未来研究的关键问题。第三，本研究仅描述了滚动地平线中再平衡的第一阶段，以说明如何使用GC-LSTM模型预测共享单车需求，并基于多标准评估站点重要性。为了完成整个再平衡过程，应解决取车和送货车辆路线问题，以更新关键站和共享单车站库存。然后，可以调查以下再平衡阶段，并进行比较，以研究车站优先顺序如何改善车辆路线规划。第四，共享单车需求预测对于动态再平衡过程是必要的。在本文中，GC-LSTM模型预测了车站层面的自行车共享需求，以提出车站重要性评估策略。尽管GC-LSTM模型在南京共享单车数据集上的性能优于基线模型，但可以进一步探索最新预测模型，如基于时间卷积网络（TCN）的方法或基于双阶段注意力的递归神经网络（DARNN）方法，以提高共享单车需求预测的准确性。最后，可以使用其他MCDM方法，并将获得的结果与当前的研究结果进行比较。未来的研究可以继续采用模糊MCDM方法来处理共享自行车日常使用中的不确定性。这将有助于运营商和管理者以高效率动态地重新平衡共享自行车，并提高共享自行车系统的服务质量。

---