数据结构与算法-链表
数据结构与算法-链表
- 1 链表结构
-
- 1.1 单向链表结构
- 1.2 双向链表结构
- 2 3种单向链表的反转方法
- 3 单向链表区间反转
- 4 单向链表返回倒数k个节点问题
- 5 k个一组反转问题
- 6 链表回文问题
- 7 单向链表区间划分问题
- 8 判断链表是否有环
- 9 复制含有随机指针的链表
- 10 链表相交的一系列问题
-
- 1 第一个入环节点
- 2 两个无环链表的公共节点
- 3 两个有环链表的公共节点
- 11 合并两个已排好序的链表
在正式开始链表之前,先简单了解一下hash表 (与标题无关)
哈希表的简单介绍
1)哈希表在使用层面上可以理解为一种集合结构
2)如果只有key,没有伴随数据value,可以使用HashSet结构(C++中叫UnOrderedSet)
3)如果既有key,又有伴随数据value,可以使用HashMap结构(C++中叫UnOrderedMap)
4)有无伴随数据,是HashMap和HashSet唯一的区别,底层的实际结构是一回事
5)使用哈希表增(put)、删(remove)、改(put)和查(get)的操作,可以认为时间复杂度为O(1),但是常数时间比较大
6)放入哈希表的东西,如果是基础类型,内部按值传递,内存占用就是这个东西的大小
7)放入哈希表的东西,如果不是基础类型,内部按引用传递,内存占用是这个东西内存地址的大小
有序表的简单介绍
1) 有序表在使用层面上可以理解为一种集合结构
2) 如果只有key,没有伴随数据value,可以使用TreeSet结构(C++中叫OrderedSet)
3) 如果既有key,又有伴随数据value,可以使用TreeMap结构(C++中叫OrderedMap)
4) 有无伴随数据,是TreeSet和TreeMap唯一的区别,底层的实际结构是一回事
5) 有序表和哈希表的区别是,有序表把key按照顺序组织起来,而哈希表完全不组织
6) 红黑树、AVL树、size-balance-tree和跳表等都属于有序表结构,只是底层具体实现不同
7) 放入哈希表的东西,如果是基础类型,内部按值传递,内存占用就是这个东西的大小放入哈希表的东西,如果不是基础类型,必须提供比较器,内部按引用传递,内存占用是这个东西内存地址的大小
8) 不管是什么底层具体实现,只要是有序表,都有以下固定的基本功能和固定的时间复
杂度
有序表的固定操作
1)void put(K key, V value):将一个(key,value)记录加入到表中,或者将key的记录更新成value。
2)V get(K key):根据给定的key,查询value并返回。
3)void remove(K key):移除key的记录。
4)boolean containsKey(K key):询问是否有关于key的记录。
5)K firstKey():返回所有键值的排序结果中,最左(最小)的那个。
6)K lastKey():返回所有键值的排序结果中,最右(最大)的那个。
7)K floorKey(K key):如果表中存入过key,返回key;否则返回所有键值的排序结果中,key的前一个。
8)K ceilingKey(K key):如果表中存入过key,返回key;否则返回所有键值的排序结果中,key的后一个。
以上所有操作时间复杂度都是 O ( l o g 2 n ) O(log_2^n) O(log2n), n n n 为有序表含有的记录数
1 链表结构
1.1 单向链表结构
public static class Node<V> {
V e;
Node next;
}
由以上结构的节点依次连接起来所形成的链叫单链表结构
1.2 双向链表结构
public static class Node<V> {
V e;
Node next;
Node last;
}
2 3种单向链表的反转方法
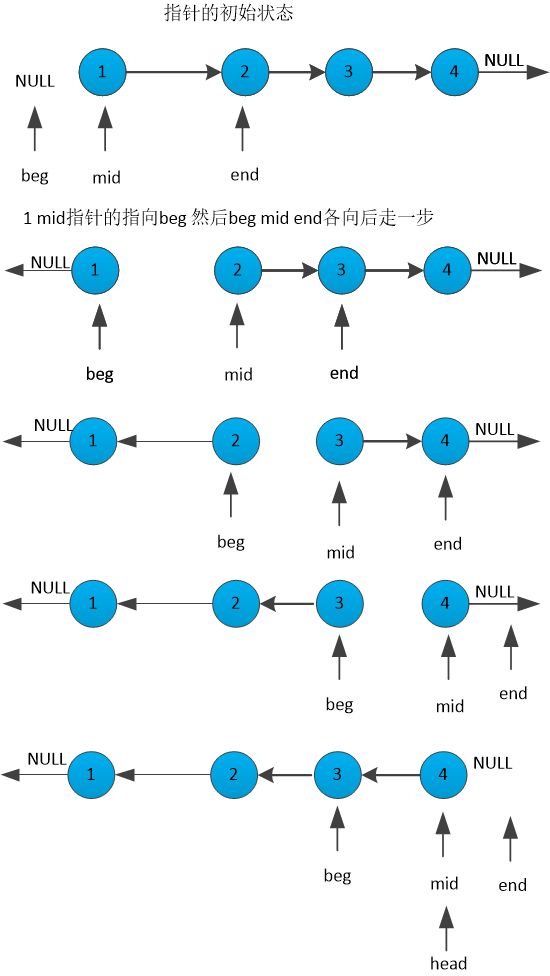
1) 使用迭代法反转链表
使mid指针指向beg end指针指向下一个节点 整个过程如下
coding
public static class Node<V> {
V e;
Node next;
Node(V data){
this.e = data;
}
}
/**
* 使用迭代法反转单向链表
* @param head
* @param
* @return
*/
public static <V> Node iteration_reverse(Node<V> head){
if (head == null || head.next == null){
return head;
}
Node beg = null;
// mid指针指向当前节点
Node mid = head;
// end 指向下一个节点
Node end = head.next;
while (true){
// 先把当前指针的指向修改为指向前一个节点
mid.next = beg;
// 到了最后一个节点退出
if (end == null){
break;
}
beg = mid;
mid = end;
end = end.next;
}
// 头结点指向当前节点
head = mid;
return head;
}
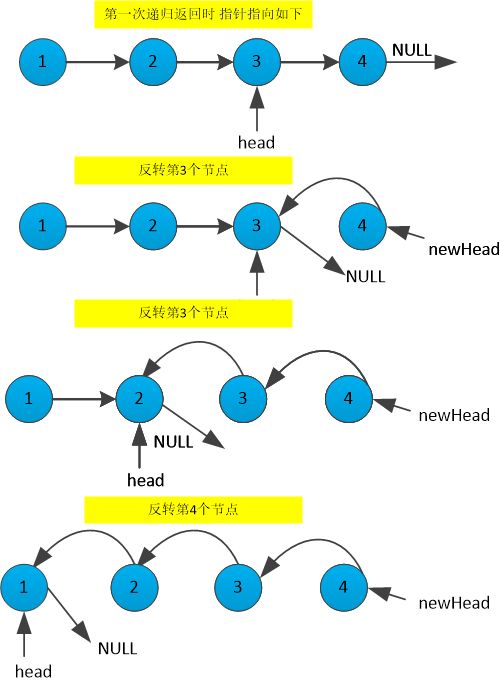
2) 使用递归的方式反转链表
递归反转链表可以理解成找到倒数第二个节点,把最后一个节点当成头返回,利用递归的压栈机制,依次对调用过程中的节点进行反转 其过程如下 :
/**
* 递归反转单向链表 每一次递归返回 head都是指向还未反转部分倒数第二个
* 然后把倒数第二个节点挂在已反转的链表上
* @param head
* @param
* @return
*/
public static <V> Node<V> recur_reverse(Node<V> head){
if (head == null || head.next == null){
return head;
} else {
// 一直往链表的最后一个节点找 找到倒数第二个节点返回
Node<V> newHead = recur_reverse(head.next);
// 上面一个返回的newHead是未反转的链表中的最后一个节点
// head是指向未反转部分的倒数第二个节点
// head.next.next 要反转的节点的next域
head.next.next = head;
head.next = null;
// 到此就把一个节点反转
return newHead;
}
}
coding
public static <V> Node<V> stack_reverse(Node<V> head){
if (head == null || head.next == null){
return head;
}
Stack<Node<V>> stack = new Stack<>();
// 先将单向链表中所有的节点都放入到栈中
while (head != null){
stack.push(head);
head = head.next;
}
Node<V> preNode = stack.pop();
head = preNode;
// 从栈中取出元素 构建一个单向链表
while (!stack.isEmpty()){
Node<V> node = stack.pop();
preNode.next = node;
preNode = node;
}
preNode.next = null;
return head;
}
3)使用头插法反转链表
/**
* 从单向链表的头开始 摘下一个节点 就放在已反转部分的头部
* @param head
* @param
* @return
*/
public static <V> Node<V> head_reverse(Node<V> head){
if (head == null || head.next == null){
return head;
}
Node<V> pre = null;
Node<V> next = null;
while (head != null){
// 先保存下一个节点
next = head.next;
// 摘下来的节点放在最前面
head.next = pre;
// 当前节点成为前一个节点
pre = head;
// 下一个节点
head = next;
}
return pre;
}
3 单向链表区间反转
将一个节点数为 size 链表 m 位置到 n 位置之间的区间反转,要求时间复杂度
O ( n ) O(n) O(n),空间复杂度 O ( 1 ) O(1) O(1)。
例如:
给出的链表为 1 → 2 → 3 → 4 → 5 → N U L L 1\rightarrow2\rightarrow3\rightarrow4\rightarrow5\rightarrow NULL 1→2→3→4→5→NULL, m = 2 m=2 m=2, n = 4 n=4 n=4,返回 1 → 4 → 3 → 2 → 5 → N U L L 1\rightarrow 4\rightarrow3\rightarrow2\rightarrow5\rightarrow NULL 1→4→3→2→5→NULL.
数据范围: 链表长度 0 ≤ s i z e ≤ 1000 0\leq{size}\leq1000 0≤size≤1000,链表中每个节点的值满足 ∣ v a l ∣ ≤ 1000 | val | \leq 1000 ∣val∣≤1000
要求时间复杂度 O ( n ) O(n) O(n) 空间复杂度 O ( 1 ) O(1) O(1)
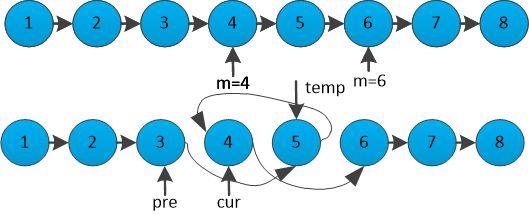
先遍历到反转区间的第一个元素,然后对区间元素进行反转
反转示意图如下 :
import java.util.*;
/*
* public class ListNode {
* int val;
* ListNode next = null;
* public ListNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类
* @param m int整型
* @param n int整型
* @return ListNode类
*/
public ListNode reverseBetween (ListNode head, int m, int n) {
if(head == null || head.next == null){
return head;
}
ListNode retNode = new ListNode(-1);
retNode.next = head;
ListNode pre = retNode;
ListNode cur = head;
// 先进行遍历 cur指针指向区间内的第一个节点
int i = 1;
while(i < m){
pre = cur;
cur = cur.next;
i++;
}
// pre 指针指向反转区间的前一个
// cur 指针指向当前的反转区间
// 一次循环反转区间的一个节点
for(i = m; i < n; i++){
// 保存 [m,n]区间要反转的节点 就是tempNode放在最前面
ListNode tempNode = cur.next;
// 当前节点直接指向下一个
cur.next = tempNode.next;
// 把tempNode挂在反转的最前面
tempNode.next = pre.next;
// 反转区间的前一个指针指向 tempNode 这样相当于把tempNode挪到最前面
pre.next = tempNode;
}
return retNode.next;
}
}
4 单向链表返回倒数k个节点问题
-
输入一个长度为 n n n 的链表,设链表中的元素的值为 a i a_i ai ,返回该链表中倒数第 k k k个节点。如果该链表长度小于 k k k,请返回一个长度为 0 0 0 的链表。
数据范围: 0 ≤ n ≤ 1 0 5 0\leq n\leq10^5 0≤n≤105 0 ≤ a i ≤ 1 0 9 0\leq{a_i}\leq10^9 0≤ai≤109
要求时间复杂度 O ( n ) O(n) O(n) 空间复杂度 O ( n ) O(n) O(n)
第一种解法 : 先求出整个链表的长度 i i i,在从头开始走 i − k i-k i−k步
coding
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
* @param pHead ListNode类
* @param k int整型
* @return ListNode类
*/
public static ListNode FindKthToTail (ListNode pHead, int k) {
if (pHead == null){
return null;
}
ListNode X = pHead;
ListNode Y = pHead;
// 先计算出单向链表的长度
int i = 0;
while (X != null){
++i;
X = X.next;
}
// 链表的长度小于k 直接返回null
if (i < k){
return null;
}
// 单向链表从头开始走 i - k步
for (int index = 0;index < i - k;index++){
Y = Y.next;
}
return Y;
}
第二种解法 : 快指针先走 k k k步,之后快慢指针一起走,快指针走到最后停
coding
/**
*
* @param pHead
* @param k
* @return
*/
public static ListNode FindKthToTail (ListNode pHead, int k) {
if (pHead == null){
return null;
}
// 慢指针
ListNode slow = pHead;
// 快指针
ListNode fast = pHead;
//因为fast指针最后是指向null的 所以快指针先走k步 之后各走一步
int i = 0;
for (;fast != null ; i++) {
fast = fast.next;
if (i >= k){
slow = slow.next;
}
}
return i < k ? null : slow;
}
测试部分代码
public static void test(){
ListNode head = new ListNode(0);
for (int i = 0;i < 10;++ i){
int val = (int) (Math.random() * 100);
addNode(head,val);
}
printListNode(head);
ListNode node = FindKthToTail1(head, 2);
printListNode(node);
}
public static class ListNode {
int val;
ListNode next = null;
public ListNode(int val) {
this.val = val;
}
}
public static ListNode addNode(ListNode head,int val){
ListNode tempNode = head;
while (tempNode.next != null){
tempNode = tempNode.next;
}
ListNode newNode = new ListNode(val);
tempNode.next = newNode;
newNode.next = null;
return head;
}
public static void printListNode(ListNode head){
if (head == null){
System.err.println(">>> head is null");
return;
}
ListNode p = head;
while (p != null){
System.out.print(p.val + " ");
p = p.next;
}
System.out.println();
}
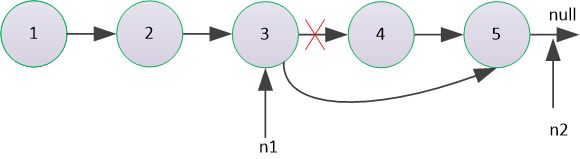
- 给定一个链表,删除链表的倒数第 n 个节点并返回链表的头指针
例如,给出的链表为: 1 → 2 → 3 → 4 → 5 1\rightarrow2\rightarrow3\rightarrow4\rightarrow5 1→2→3→4→5 n = 2 n=2 n=2
删除了链表的倒数第 n 个节点之后,链表变为
1 → 2 → 3 → 5 1\rightarrow2\rightarrow3\rightarrow5 1→2→3→5
数据范围: 链表长度 0 ≤ 0\leq 0≤n ≤ 1000 \leq1000 ≤1000,链表中任意节点的值满足 0 ≤ v a l u e ≤ 100 0\leq value \leq100 0≤value≤100
要求:空间复杂度 O ( 1 ) O(1) O(1),时间复杂度 O ( n ) O(n) O(n)
使用快慢指针,慢指针指向头结点的前一个节点,快指针指向第一个节点,快指针先走k不,快慢指针开始一起走,快指针走到最后,慢指针到要删除节点的前一个节点
图解
import java.util.*;
/*
* public class ListNode {
* int val;
* ListNode next = null;
* public ListNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类
* @param n int整型
* @return ListNode类
*/
public ListNode removeNthFromEnd (ListNode head, int n) {
// write code here
if(head == null || head.next == null ){
return null;
}
ListNode retNode = new ListNode(-1);
retNode.next = head;
ListNode n1 = head;
ListNode n2 = retNode;
// n1先走n步 n指向null时 n2指向要删除节点的前一个
int i = 0;
for(;n1 != null;i++){
if(i >= n){
n2 = n2.next;
}
n1 = n1.next;
}
n2.next = n2.next.next;
return retNode.next;
}
}
解法2 :
先求出链表的长度L,创建一个新的节点retNode将retNode赋值给临时节点node,node移动 L − k L - k L−k 步,此时node会来到要删除节点的前一个节点,修改node的指向即可
coding
import java.util.*;
/*
* public class ListNode {
* int val;
* ListNode next = null;
* public ListNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类
* @param n int整型
* @return ListNode类
*/
public ListNode removeNthFromEnd (ListNode head, int n) {
// write code here
if(head == null || head.next == null ){
return null;
}
ListNode retNode = new ListNode(-1);
retNode.next = head;
int i = 0;
ListNode node = head;
// 计算链表的长度
while(node != null) {
i ++;
node = node.next;
}
node = retNode;
// retNode走 iLen - n步
for(int k = 0; k < i - n;k++){
node = node.next;
}
/*
i = i - n;
while(i > 0){
i--;
node = node.next;
}*/
// cur指针会指向 iLen - n -1
node.next = node.next.next;
return retNode.next;
}
}
5 k个一组反转问题
将给出的链表中的节点每 k 个一组翻转,返回翻转后的链表如果链表中的节点数不是 k 的倍数,将最后剩下的节点保持原样你不能更改节点中的值,只能更改节点本身。
数据范围: 0 ≤ n ≤ 2000 0\leq n \leq 2000 0≤n≤2000 1 ≤ k ≤ 2000 1\leq k \leq2000 1≤k≤2000 链表中每个元素都满足 0 ≤ v a l ≤ 2000 0\leq val\leq2000 0≤val≤2000
要求空间复杂 O ( 1 ) O(1) O(1) 时间复杂度 O ( n ) O(n) O(n)
例如 给定的链表 是 1 → 2 → 3 → 4 → 5 1\rightarrow2\rightarrow3\rightarrow4\rightarrow5 1→2→3→4→5
对于 k = 2 k = 2 k=2 返回 2 → 1 → 4 → 3 → 5 2\rightarrow 1 \rightarrow4 \rightarrow3\rightarrow 5 2→1→4→3→5
对于 k = 3 k=3 k=3 返回 3 → 2 → 1 → 4 → 5 3\rightarrow2\rightarrow 1\rightarrow 4\rightarrow 5 3→2→1→4→5
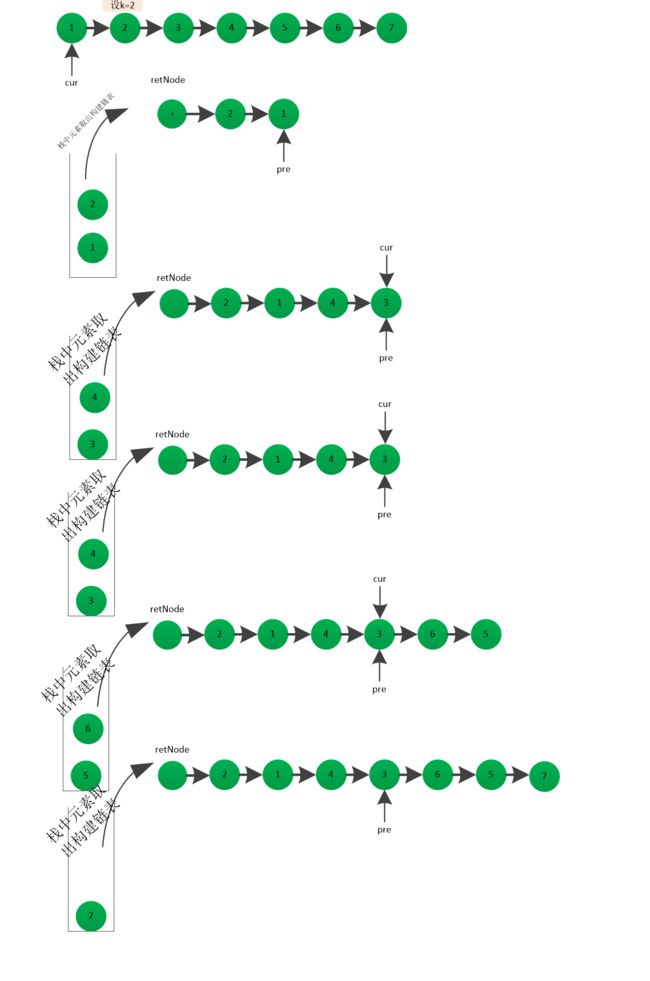
1) 使用栈进行反转
整体的思路1 : 遍历一次链表 当栈中有k个节点时 对k个节点进行反转;遍历完成之后,栈中没有节点,则不进行处理,如果栈中还有节点,则需要从栈中取出元素,保持顺序不变,挂在已反转的最后一个节点上
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类
* @param k int整型
* @return ListNode类
*/
public static ListNode reverseKGroup (ListNode head, int k) {
// write code here
ListNode cur = head;
Stack<ListNode> stack = new Stack<>();
// 要返回的节点
ListNode retNode = new ListNode(-1);
// 将这个要返回的节点设置为前一个节点
ListNode pre = retNode;
// 最终生成的单向链表的最后一个节点
ListNode lastNode = null;
for (int i = 1; cur != null;i++){
// 先保存下一个节点
ListNode next = cur.next;
stack.push(cur);
// 攒足了k个节点 则将这个k个节点进行反转
if (i % k == 0){
while (!stack.isEmpty()){
// 取出一个节点就挂在后面
ListNode node = stack.pop();
pre.next = node;
pre = node;
}
}
// 继续下一个节点
cur = next;
}
// 栈为空 节点个数就是k的整数倍 则说明没有节点了
if (stack.isEmpty()){
pre.next = null;
}
// 栈非空 就需要把栈中的元素取出和原来一样
while (!stack.isEmpty()){
ListNode node = stack.pop();
// 取出一个就挂在最前面 pre是指向已反转的最后一个节点
// 在整个循环的过程中 pre的位置不会动
pre.next = node;
// 取出的节点指向之前取出的节点 因为上一次取出的节点本来就应该在后面的
node.next = lastNode;
// 当前节点成为了最后一个节点
lastNode = node;
}
return retNode.next;
}
coding
import java.util.*;
/*
* public class ListNode {
* int val;
* ListNode next = null;
* public ListNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类
* @param k int整型
* @return ListNode类
*/
public ListNode reverseKGroup (ListNode head, int k) {
// write code here
ListNode retNode = new ListNode(-1);
retNode.next = head;
ListNode pre = retNode;
ListNode cur = head;
while(cur != null){
// 当前节点先走k-1步 判断当前节点是否到了链表的最后
ListNode tempNode = cur;
// 还未处理的节点的个数
int leftCount = 0;
for(; tempNode != null ;leftCount++){
// 剩余节点的个数大于等于k 则说明还够反转 直接退出
if(leftCount >= k){
break;
}
tempNode = tempNode.next;
}
if(leftCount >= k){ // 剩余的个数足够反转
// 反转组内的k个节点 循环k-1次
for(int i = 1;i < k;i++){
//先保存当前节点的下一个节点
ListNode next = cur.next;
// 当前节点跳过一个指
cur.next = next.next;
// 下一个节点next指向pre的指向
next.next = pre.next;
pre.next = next;
}
// 反转k个之后 当前的k就变成了pre
pre = cur;
// 执行完上一个循环 cur 往后走一步
cur = cur.next;
} else { // 不够则直接返回
return retNode.next;
}
}
return retNode.next;
}
}
6 链表回文问题
描述
给定一个链表,请判断该链表是否为回文结构。
回文是指该字符串正序逆序完全一致。
数据范围: 链表节点数
0 ≤ n ≤ 1 0 5 0≤n≤10^5 0≤n≤105 ,链表中每个节点的值满足 0 ≤ ∣ v a l ∣ ≤ 1 0 7 0≤∣val∣≤10^7 0≤∣val∣≤107
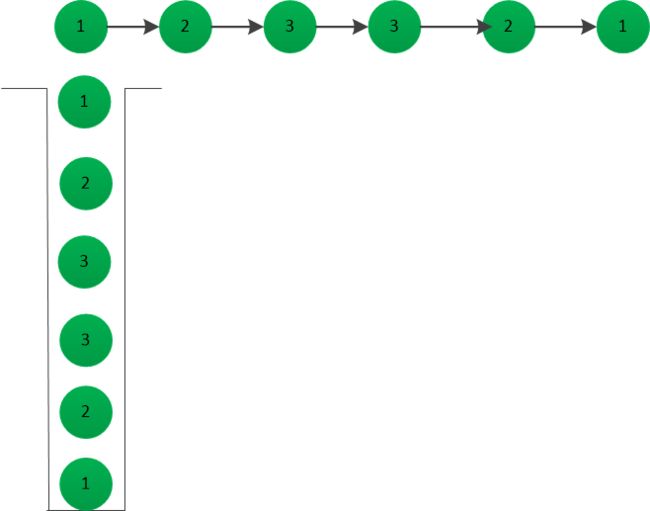
思路1 : 链表先栈,然后从头开始遍历链表,每次遍历都从栈中弹出一个元素与遍历的元素比较 不相等则不是
coding
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类 the head
* @return bool布尔型
*/
public static boolean isPail (ListNode head) {
// write code here
// 先做判断
if (head == null || head.next == null){
return true;
}
// 先将链表中的节点放入栈
ListNode tempNode = head;
Stack<ListNode> stack = new Stack<>();
while (tempNode != null){
stack.push(tempNode);
tempNode = tempNode.next;
}
tempNode = head;
// 遍历链表 从栈中弹出一个节点与之比较 不等直接返回false
while (!stack.isEmpty()){
ListNode listNode = stack.pop();
if (tempNode.val != listNode.val){
return false;
}
tempNode = tempNode.next;
}
return true;
}
以上其实是整张链表都进栈了,额外空间 O ( n ) O(n) O(n)
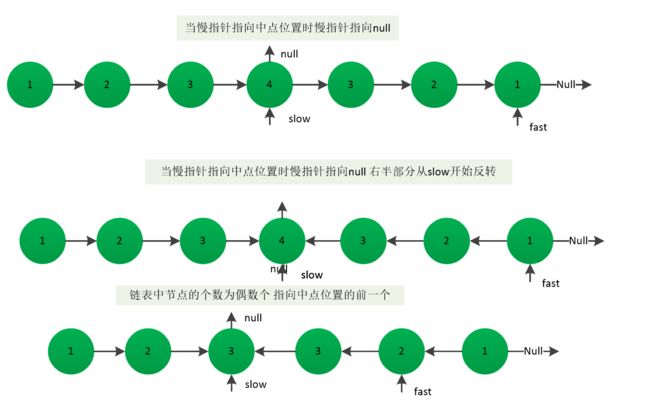
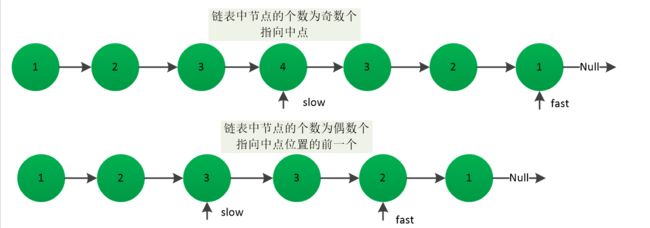
方法二 : 只是右边进栈,右边在栈非空的情况下,从栈中弹出节点和从头开始遍历的节点值进行比较,如果不等,直接返回false
下图分析了链表节点个数为奇数个和偶数个时,指针指向重点的情况
coding
import java.util.*;
/*
* public class ListNode {
* int val;
* ListNode next = null;
* public ListNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类 the head
* @return bool布尔型
*/
public boolean isPail (ListNode head) {
// write code here
if(head == null || head.next == null){
return true;
}
ListNode left = head;
ListNode right = head;
Stack<ListNode> stack = new Stack<>();
// right一次走两步 left一次走一步
// 当链表中的节点个数为奇数个时,left指针指向中点
// 当链表中的节点个数为偶数个时,left指针中点的前一个
while(right.next != null && right.next.next != null){
left = left.next;
right = right.next.next;
}
// 链表的右边部分进栈
while(left != null){
stack.push(left);
left = left.next;
}
left = head;
// 从栈中弹出元素和开头比较
while(!stack.isEmpty()){
if(left.val != stack.pop().val){
return false;
}
left = left.next;
}
return true;
}
}
前两种解法都使用到了额外的栈空间,那有没有不使用额外栈空间的方法的呢?
答案是 有
具体解法
1 先找到链表的中点位置 中点位置指向null 中点(包括)及以后的部分反转
2 然后两个一个从头开始遍历,一个指针尾部开始遍历 在遍历的过程中比较值,如果不相等,则不是回文结构
3 恢复链表结构
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类 the head
* @return bool布尔型
*/
public static boolean isPail1 (ListNode head) {
// write code here
// 先做判断
if (head == null || head.next == null){
return true;
}
// 慢指针
ListNode n1 = head;
// 快指针
ListNode n2 = head;
// 找链表中点的位置
while (n2.next != null && n2.next.next != null){
// 慢指针一次走一步
n1 = n1.next;
// 快指针一次走两步
n2 = n2.next.next;
}
// 需要反转部分的第一个节点 n2无用 在这个地方可以复用
n2 = n1.next;
// 中点位置指向 null n1其实可以当成反转部分的第一个节点
// n1 是反转链表中的前一个节点
n1.next = null;
// 完成了n1后面部分的反转
ListNode n3 = null;
while (n2 != null){
// 保存下一个节点
n3 = n2.next;
// 指向前一个节点
n2.next = n1;
// n2就成为了前一个节点
n1 = n2;
// 继续下一个节点
n2 = n3;
}
// 保存链表的最后一个节点
n3 = n1;
// n2指向尾部 没有用 可以复用
n2 = head;
// 两个指针 一个从头部开始 一个从尾部开始
boolean bIsPail = true;
while (n2 != null && n1 != null){
if (n2.val != n1.val){
bIsPail = false;
break;
}
// 头部往后走一个
n2 = n2.next;
// 尾部往后走一个
n1 = n1.next;
}
// n3链表的最后一个节点
n1 = n3.next;//保存前一个节点
// 已反转部分最前面的节点
n3.next = null;
// 把链表恢复
while (n1 != null) {
// 先保存下一个
n2 = n1.next;
// 指向已反转部分的最前面的节点
n1.next = n3;
// n1 成为已反转部分的最前面的节点
n3 = n1;
// 继续下一个节点
n1 = n2;
}
return bIsPail;
}
7 单向链表区间划分问题
给定一个单链表的头节点head,节点的值类型是整型,再给定一个整数pivot。实现一个调整链表的函数,将链表调整为左部分都是值小于pivot的节点,中间部分都是值等于pivot的节点,右部分都是值大于pivot的节点
方法1 : 1) 创建数组,把链表中的节点都放入到链表中
2) 在数组中对链表进行分区
3) 把分区的数据构建成链表
/**
* 给定一个单链表的头节点head,节点的值类型是整型,再给定一个整数pivot
* 实现一个调整链表的函数,将链表调整为左部分都是值小于pivot的节点,
* 中间部分都是值等于pivot的节点,右部分都是值大于pivot的节点
* @param head
* @param pivot
*/
public static ListNode listPartition(ListNode head,int pivot){
//先遍历链表,计算链表中节点的个数
if (head == null){
return head;
}
int i = 0;
ListNode n1 = head;
while (n1 != null){
n1 = n1.next;
++i;
}
// 创建ListNode数组
ListNode[] nodes = new ListNode[i];
ListNode cur = head;
for (i = 0;i < nodes.length;i++){
nodes[i] = cur;
cur = cur.next;
}
arrPartition(nodes,pivot);
for (i = 1; i < nodes.length;i++){
nodes[i - 1].next = nodes[i];
}
nodes[i-1].next = null;
return nodes[0];
}
public static void swap(ListNode[] nodes,int a,int b){
ListNode node = nodes[a];
nodes[a] = nodes[b];
nodes[b] = node;
}
public static void arrPartition(ListNode[] nodes,int pivot){
// 小于区域左边界
int less = -1;
// 大于区域右边界
int more = nodes.length;
int index = 0;
while (index < more)
if (nodes[index].val < pivot){//和小于区域的下一个做交换
swap(nodes,index++,++less);
} else if (nodes[index].val > pivot){ //和大于区域的前一个做交换
swap(nodes,index,--more);
} else {
index ++;
}
}
解法2 : 声明6个指针 :
小于部分的头
小于部分的尾
等于部分的头
等于部分的尾
大于部分的头
大于部分的尾
遍历一遍链表,在遍历的过程对链表节点的值和给定的值比较,分别加到不同的区域,最后将各个部分连接起来
public static ListNode listPartition2(ListNode head,int pivot){
//先遍历链表,计算链表中节点的个数
if (head == null){
return null;
}
ListNode sH = null; // 小于部分的头
ListNode sT = null;// 小于部分的尾
ListNode eH = null; // 等于部分的头
ListNode eT = null; // 等于部分的尾
ListNode bH = null;// 大于部分的头
ListNode bT = null; // 大于部分的尾
ListNode n = null;
while (head != null){
n = head.next;
// 挂上一个节点后 之后的节点为 null
head.next = null;
if (head.val < pivot){ // 小于
if (sH == null){ //第一次找到
sH = head;
sT = head;
} else {
sT.next = head;
sT = head;
}
} else if (head.val == pivot){ // 等于
if (eH == null){
eH = head;
eT = head;
} else {
eT.next = head;
eT = head;
}
}else { // 大于
if (bH == null){
bH = head;
bT = head;
} else {
bT.next = head;
bT = head;
}
}
head = n;
}
// 先讨论尾部
if (sT != null){ // 小于部分的尾部不是null
sT.next = eH;
// 等于部分的尾部
eT = eT == null ? sT : eT;
}
if (eT != null) { // 等于部分的尾部
eT.next = bH;
}
return sH != null ? sH : eH != null ? eH : bH;
}
8 判断链表是否有环
判断给定的链表中是否有环。如果有环则返回true,否则返回false。
数据范围:链表长度 0 ≤ n ≤ 10000 0 \leq n \leq 10000 0≤n≤10000,链表中任意节点的值满足 0 ≤ n ≤ 10000 0≤n≤10000 0≤n≤10000要求:空间复杂度 O ( 1 ) O(1) O(1),时间复杂度 O ( n ) O(n) O(n)
此题比较简单,使用快慢指针即可解决 但是要注意循环退出的条件
coding
public static boolean hasCycle(ListNode head) {
// 链表为空 或者只有一个节点 是不会存在环的
if (head == null || head.next == null){
return false;
}
ListNode slow = head;
ListNode fast = head;
boolean bHasCycle = false;
// 如果链表的节点个数是奇数个 fast就会指向倒数第二个 fast.next.next == null 循环退出
// 如果链表的节点个数是偶数个 fast就会指向最后一个节点 fast.next == null 循环退出
while (fast.next != null && fast.next.next != null){
slow = slow.next;
fast = fast.next.next;
if (slow == fast){
bHasCycle = true;
break;
}
}
return bHasCycle;
}
解法2 : 使用set进行判断
public boolean hasCycle(ListNode head) {
// 链表为空 或者只有一个节点 是不会存在环的
if (head == null || head.next == null) {
return false;
}
Set<ListNode> set = new HashSet<>();
while(head != null){
if(set.contains(head)){
return true;
}
set.add(head);
head = head.next;
}
return false;
}
9 复制含有随机指针的链表
class Node {
int value;
Node next;
Node rand;
Node(int val) {
value = val;
}
}
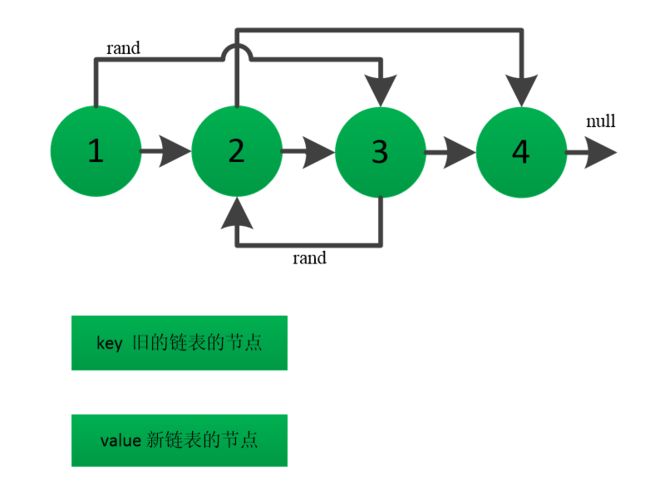
rand 指针是单链表节点结构中新增的指针,rand可能指向链表中的任意一个节点,也可能指向null。给定一个由Node节点类型组成的无环单链表的头节点head,请实现一个函数完成这个链表的复制,并返回复制的新链表的头节点。
第一种解法 :
- 创建一个map 遍历一次 单向链表,将节点作为key,创建一个新的节点作为value
- 再遍历单向链表,新链表的next指向旧链表的next指向的节点,这个节点从map中获取
coding
public static class Node{
int val;
Node next;
Node rand;
public Node(int val){
this.val = val;
}
}
public static Node copyList(Node head){
// key 旧的链表节点 value 新的链表节点
Map<Node,Node> nodeMap = new HashMap<>();
Node cur = head;
while (cur != null){
nodeMap.put(cur,new Node(cur.val));
cur = cur.next;
}
cur = head;
while (cur != null){
// 新的节点
Node newNode = nodeMap.get(cur);
// 新的next指针
newNode.next = nodeMap.get(cur.next);
// 新节点的rand指针
newNode.rand = nodeMap.get(cur.rand);
cur = cur.next;
}
return nodeMap.get(head);
}
解法2
不使用任何额外的数据结构
具体做法 :
1 遍历一次链表,每遍历到一个节点就复制,并直接挂在旧节点的后面
2 再遍历一次链表,每次取出新旧一对节点进行处理,设置旧的rand指针
3 将新旧混合在一起的链表拆分开来
coding
public static Node copyList1(Node head){
Node cur = head;
Node next = null;
while (cur != null){
next = cur.next;
// 创建一个新的节点挂在当前节点的后面
Node node = new Node(cur.val);
cur.next = node;
node.next = next;
cur = next;
}
cur = head;
Node curCpyNode = null;
while (cur != null){
// 先保存旧的下一个节点
next = cur.next.next;
// 当前复制的节点就是当前处理下一个节点
curCpyNode = cur.next;
// 当前拷贝节点的rand指针就是 当前处理节点的rand节点的下一个 如果有的话
curCpyNode.rand = cur.rand != null ? cur.rand.next : null;
// 继续处理下一个原节点
cur = next;
}
// 合并之后的链表进行拆分
cur = head;
Node ret = head.next;
while (cur != null){
next = cur.next.next;
curCpyNode = cur.next;
curCpyNode.next = next != null ? next.next : null;
cur = next;
}
return ret;
}
10 链表相交的一系列问题
1 第一个入环节点
给一个长度为n链表,若其中包含环,请找出该链表的环的入口结点,否则,返回null。
数据范围: n ≤ 10000 n \leq 10000 n≤10000 0 ≤ n o d e V a l u e ≤ 10000 0 \leq nodeValue \leq 10000 0≤nodeValue≤10000
要求时间复杂度 O ( n ) O(n) O(n) 空间复杂度 O ( 1 ) O(1) O(1)
解法1 : 使用set,在遍历单向链表的过程中去set中查找,如果可以找到,则当前的节点就是第一个入环节点,否则将当前节点放入set中
coding
/**
* 返回链表的第一个入环节点
* @param head
* @return
*/
public static ListNode EntryNodeOfLoop(ListNode head){
if (head == null || head.next == null){
return null;
}
Set<ListNode> nodeSet = new HashSet<>();
while (head != null){
if (nodeSet.contains(head)){
return head;
}
nodeSet.add(head);
head = head.next;
}
return null;
}
解法2 使用快慢指针 慢指针一次走一步 快指针一次走两步 如果链表有环 则快慢指针相遇时,慢指针原地不动,快指针回到开头,然后快慢指针各走一步,快慢指针再次相遇时的节点就是第一个入环接节点
coding
import java.util.*;
/*
public class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
*/
public class Solution {
public ListNode EntryNodeOfLoop(ListNode pHead) {
if (pHead == null || pHead.next == null || pHead.next.next == null) {
return null;
}
// n1->第二个节点
ListNode n1 = pHead.next;
// n2 ->第三个节点
ListNode n2 = pHead.next.next;
// 快慢指针相遇后退出
while (n1 != n2) {
// 链表中节点的个数 链表无环
if (n2.next == null || n2.next.next == null) {
return null;
}
n1 = n1.next;
n2 = n2.next.next;
}
// 执行到这一步,链表一定是有环
// 快指针回到开头 快慢指针各走一步
n2 = pHead;
while (n1 != n2) {
n1 = n1.next;
n2 = n2.next;
}
return n1;
}
}
2 两个无环链表的公共节点
输入两个无环的单向链表,找出它们的第一个公共结点,如果没有公共节点则返回空(注意因为传入数据是链表,所以错误测试数据的提示是用其他方式显示的,保证传入数据正确的)
数据范围: n ≤ 1000 n≤1000 n≤1000
要求:空间复杂度 O ( 1 ) O(1) O(1),时间复杂度 O ( n ) O(n) O(n)
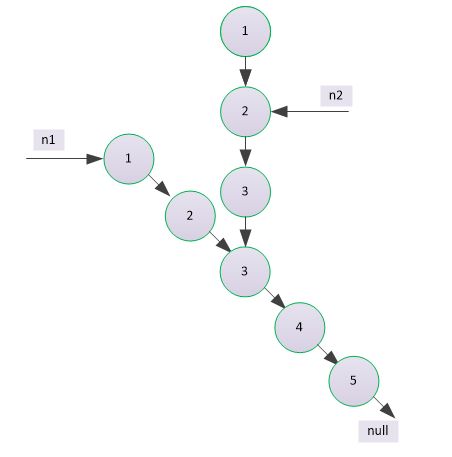
解题思路 :
遍历两条链表,分别得到两条链表的最后一个节点及两条链表中各自节点的个数 先看两条链表的最后一个节点的内存地址是否相等,不等直接返回null;等则长链表先走两条链表的差值步,再一起走,相遇时的节点即为第一个相交的节点
coding
import java.util.*;
/*
public class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}*/
public class Solution {
public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
if(pHead1 == null || pHead2 == null){
return null;
}
ListNode n1 = pHead1;
ListNode n2 = pHead2;
int n = 0;
// 循环结束后 n1来到 pHead1的最后一个节点
while(n1.next != null){
n ++;
n1 = n1.next;
}
// 循环结束后 n2来到 pHead2的最后一个节点
while(n2.next != null){
n --;
n2 = n2.next;
}
// 最后一个节点不等 一定不相交 直接返回 null
if (n1 != n2){
return null;
}
// 长链表
n1 = n > 0 ? pHead1 : pHead2;
// 短链表
n2 = n1 == pHead1 ? pHead2 : pHead1;
n = Math.abs(n);
// 长链表先走差值步
while(n != 0){
n --;
n1 = n1.next;
}
// 长短链表一起走
while(n1 != n2){
n1 = n1.next;
n2 = n2.next;
}
return n1;
}
}
单向链表一个有环一个无环,不可能相交
3 两个有环链表的公共节点
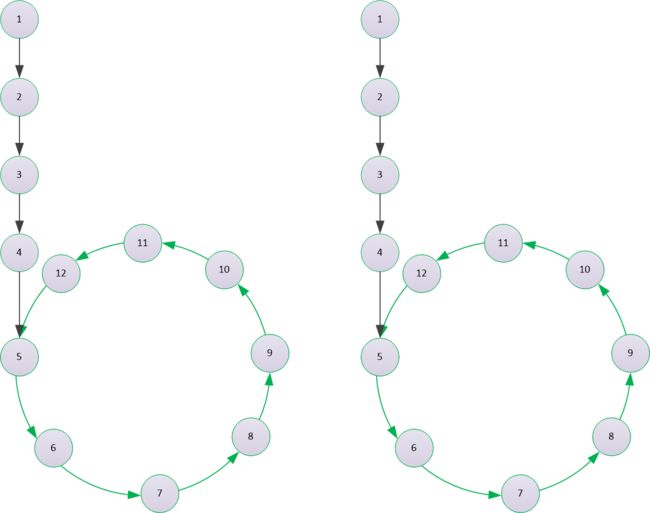
2) 在环外相交 (入环节点是同一个)
求公共的节点,可以看做是终止节点是入环节点的无环链表的相交问题
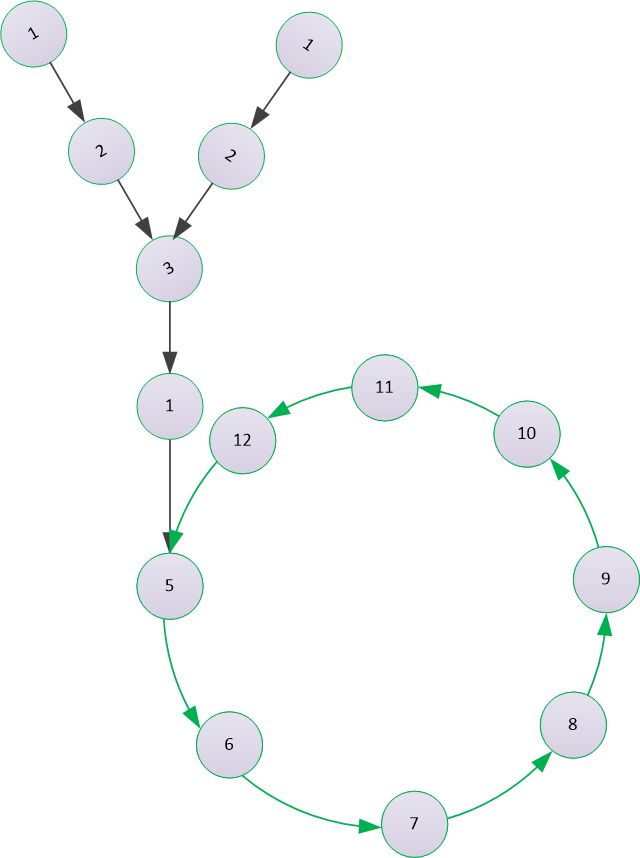
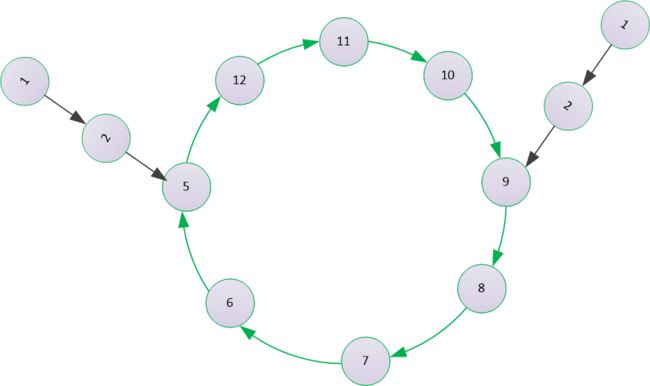
3) 在环上相交(入环节点不是同一个)
汇总
给定两个可能有环也可能无环的单链表,头节点head1和head2。请实现一个函数,如果两个链表相交,请返回相交的第一个节点。如果不相交,返回null
【要求】如果两个链表长度之和为N,时间复杂度请达到 O ( n ) O(n) O(n),额外空间复杂度请达到 O ( 1 ) O(1) O(1)。
/**
* 返回第一个入环节点
* @param head
* @return
*/
public static ListNode getLoopNode(ListNode head){
if (head == null || head.next == null || head.next.next == null) {
return null;
}
// n1->第二个节点
ListNode n1 = head.next;
// n2 ->第三个节点
ListNode n2 = head.next.next;
// 快慢指针相遇后退出
while (n1 != n2) {
// 链表中节点的个数 链表无环
if (n2.next == null || n2.next.next == null) {
return null;
}
n1 = n1.next;
n2 = n2.next.next;
}
// 执行到这一步,链表一定是有环
// 快指针回到开头 快慢指针各走一步
n2 = head;
while (n1 != n2) {
n1 = n1.next;
n2 = n2.next;
}
return n1;
}
/**
* 两个无环链表相交的节点
* @param head1
* @param head2
* @return
*/
public static ListNode noLoopNode(ListNode head1,ListNode head2){
if (head1 == null || head2 == null){
return null;
}
ListNode cur1 = head1;
ListNode cur2 = head2;
int n = 0;
// 循环退出时 cur1指向最后一个节点
while (cur1.next != null){
n ++;
cur1 = cur1.next;
}
// 循环退出时 cur2 指向 head2最后一个节点
while (cur2.next != null){
n --;
cur2 = cur2.next;
}
// 链表不相交
if (cur1 == cur2){
return null;
}
// 长链表
cur1 = n > 0 ? head1 : head2;
// 短链表
cur2 = cur1 == head1 ? head2 : head1;
// 长链表先走差值步
while (n != 0){
cur1 = cur1.next;
n --;
}
while (cur1 != cur2){
cur1 = cur1.next;
cur2 = cur2.next;
}
return cur1;
}
/**
* 两个有环链表相交的问题
* @param head1 第一条链表的头
* @param loop1 第一条链表的入环节点
* @param head2 第二条链表的头
* @param loop2 第二条链表的入环节点
* @return
*/
public static ListNode bothLoopNode(ListNode head1,ListNode loop1,ListNode head2,ListNode loop2){
ListNode n1 = head1;
ListNode n2 = head2;
if (loop1 == loop2){ // 两条链表的入环节点是同一个 两个无环链表的相交问题
int n = 0;
while (n1 != loop1){
n ++;
n1 = n1.next;
}
while (n2 != loop2){
n --;
n2 = n2.next;
}
// n1长链表
n1 = n > 0 ? head1 : head2;
// n2短链表
n2 = n1 == head1 ? n2 : head2;
// 长链表先走差值步
while (n > 0){
n1 = n1.next;
}
// 两个一起走
while (n1 != n2){
n1 = n1.next;
n2 = n2.next;
}
return n1;
} else { // 两个有环的链表在环内相交 相交节点不是同一个 或者不相交
// n1直接来到n1的入环节点的下一个
n1 = loop1.next;
// n1在回到自己过程中 如果能遇到loop2则n1就是公共节点
while (n1 != loop1) {
if ( n1 == loop2){
return loop1;
}
}
// 两个无环链表不相交
return null;
}
}
/**
* 给定两个可能有环也可能无环的单链表,
* 头节点head1和head2。请实现一个函数,
* 如果两个链表相交,请返回相交的第一个节点。
* 如果不相交,返回null
* @param pHead1
* @param pHead2
* @return
*/
public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
if (pHead1 == null || pHead2 == null){
return null;
}
// 分别求两条链表的入环节点
ListNode loop1 = getLoopNode(pHead1);
ListNode loop2 = getLoopNode(pHead2);
// 两个无环链表
if (loop1 == null && loop2 == null){
return noLoopNode(pHead1,pHead2);
}
// 一个有环 一个无环 单向链表不能相交
if ((loop1 == null && loop2 != null) || (loop2 == null && loop1 != null)){
return null;
}
// 两条链表都有环
if (loop1 != null && loop2 != null){
return bothLoopNode(pHead1,loop1,pHead2,loop2);
}
return null;
}
结语
链表的相关的小技巧
双指针 栈的使用
11 合并两个已排好序的链表
输入两个递增的链表,单个链表的长度为n,合并这两个链表并使新链表中的节点仍然是递增排序的。
数据范围: 0 < n < 1000 0< n<1000 0<n<1000 − 1000 < 节点值 < 1000 -1000 < 节点值 < 1000 −1000<节点值<1000
空间复杂度 O ( 1 ) O(1) O(1) 时间复杂度 O ( n ) O(n) O(n)
import java.util.*;
/*
* public class ListNode {
* int val;
* ListNode next = null;
* public ListNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pHead1 ListNode类
* @param pHead2 ListNode类
* @return ListNode类
*/
public ListNode Merge (ListNode pHead1, ListNode pHead2) {
// write code here
ListNode n1 = pHead1;
ListNode n2 = pHead2;
ListNode mergeHead = new ListNode(-1);
mergeHead.next = null;
ListNode pre = mergeHead;
while (n1 != null && n2 != null) {
if (n1.val < n2.val) {
pre.next = n1;
pre = n1;
n1 = n1.next;
} else {
pre.next = n2;
pre = n2;
n2 = n2.next;
}
}
while (n1 != null) {
pre.next = n1;
pre = n1;
n1 = n1.next;
}
while (n2 != null) {
pre.next = n2;
pre = n2;
n2 = n2.next;
}
return mergeHead.next;
}
}