必刷算法题之二分查找（题目及代码）---C++
本文给出的题目不限于二分查找，但是为了巩固二分查找的知识，只给出了二分查找的方法。
文章目录
-
- 第1题：二分查找（704）
- 第2题：猜数字大小
- 第3题：找出数组排序后的目标下标
- 第4题：搜索插入位置（35）
- 第5题：有效的完全平方数(367)
- 第6题：二维数组中的查找
- 第7题：x 的平方根
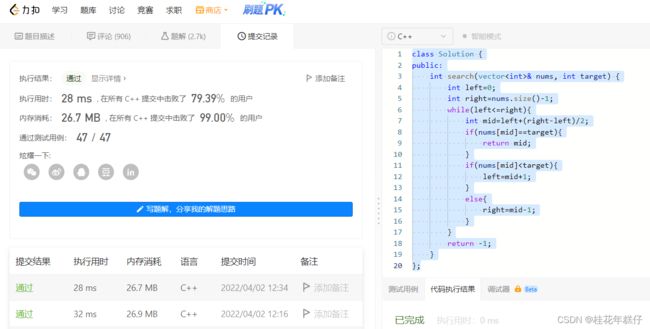
第1题：二分查找（704）
题目描述：
解题思路：
利用二分查找法：
- 先定义左右边界：即 left=0,right=nums.size()-1;
- 定义二分中值：mid=left+(right-left)/2; ? 为什么用这种，而不用mid=(left+right)/2，这是因为第二种有时候可能会出现越界的情况，比方说：int允许的最大值2147483647。 建议后面都用这种
- 如果mid位置的数等于目标值，直接返回结果
- 如果mid位置的数小于目标值，说明目标值在mid和right区间，那么重新定义左右区间和mid
- 如果mid位置的数大于目标值，说明目标值在mid和right区间，那么重新定义左右区间和mid
- 如果left>right说明找不到了，直接return -1。 值得注意的是要考虑输入一个数的情况，这和while中用的是 <= 还是 < 有关。
解题代码如下：
class Solution {
public:
int search(vector<int>& nums, int target) {
int left=0;
int right=nums.size()-1;
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]==target){
return mid;
}
if(nums[mid]<target){
left=mid+1;
}
else{
right=mid-1;
}
}
return -1;
}
};
时间和空间复杂度：
第2题：猜数字大小
题目描述：
有一说一，这个题目的中文描述看的我很迷，后面还是看英文的看懂了。英文描述如下：
解题思路：
这题目说了，有一个自带的函数int guess(num) 供你调用，参数是你猜测的数，返回值有三种情况，表示你猜对与否。那么这道题说白了就是一道隐式的二分数组查找题。
解题思路和上一题差不多，就是每一次更新了中间的数之后，要记得调用guess函数进行判断，不然会时间溢出。
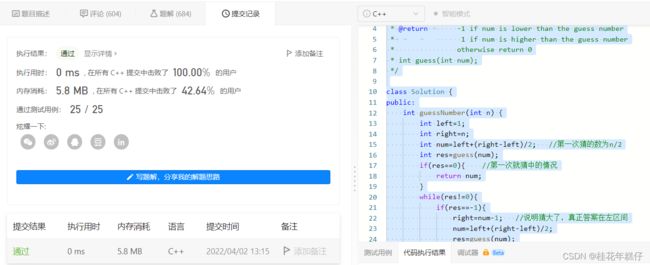
解题代码如下：
/**
* Forward declaration of guess API.
* @param num your guess
* @return -1 if num is lower than the guess number
* 1 if num is higher than the guess number
* otherwise return 0
* int guess(int num);
*/
class Solution {
public:
int guessNumber(int n) {
int left=1; //定义左区间
int right=n; //定义右区间
int num=left+(right-left)/2; //第一次猜的数为n/2
int res=guess(num); //调用函数查看猜测是否正确
if(res==0){ //第一次就猜中的情况
return num;
}
while(res!=0){
if(res==-1){
right=num-1; //说明猜大了，真正答案在左区间
num=left+(right-left)/2;
res=guess(num);
}
else{
left=num+1;
num=left+(right-left)/2;
res=guess(num);
}
}
return num;
}
};
时间和空间复杂度：
第3题：找出数组排序后的目标下标
题目描述：
解题思路：
为了用二分法这题前前后后花了我一个小时，吐血
- 首先对数组进行排序
- 然后用二分查找的方法找到target这个数，不管他的位置在哪
- 找到这个target的位置后往前找，一直找到他出现的第一个位置（这里要注意他是不是出现在下标为0的位置，因为往前查找需要下标位置-1，但是到0-1就会出现数组越界的情况，这时候需要判断）
- 找到第一个数后，把第一个数以及后面出现重复数值的下标给返回即可，直到下标中的数不等于target。
解题代码如下：
class Solution {
public:
vector<int> targetIndices(vector<int>& nums, int target) {
sort(nums.begin(),nums.end()); //先排序
vector<int> res;
if(nums.size()==1&&target==nums[0]){
res.push_back(0);
return res;
}
int left=0; //左区间
int right=nums.size()-1; //右区间
int mid=left+(right-left)/2;
while(left<=right){
if(nums[mid]==target){
while(nums[mid]==target){
mid=mid-1; //找到target的最小下标
if(mid==-1){
break;
}
}
if(mid==-1){
mid=0;
}
else{
mid=mid+1;
}
while(nums[mid]==target){
res.push_back(mid); //将下标存入数组中
mid=mid+1;
}
return res;
}
if(nums[mid]<target){ //说明目标值在左区间，则更新左边界
left=mid+1;
mid=left+(right-left)/2;
}
else{
right=mid-1;
mid=left+(right-left)/2;
}
}
return res;
}
};
时间和空间复杂度：
第4题：搜索插入位置（35）
题目描述：
解题思路：
这题可以分为两部分来做：**（1）对于存在于数组中的target，用二分法就能找到其位置。（2）**如果用二分法找不到的，就说明不在数组中，这时候left和right边界会重合，此时mid=left+(right-left)/2这三个点都重合，判断target和左边界的大小，如果比左边界大，那么就插在左边界的后面，即mid=mid+1；否则就直接插在这个重合点
解题代码如下：
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left=0;
int right=nums.size()-1;
int mid;
while(left<right){
mid=left+(right-left)/2;
if(nums[mid]==target){
return mid;
}else if(nums[mid]<target){
left=mid+1;
}else if(nums[mid]>target){
right=mid-1;
}
}
mid=left+(right-left)/2; //此时左右边界是重合的
if(target>nums[left]){
return mid+1;
}else{
return mid;
}
}
};
时间和空间复杂度：
第5题：有效的完全平方数(367)
题目描述：
解题思路：
由于题中num的范围很大，因此要注意int值是否会溢出，此外暴力搜索太费时间，还不能用库函数。
二分的思想就是判断当前的mid的平方是否=num。
解题代码如下：
class Solution {
public:
bool isPerfectSquare(int num) {
long long left=1,right=num;
while(left<=right){
long long mid=left+(right-left)/2;
if(num==mid*mid){
return true;
}else if(num>mid*mid){
left=mid+1;
}else if(num<mid*mid){
right=mid-1;
}
}
return false;
}
};
时间和空间复杂度：
第6题：二维数组中的查找
题目描述：
解题思路：
这里提一下暴力解法，因为涉及到二维数据，贴一下二维数组行列大小的表示方式。
class Solution {
public:
bool Find(int target, vector<vector<int> > array) {
for(int i=0;i<array.size();i++){ //array.size()表示二维数组的行数
for(int j=0;j<array[0].size();j++){ //array[0].size()表示二维数组的每行有多少列
if(array[i][j]==target){
return true;
}
}
}
return false;
}
};
二分查找法：
二维数组使用二分查找法和常规的一维数组不同，问题就在于如果第一行最后的一个数不一定小于第二行的第一个数。在牛客网看到一个高赞解题思路，很厉害，于是将他搬运过来了。
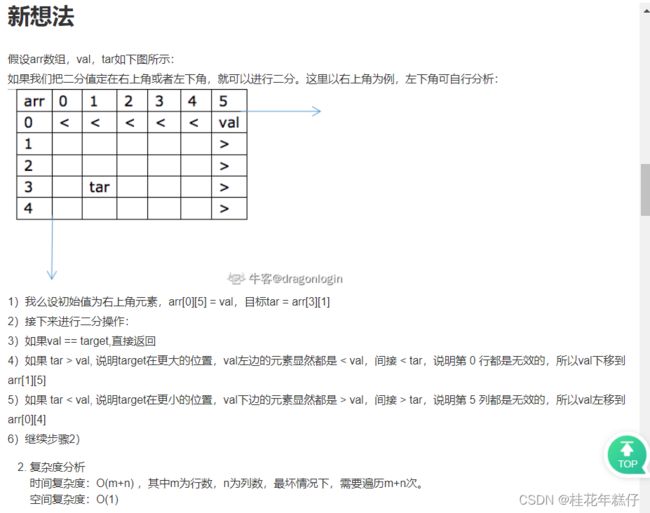
解题代码如下：
class Solution {
public:
bool Find(int target, vector<vector<int> > array) {
// 判断数组是否为空
int m = array.size(); //行大小
if (m == 0) return false;
int n = array[0].size(); //列大小
if (n == 0) return false;
int r = 0, c = n-1; // 右上角元素
while (r<m && c>=0) {
if (target == array[r][c]) {
return true;
}
else if (target > array[r][c]) {
++r; //移动至下一行
}
else {
--c; //向前一列移动
}
}
return false;
}
};
第7题：x 的平方根
题目描述：
解题思路：
假设 ans \textit{ans} ans是 x x x 平方根的整数部分，是满足 ans 2 ≤ x \textit{ans}^2 \leq x ans2≤x 的最大 整数值，因此我们可以对 ans \textit{ans} ans进行二分查找，从而得到答案。
二分查找的下界为 0，上界可以粗略地设定为 x x x 。在二分查找的每一步中，我们只需要比较中间元素 mid 2 \textit{mid}^2 mid2与 x x x的大小关系，并通过比较的结果调整上下界的范围。由于我们所有的运算都是整数运算，不会存在误差。
解题代码如下：
class Solution {
public:
int mySqrt(int x) {
int l = 0, r = x, ans = -1;
while (l <= r) {
int mid = l + (r - l) / 2;
if ((long long)mid * mid <= x) {
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return ans;
}
};
导航链接：必刷算法题—排序篇（C++）
导航链接：必刷算法题—哈希篇(C++)
导航链接：剑指—动态规划篇（C++）
导航链接：剑指—链表篇（C++）
导航链接：剑指—队列&栈篇（C++）
导航链接：剑指—树篇（C++）
注： 以上题目都是在牛客网或是leetcode中刷的，有自己做的，也有不会做看别人精华解题思路，然后总结的。如果侵犯了您的权益，请私聊我。
最后，觉得本文内容对你有所帮助的话，感谢您能点赞收藏，在我的剑指offer专栏还有相关的算法刷题文章，等待您的阅读！