冒泡、选择、插入、希尔、快速。基数排序---C语言版本
选择排序
什么是选择排序?
1、首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
2、再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
3、重复第二步,直到所有元素均排序完毕。
演示
假设有这样一个数组:
int sum[9]={2,5,8,1,7,4,3,9,6};
我们首先需要找到整个数组里面最小的哪一个元素。
假设第一个元素2为最小元素,我们开始往后比,当遍历到第四个元素时
候遇到比2小的数1.那么我们暂将1记做最小数并保存其下标,接着往后比
发现没有比1还要小的数了。那么此时1就是最小的那个元素。然后我们根
据保存的下标将2和1的位置互换就是:
1 ,5 ,8 ,2 ,7 ,4 ,3 ,9 ,6
然后我们开始找第二小的元素,此时我们假设第二个元素5为第二小元
素,开始往后遍历,遇到比5小的记录下标。我们遇到了2,往后发现没有
比2小的元素,那么2和5就交换位置。就这样一次次找下去!
代码
#include 快速排序
什么是快速排序?
1、 首先在数组中找一个元素做基准,通常选择第一个元素为基准
2、将比这个基准大的数移到这个基准的右边,比这个基准小的数移动到左边
3、经过2后,在这个基准左边和右边分别分别重复1、2步骤
演示:
假如有这样一个数组:sum[9]={2,3,8,7,1,5,4,6,9};
我们可以知道:sum[0]=2; sum[8]=9;
定义这两个下标:
int begin = 0 //数组起始下标
int end = 8 //数组结束下标
2 3 8 7 1 5 4 6 9
begin end
我们在定义一个基准,我就选择第一个元素为基准 int tmp = 2;
我们要实现比基准大的数据在基准左边,基准小的数据在基准左边
首先从end向左遍历,寻找比2小的数据,遍历到1的时候,1<2将1填入
sum[0],这时候数组就变成:
1 3 8 7 1 5 4 6 9
begin end
然后begin向右遍历,遇到比2大的数据放到end现在的位置上,遍历到3
就比2大,于是将3填写到end所处的位置上,现在这个数组就变成了:
1 3 8 7 3 5 4 6 9
begin end
然后end就又开始向左遍历寻找比2小的数据,当end遍历到begin位置时候,说明第一次遍历已经成功了,比基准大的数据都在基准右边,比基准小的数据都在基准左边。此时将基准的代表的元素填入此时begin和end的位置,这时候数组就是:
1 2 8 7 3 5 4 6 9
begin
end
{1} 2 {8 7 3 5 4 6 9}
接下来就是重复了,我们在2的右边比基准大的数组中在取一个基准,还是同样的遍历。 2的左边还是一样操作。
我们看一下重复部分代码实现
int temp = arr[begin];
int i = begin;
int j = end;
//不重复遍历
while(i < j)
{
//从右往左遍历寻找比基准小的数据
while(i<j && arr[j] > temp)//注意i=j时候
{
j--;
}
arr[i] = arr[j];
//从左往右遍历寻找比基准大的数据
while(i<j && arr[i] <= temp)//注意i=j时候
{
i++;
}
arr[j] = arr[i];
}
arr[i] = temp;//基准存入,此时i=j
完整源码:
#include "stdio.h"
#include "stdlib.h"
void quickSort(int *arr,int begin,int end);
int main()
{
int sum[9]={2,3,8,7,1,5,4,6,9};
quickSort(sum,0,8);
for(int i=0;i<9;i++)
{
printf("%d ",sum[i]);
}
printf("\n");
return 0;
}
void quickSort(int *arr,int begin,int end)
{
if(begin < end)
{
int temp = arr[begin];
int i = begin;
int j = end;
while(i < j)
{
while(i<j && arr[j] > temp)
j--;
arr[i] = arr[j];
while(i<j && arr[i] <= temp)
i++;
arr[j] = arr[i];
}
arr[i] = temp;
quickSort(arr,begin,i-1);//左区间
quickSort(arr,i+1,end);//右区间
}
else
return;
}
冒泡排序
什么是冒泡排序?
1、 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
2、对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
3、针对所有的元素重复以上的步骤,除了最后一个。
4、持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
#include插入排序
什么是插入排序?
1、将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
2、从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
演示:
有这样一个数组:sum[9]={4,7,1,2,9,5,6,3,8};
4 7 1 2 9 5 6 3 8
我们从第一个元素7开始,4<7所以不用移动,1<7
所以我们将1放到4的位置,4用一个变量占存。然后7移动到1的位置,4移动到7的位置这就变成了
1 4 7 2 9 5 6 3 8
然后到2了,2放到4的位置,4用变量暂存,7移动到2的位置,4移动到7的位置。
1 2 4 7 9 5 6 3 8
........
........
........
重复以上步骤即可,这样看可能还是有点绕直接上图:
3~9整体后移一位,空出一个空,2放入
代码
//原理很简单,代码理解起来可能稍微有点绕了
#include "stdio.h"
#include "stdlib.h"
void swap(int *a,int *b);
void insertion_sort(int arr[], int len);
int main()
{
int sum[9]={4,7,1,2,9,5,6,3,8};
insertion_sort(sum,9);
for(int i=0;i<9;i++)
{
printf("%d ",sum[i]);
}
return 0;
}
void insertion_sort(int arr[], int len)
{
int i,j,key;
for (i=1;i<len;i++)
{
key=arr[i]
j=i-1;
while(j>=0&&a[j]>key)
{
a[j+1]=a[j];
j--;
}
}
}
希尔排序
什么是希尔排序?
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
2、希尔排序是基于插入排序的以下两点性质而提出改进方法的:
3、插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率;
但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位;
4、希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
演示
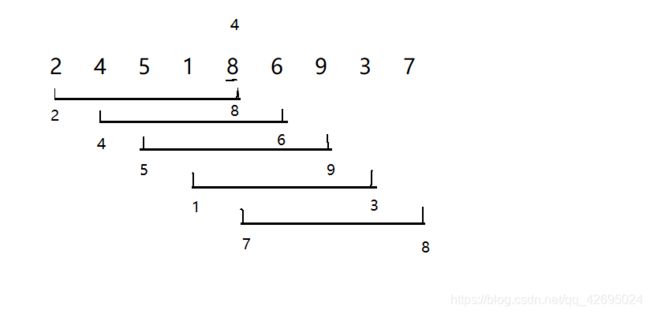
有这样一个数组: int sum[9]={2,4,5,1,8,6,9,3,7};
首先我们需要给这个数组划分成多个子序列。哪要划分多少个序列呢?
可以发现这个数组里面有9个元素!我们可以遵从这个序列划分方法。
序列个数=偶数个元素/2
序列个数=(奇数个元素+1)/2
简单点写法可以这样表达:n=元素个数>>1
示例:9>>1=4,10>>1=5,可能会问这不对啊,9是奇数啊,这样得到的是4不是5啊,但是数组下标是从0开始的,4下标不对应5个元素嘛!这样划分刚好每个元素都遍历到,划分的子序列个数也为5
我们这里有9个元素,;所以我们从数组下标4开始划分序列,也就是第五个元素
从8开始划分序列,如果2>8则交换位置,如果4>6则交换位置....
要注意一定要把每个元素都遍历到,可以看到上图只有7和8的位置需要
交换。这一次排序下来结果是不是就是:
2 4 5 1 7 6 9 3 8
这并没有排序完成,注意到开始我们是以4为序列开始的,是不是没有排
序完成,我们还要接着划分序列,给序列长度搞小一点,这样序列个数
不就多了嘛,不就排序更完善了嘛,我们上次是以9>>1=4来做的。这次我
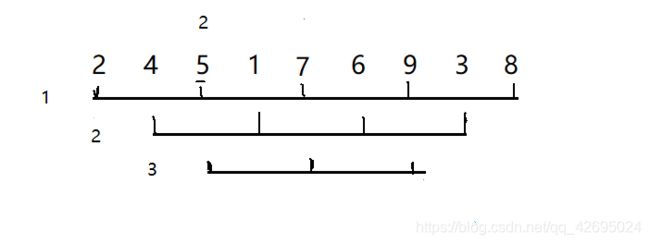
们就以4>>1=2来做.划分成3个序列
在1排序完成后我们可以得到
2 4 5 1 7 6 9 3 8
2排序完可以得到(注意2排序完成在1排序完的基础上)
2 1 5 3 7 4 9 6 8
3排序完我们可以得到(在2排序完的基础上)
2 1 5 3 7 4 8 6 9
这还没有排序完成,我们在2>>1划分成1个序列在排序,这里为啥是1个序
列呢?原因是没法在分了啊,1下标前面就是0下标,一次就保证所有元素
都遍历到,就不需要在分序列了。
1 2 5 3 7 4 8 6 9 1 2 比较
1 2 5 3 7 4 8 6 9 1 2 5 比较
1 2 3 5 7 4 8 6 9 1 2 5 3 比较
1 2 3 5 7 4 8 6 9 ......
1 2 3 4 5 7 8 6 9 ......
1 2 3 4 5 7 8 6 9 ......
1 2 3 4 5 6 7 8 9 1 2 3 4 5 7 8 6 比较
1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 比较
代码:
#include "stdio.h"
#include "stdlib.h"
void hill_config(int sum[],int len);
int main(void)
{
int sum[9]={2,4,5,1,8,6,9,3,7};
int a=9,b=0;
b=a>>1;
printf("%d\n",b);
hill_config(sum,9);
for(int i=0;i<9;i++)
{
printf("%d ",sum[i]);
}
return 0;
}
void hill_config(int arr[],int len)
{
int gap, i, j;
int temp;
for (gap = len >> 1; gap > 0; gap >>= 1)
{
printf("gap=%d\n",gap);
for (i = gap; i < len; i++)
{
temp = arr[i];
for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
{
arr[j + gap] = arr[j];
}
arr[j + gap] = temp;
}
}
}
参考:菜鸟教程