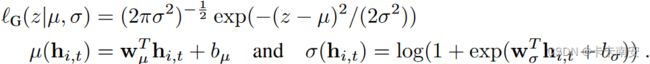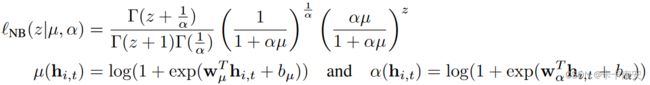【阅读笔记】概率预测之DeepAR(含Pytorch代码实现)
本文作为自己阅读论文后的总结和思考,不涉及论文翻译和模型解读,适合大家阅读完论文后交流想法,关于论文翻译可以查看参考文献。论文地址:https://arxiv.org/abs/1704.04110
DeepAR
-
- 一. 全文总结
- 二. 研究方法
- 三. 结论
- 四. 创新点
- 五. 思考
- 六. 参考文献
- 七. Pytorch实现⭐
-
- util(工具函数)
- Model
- Load Data
- Train
- Test
一. 全文总结
本文中提出了DeepAR,一种产生准确概率预测的方法,基于在大量相关时间序列上训练一个自回归递归网络模型。本文展示了如何通过将深度学习技术应用于概率预测,克服广泛使用的经典方法面临的许多挑战。通过对几个真实世界预测数据集的广泛经验评估,表明与最先进的方法相比,准确性提高了15%左右。
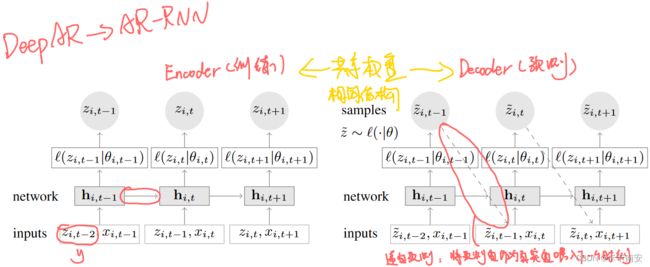
二. 研究方法
- 首先假设预测数据的分布情况,例如对于连续数据假设其分布为高斯分布,对于计数数据假设其为负二项分布,针对其他类型数据有其对应的分布。
- 提出了一种用于概率预测的RNN架构,预测预测值分布的参数,通过最小化负对数似然函数来更新模型参数。
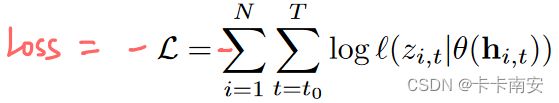
值得注意的是,在实验时由于编码器模型与解码器相同,在计算损失时包括了训练的历史序列,即 t 0 t_0 t0=0。
- 针对多时序尺度不一致的问题,引入尺度因子来调节尺度;针对不同尺度的时序数量不一致的问题,基于尺度因子在训练时进行非均匀采样。
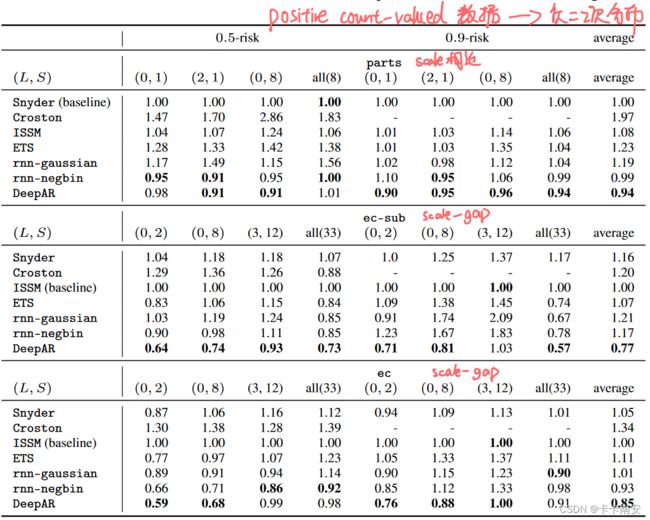
模型的预测性能如下表所示,三个数据集均为计数数据(positive count-valued),采用负二项分布的假设是更准确的,因此rnn-gaussian性能很差。rnn-negbin和DeepAR的差别就是有没有采用尺度因子和非均匀采样,可以看到在数据中没有scale-gap的数据集中二者的性能相近,在scale-gap数据集中DeepAR性能最优。
三. 结论
基于现代深度学习技术的预测方法可以在各种数据集上大大提高最先进的预测方法的预测精度。我们提出的DeepAR模型有效地从相关的时间序列中学习全球模型,通过尺度因子缩放和基于尺度的非均匀采样处理序列中尺度不一致的问题,以高精度生成校准概率预测,并能够从数据中学习复杂的模式,如季节性和不确定性随时间的增长。
四. 创新点
- 与传统RNN相比,本文预测每个时间点的概率分布参数从而获得每个时间点的概率密度函数,通过极大似然的方法来优化模型参数。
- DeepAR以蒙特卡罗样本的形式进行概率预测,该样本可用于计算预测视界内所有子范围的一致分位数估计。
- 对于多时序尺度不一致的问题,传统的方法是在数据预处理时标准化或者分组预测,本文采用引入尺度因子和非均匀加权采样的方法来解决这个问题。
- 支持直接输入多重时间序列,并且可以通过Embedding层来学习同类时间序列的共性,方便处理海量时间序列,并且能够处理序列中存在缺失值时的预测问题。
五. 思考
DeepAR属于是将深度学习与概率预测结合的一个突破,然而DeepAR属于概率预测中的参数预测,对预测值分布的提前假设会预测精度会产生极大影响。
六. 参考文献
- DeepAR:自回归循环网络进行时序概率进行预测
- 【时序】DeepAR 概率预测模型论文笔记
- [论文精读] DeepAR:使用自回归RNN预测时序概率分布⭐
七. Pytorch实现⭐
以下代码参考:https://github.com/jingw2/demand_forecast,修正了原代码中存在的一些错误,附添加了一些必要的注释让大家更好理解。
import torch
from torch import nn
import torch.nn.functional as F
from torch.optim import Adam
import numpy as np
import math
import os
import random
import matplotlib.pyplot as plt
import pickle
from tqdm import tqdm
import pandas as pd
from sklearn.preprocessing import StandardScaler
from datetime import date
import argparse
from progressbar import *
util(工具函数)
def get_data_path():
folder = os.path.dirname(__file__)
return os.path.join(folder, "data")
def RSE(ypred, ytrue):
rse = np.sqrt(np.square(ypred - ytrue).sum()) / \
np.sqrt(np.square(ytrue - ytrue.mean()).sum())
return rse
def quantile_loss(ytrue, ypred, qs):
'''
Quantile loss version 2
Args:
ytrue (batch_size, output_horizon)
ypred (batch_size, output_horizon, num_quantiles)
'''
L = np.zeros_like(ytrue)
for i, q in enumerate(qs):
yq = ypred[:, :, i]
diff = yq - ytrue
L += np.max(q * diff, (q - 1) * diff)
return L.mean()
def SMAPE(ytrue, ypred):
ytrue = np.array(ytrue).ravel()
ypred = np.array(ypred).ravel() + 1e-4
mean_y = (ytrue + ypred) / 2.
return np.mean(np.abs((ytrue - ypred) \
/ mean_y))
def MAPE(ytrue, ypred):
ytrue = np.array(ytrue).ravel() + 1e-4
ypred = np.array(ypred).ravel()
return np.mean(np.abs((ytrue - ypred) \
/ ytrue))
def train_test_split(X, y, train_ratio=0.7):
'''
- X (array like): shape (num_samples, num_periods, num_features)
- y (array like): shape (num_samples, num_periods)
'''
num_ts, num_periods, num_features = X.shape
train_periods = int(num_periods * train_ratio)
random.seed(2)
Xtr = X[:, :train_periods, :]
ytr = y[:, :train_periods]
Xte = X[:, train_periods:, :]
yte = y[:, train_periods:]
return Xtr, ytr, Xte, yte
class StandardScaler:
def fit_transform(self, y):
self.mean = np.mean(y)
self.std = np.std(y) + 1e-4
return (y - self.mean) / self.std
def inverse_transform(self, y):
return y * self.std + self.mean
def transform(self, y):
return (y - self.mean) / self.std
class MaxScaler:
def fit_transform(self, y):
self.max = np.max(y)
return y / self.max
def inverse_transform(self, y):
return y * self.max
def transform(self, y):
return y / self.max
class MeanScaler:
def fit_transform(self, y):
self.mean = np.mean(y)
return y / self.mean
def inverse_transform(self, y):
return y * self.mean
def transform(self, y):
return y / self.mean
class LogScaler:
def fit_transform(self, y):
return np.log1p(y)
def inverse_transform(self, y):
return np.expm1(y)
def transform(self, y):
return np.log1p(y)
def gaussian_likelihood_loss(z, mu, sigma):
'''
Gaussian Liklihood Loss
Args:
z (tensor): true observations, shape (num_ts, num_periods)
mu (tensor): mean, shape (num_ts, num_periods)
sigma (tensor): standard deviation, shape (num_ts, num_periods)
likelihood:
(2 pi sigma^2)^(-1/2) exp(-(z - mu)^2 / (2 sigma^2))
log likelihood:
-1/2 * (log (2 pi) + 2 * log (sigma)) - (z - mu)^2 / (2 sigma^2)
'''
negative_likelihood = torch.log(sigma + 1) + (z - mu) ** 2 / (2 * sigma ** 2) + 6
return negative_likelihood.mean()
def negative_binomial_loss(ytrue, mu, alpha):
'''
Negative Binomial Sample
Args:
ytrue (array like)
mu (array like)
alpha (array like)
maximuze log l_{nb} = log Gamma(z + 1/alpha) - log Gamma(z + 1) - log Gamma(1 / alpha)
- 1 / alpha * log (1 + alpha * mu) + z * log (alpha * mu / (1 + alpha * mu))
minimize loss = - log l_{nb}
Note: torch.lgamma: log Gamma function
'''
batch_size, seq_len = ytrue.size()
likelihood = torch.lgamma(ytrue + 1. / alpha) - torch.lgamma(ytrue + 1) - torch.lgamma(1. / alpha) \
- 1. / alpha * torch.log(1 + alpha * mu) \
+ ytrue * torch.log(alpha * mu / (1 + alpha * mu))
return - likelihood.mean()
def batch_generator(X, y, num_obs_to_train, seq_len, batch_size):
'''
Args:
X (array like): shape (num_samples, train_periods, num_features)
y (array like): shape (num_samples, train_periods)
num_obs_to_train (int): 训练的历史窗口长度
seq_len (int): sequence/encoder/decoder length
batch_size (int)
'''
num_ts, num_periods, _ = X.shape
if num_ts < batch_size:
batch_size = num_ts
t = random.choice(range(num_obs_to_train, num_periods-seq_len)) # 从num_obs_to_train和num_periods-seq_len-1之间随机选一个整数,作为预测点
batch = random.sample(range(num_ts), batch_size) # 从num_ts条数据中随机选择batch_size条
X_train_batch = X[batch, t-num_obs_to_train:t, :] # (batch_size, num_obs_to_train, num_features)
y_train_batch = y[batch, t-num_obs_to_train:t] # (batch_size, num_obs_to_train)
Xf = X[batch, t:t+seq_len, :] # (batch_size, seq_len, num_features)
yf = y[batch, t:t+seq_len] # (batch_size, seq_len)
return X_train_batch, y_train_batch, Xf, yf
Model
class Gaussian(nn.Module):
def __init__(self, hidden_size, output_size):
'''
Gaussian Likelihood Supports Continuous Data
Args:
input_size (int): hidden h_{i,t} column size
output_size (int): embedding size
'''
super(Gaussian, self).__init__()
self.mu_layer = nn.Linear(hidden_size, output_size)
self.sigma_layer = nn.Linear(hidden_size, output_size)
# initialize weights
# nn.init.xavier_uniform_(self.mu_layer.weight)
# nn.init.xavier_uniform_(self.sigma_layer.weight)
def forward(self, h): # h为神经网络隐藏层输出 (batch, hidden_size)
_, hidden_size = h.size()
sigma_t = torch.log(1 + torch.exp(self.sigma_layer(h))) + 1e-6
mu_t = self.mu_layer(h)
return mu_t, sigma_t # (batch, output_size)
class NegativeBinomial(nn.Module):
def __init__(self, input_size, output_size):
'''
Negative Binomial Supports Positive Count Data
Args:
input_size (int): hidden h_{i,t} column size
output_size (int): embedding size
'''
super(NegativeBinomial, self).__init__()
self.mu_layer = nn.Linear(input_size, output_size)
self.sigma_layer = nn.Linear(input_size, output_size)
def forward(self, h): # h为神经网络隐藏层输出 (batch, hidden_size)
_, hidden_size = h.size()
alpha_t = torch.log(1 + torch.exp(self.sigma_layer(h))) + 1e-6
mu_t = torch.log(1 + torch.exp(self.mu_layer(h)))
return mu_t, alpha_t # (batch, output_size)
def gaussian_sample(mu, sigma):
'''
Gaussian Sample
Args:
ytrue (array like)
mu (array like) # (num_ts, 1)
sigma (array like): standard deviation # (num_ts, 1)
gaussian maximum likelihood using log
l_{G} (z|mu, sigma) = (2 * pi * sigma^2)^(-0.5) * exp(- (z - mu)^2 / (2 * sigma^2))
'''
# likelihood = (2 * np.pi * sigma ** 2) ** (-0.5) * \
# torch.exp((- (ytrue - mu) ** 2) / (2 * sigma ** 2))
# return likelihood
gaussian = torch.distributions.normal.Normal(mu, sigma)
ypred = gaussian.sample()
return ypred # (num_ts, 1)
def negative_binomial_sample(mu, alpha):
'''
Negative Binomial Sample
Args:
ytrue (array like)
mu (array like)
alpha (array like)
maximuze log l_{nb} = log Gamma(z + 1/alpha) - log Gamma(z + 1) - log Gamma(1 / alpha)
- 1 / alpha * log (1 + alpha * mu) + z * log (alpha * mu / (1 + alpha * mu))
minimize loss = - log l_{nb}
Note: torch.lgamma: log Gamma function
'''
var = mu + mu * mu * alpha
ypred = mu + torch.randn() * torch.sqrt(var)
return ypred
class DeepAR(nn.Module):
def __init__(self, input_size, embedding_size, hidden_size, num_layers, lr=1e-3, likelihood="g"):
super(DeepAR, self).__init__()
# network
self.input_embed = nn.Linear(1, embedding_size)
self.encoder = nn.LSTM(embedding_size+input_size, hidden_size, \
num_layers, bias=True, batch_first=True)
if likelihood == "g":
self.likelihood_layer = Gaussian(hidden_size, 1)
elif likelihood == "nb":
self.likelihood_layer = NegativeBinomial(hidden_size, 1)
self.likelihood = likelihood
def forward(self, X, y, Xf):
'''
Args:
num_time_series = batch_size
X (array like): shape (num_time_series, num_obs_to_train, num_features)
y (array like): shape (num_time_series, num_obs_to_train)
Xf (array like): shape (num_time_series, seq_len, num_features)
Return:
mu (array like): shape (num_time_series, num_obs_to_train + seq_len)
sigma (array like): shape (num_time_series, num_obs_to_train + seq_len)
'''
if isinstance(X, type(np.empty(2))): # 转换为tensor
X = torch.from_numpy(X).float()
y = torch.from_numpy(y).float()
Xf = torch.from_numpy(Xf).float()
num_ts, num_obs_to_train, _ = X.size()
_, seq_len, num_features = Xf.size()
ynext = None
ypred = []
mus = []
sigmas = []
h, c = None, None
# 遍历所有时间点
for s in range(num_obs_to_train + seq_len): # num_obs_to_train为历史序列长度,seq_len为预测长度
if s < num_obs_to_train: # Encoder,ynext为真实值
if s == 0: ynext = torch.zeros((num_ts,1)).to(device)
else: ynext = y[:, s-1].view(-1, 1) # (num_ts,1) # 取上一时刻的真实值
yembed = self.input_embed(ynext).view(num_ts, -1) # (num_ts,embedding_size)
x = X[:, s, :].view(num_ts, -1) # (num_ts,num_features)
else: # Decoder,ynext为预测值
if s == num_obs_to_train: ynext = y[:, s-1].view(-1, 1) # (num_ts,1) # 预测的第一个时间点取上一时刻的真实值
yembed = self.input_embed(ynext).view(num_ts, -1) # (num_ts,embedding_size)
x = Xf[:, s-num_obs_to_train, :].view(num_ts, -1) # (num_ts,num_features)
x = torch.cat([x, yembed], dim=1) # (num_ts, num_features + embedding)
inp = x.unsqueeze(1) # (num_ts,1, num_features + embedding)
if h is None and c is None:
out, (h, c) = self.encoder(inp) # h size (num_layers, num_ts, hidden_size)
else:
out, (h, c) = self.encoder(inp, (h, c))
hs = h[-1, :, :] # (num_ts, hidden_size)
hs = F.relu(hs) # (num_ts, hidden_size)
mu, sigma = self.likelihood_layer(hs) # (num_ts, 1)
mus.append(mu.view(-1, 1))
sigmas.append(sigma.view(-1, 1))
if self.likelihood == "g":
ynext = gaussian_sample(mu, sigma) #(num_ts, 1)
elif self.likelihood == "nb":
alpha_t = sigma
mu_t = mu
ynext = negative_binomial_sample(mu_t, alpha_t) #(num_ts, 1)
# if without true value, use prediction
if s >= num_obs_to_train and s < num_obs_to_train + seq_len: #在预测区间内
ypred.append(ynext)
ypred = torch.cat(ypred, dim=1).view(num_ts, -1) #(num_ts, seq_len)
mu = torch.cat(mus, dim=1).view(num_ts, -1) #(num_ts, num_obs_to_train + seq_len)
sigma = torch.cat(sigmas, dim=1).view(num_ts, -1) #(num_ts, num_obs_to_train + seq_len)
return ypred, mu, sigma
Load Data
num_epoches = 100
step_per_epoch = 3 #在一个epoch中,从训练集中提取step_per_epoch次训练数据
lr = 1e-3
n_layers = 1
hidden_size = 50
embedding_size = 10 #将上一时刻的真实值编码为embedding_size长度
likelihood = "g"
seq_len = 60 #预测的未来窗口长度
num_obs_to_train = 168 #训练的历史窗口长度
num_results_to_sample = 10
show_plot = True
run_test = True
standard_scaler = True
log_scaler = False
mean_scaler = False
batch_size = 64
sample_size = 100
device=torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# 读取数据
data = pd.read_csv("LD_MT200_hour.csv", parse_dates=["date"])
data["year"] = data["date"].apply(lambda x: x.year)
data["day_of_week"] = data["date"].apply(lambda x: x.dayofweek)
data = data.loc[(data["date"].dt.date >= date(2014, 1, 1)) & (data["date"].dt.date <= date(2014, 3, 1))]
print(data.shape)
plt.figure(figsize=(16, 4))
plt.plot(data['MT_200'])
data.head()
![]()
# 数据预处理
features = ["hour", "day_of_week"]
# hours = pd.get_dummies(data["hour"])
# dows = pd.get_dummies(data["day_of_week"])
years = data["year"]
hours = data["hour"]
dows = data["day_of_week"]
# MT_200 = data["MT_200"]
# yscaler = StandardScaler()
# MT_200 = yscaler.fit_transform(MT_200)
X = np.c_[np.asarray(hours),np.asarray(dows)] #X:(len,features)
num_features = X.shape[1]
num_periods = len(data)
X = np.asarray(X).reshape((-1, num_periods, num_features))
y = np.asarray(data["MT_200"]).reshape((-1, num_periods))
print("X_shape=",X.shape) # (series_num,len,features_num)
print("y_shape=",y.shape) # (series_num,len)
# X = np.tile(X, (10, 1, 1))
# y = np.tile(y, (10, 1))
输出:
X_shape= (1, 1440, 2)
y_shape= (1, 1440)
# 滑动窗口
def sliding_window(DataSet, width, multi_vector = True): #DataSet has to be as an Array
if multi_vector: #三维 (num_samples,length,features)
num_samples,length,features = DataSet.shape
else: #二维 (num_samples,length)
DataSet = DataSet[:,:,np.newaxis] #(num_samples,length,1)
num_samples,length,features = DataSet.shape
x = DataSet[:,0:width,:] #(num_samples,width,features)
x = x[np.newaxis,:,:,:] #(1,num_samples,width,features)
for i in range(length - width):
i += 1
tmp = DataSet[:,i:i + width,:]#(num_samples,width,features)
tmp = tmp[np.newaxis,:,:,:] #(1,num_samples,width,features)
x = np.concatenate([x,tmp],0) #(i+1,num_samples,width,features)
return x
width = num_obs_to_train + seq_len
X_data = sliding_window(X, width, multi_vector = True) #(len-width+1,num_samples,width,features)
Y_data = sliding_window(y, width, multi_vector = False) #(len-width+1,num_samples,width,1)
print("x的维度为:",X_data.shape)
print("y的维度为:",Y_data.shape)
# 取其中一类序列
i = 0
X_data = X_data[:,i,:,:]
Y_data = Y_data[:,i,:,0]
print("x的维度为:",X_data.shape)
print("y的维度为:",Y_data.shape)
输出:
x的维度为: (1213, 1, 228, 2)
y的维度为: (1213, 1, 228, 1)
x的维度为: (1213, 228, 2)
y的维度为: (1213, 228)
# SPLIT TRAIN TEST
from sklearn.model_selection import train_test_split
Xtr, Xte, ytr, yte = train_test_split(X_data, Y_data,
test_size=0.3,
random_state=0,
shuffle=False)
print("X_train:{},y_train:{}".format(Xtr.shape,ytr.shape))
print("X_test:{},y_test:{}".format(Xte.shape,yte.shape))
输出:
X_train:(849, 228, 2),y_train:(849, 228)
X_test:(364, 228, 2),y_test:(364, 228)
# 标准化
yscaler = None
if standard_scaler:
yscaler = StandardScaler()
elif log_scaler:
yscaler = LogScaler()
elif mean_scaler:
yscaler = MeanScaler()
if yscaler is not None:
ytr = yscaler.fit_transform(ytr)
#构造Dtaloader
Xtr=torch.as_tensor(torch.from_numpy(Xtr), dtype=torch.float32)
ytr=torch.as_tensor(torch.from_numpy(ytr),dtype=torch.float32)
Xte=torch.as_tensor(torch.from_numpy(Xte), dtype=torch.float32)
yte=torch.as_tensor(torch.from_numpy(yte),dtype=torch.float32)
train_dataset=torch.utils.data.TensorDataset(Xtr,ytr) #训练集dataset
train_Loader=torch.utils.data.DataLoader(train_dataset,batch_size=batch_size)
Train
Args:
- X (array like): shape (num_samples, num_periods, num_features)
- y (array like): shape (num_samples, num_periods)
- epochs (int): number of epochs to run
- step_per_epoch (int): steps per epoch to run
- num_obs_to_train (int): The length of the history window for training
- seq_len (int): output horizon
- likelihood (str): what type of likelihood to use, default is gaussian
- num_skus_to_show (int): how many skus to show in test phase
- num_results_to_sample (int): how many samples in test phase as prediction
# 定义模型和优化器
num_ts, num_periods, num_features = X.shape
model = DeepAR(num_features, embedding_size,
hidden_size, n_layers, lr, likelihood).to(device)
optimizer = Adam(model.parameters(), lr=lr)
random.seed(2)
losses = []
cnt = 0
# training
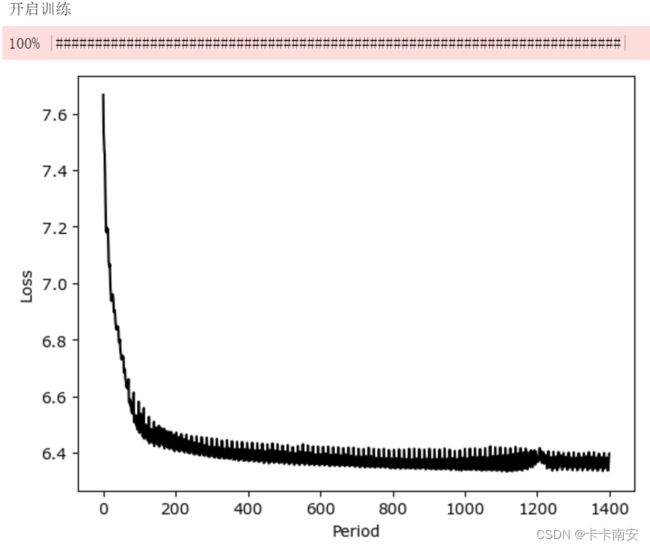
print("开启训练")
progress = ProgressBar()
for epoch in progress(range(num_epoches)):
# print("Epoch {} starts...".format(epoch))
for x,y in train_Loader:
x = x.to(device) # (batch_size, num_obs_to_train+seq_len, num_features)
y = y.to(device) # (batch_size, num_obs_to_train+seq_len)
Xtrain = x[:,:num_obs_to_train,:].float() # (batch_size, num_obs_to_train, num_features)
ytrain = y[:,:num_obs_to_train].float() # (batch_size, num_obs_to_train)
Xf = x[:,-seq_len:,:].float() # (batch_size, seq_len, num_features)
yf = y[:,-seq_len:].float() # (batch_size, seq_len)
ypred, mu, sigma = model(Xtrain, ytrain, Xf) # ypred:(batch_size, seq_len), mu&sigma:(batch_size, num_obs_to_train + seq_len)
# ypred_rho = ypred
# e = ypred_rho - yf
# loss = torch.max(rho * e, (rho - 1) * e).mean()
## gaussian loss
ytrain = torch.cat([ytrain, yf], dim=1) # (batch_size, num_obs_to_train+seq_len)
if likelihood == "g":
loss = gaussian_likelihood_loss(ytrain, mu, sigma)
elif likelihood == "nb":
loss = negative_binomial_loss(ytrain, mu, sigma)
losses.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
cnt += 1
# 绘制loss
if show_plot:
plt.plot(range(len(losses)), losses, "k-")
plt.xlabel("Period")
plt.ylabel("Loss")
plt.show()
Test
# test
print("开启测试")
X_test_sample = Xte[:,:,:].reshape(-1,num_obs_to_train+seq_len,num_features).to(device) # (num_samples, num_obs_to_train+seq_len, num_features)
y_test_sample = yte[:,:].reshape(-1,num_obs_to_train+seq_len).to(device) # (num_samples, num_obs_to_train+seq_len)
X_test = X_test_sample[:,:num_obs_to_train,:] # (num_samples, num_obs_to_train, num_features)
Xf_test = X_test_sample[:, -seq_len:, :] # (num_samples, seq_len, num_features)
y_test = y_test_sample[:, :num_obs_to_train] # (num_samples, num_obs_to_train)
yf_test = y_test_sample[:, -seq_len:] # (num_samples, seq_len)
if yscaler is not None:
y_test = yscaler.transform(y_test)
result = []
n_samples = sample_size # 采样个数
for _ in tqdm(range(n_samples)):
y_pred, _, _ = model(X_test, y_test, Xf_test) # ypred:(num_samples, seq_len)
y_pred = y_pred.cpu().numpy()
if yscaler is not None:
y_pred = yscaler.inverse_transform(y_pred)
result.append(y_pred[:,:,np.newaxis]) # y_pred[:,:,np.newaxis]:(num_samples, seq_len,1)
# result.append(y_pred.reshape((-1, 1)))
result = np.concatenate(result, axis=2) # (num_samples, seq_len, n_samples)
p50 = np.quantile(result, 0.5, axis=2) # (num_samples, seq_len)
p90 = np.quantile(result, 0.9, axis=2) # (num_samples, seq_len)
p10 = np.quantile(result, 0.1, axis=2) # (num_samples, seq_len)
i = -1 #选取其中一条序列进行可视化
if show_plot: # 序列总长度为:历史窗口长度(num_obs_to_train)+预测长度(seq_len)
plt.figure(1, figsize=(20, 5))
plt.plot([k + seq_len + num_obs_to_train - seq_len for k in range(seq_len)], p50[i,:], "r-") # 绘制50%分位数曲线
# 绘制10%-90%分位数阴影
plt.fill_between(x=[k + seq_len + num_obs_to_train - seq_len for k in range(seq_len)], y1=p10[i,:], y2=p90[i,:], alpha=0.5)
plt.title('Prediction uncertainty')
yplot = y_test_sample[i,:].cpu() #真实值 (1, seq_len+num_obs_to_train)
plt.plot(range(len(yplot)), yplot, "k-")
plt.legend(["P50 forecast", "P10-P90 quantile", "true"], loc="upper left")
ymin, ymax = plt.ylim()
plt.vlines(seq_len + num_obs_to_train - seq_len, ymin, ymax, color="blue", linestyles="dashed", linewidth=2)
plt.ylim(ymin, ymax)
plt.xlabel("Periods")
plt.ylabel("Y")
plt.show()
#评价指标
pred_up = p90[:,:].reshape(-1,seq_len) #(num_samples,seq_len)
pred_mid = p50[:,:].reshape(-1,seq_len) #(num_samples,seq_len)
pred_low = p10[:,:].reshape(-1,seq_len) #(num_samples,seq_len)
true = yf_test.cpu().detach().numpy()[:,:].reshape(-1,seq_len) #(num_samples,seq_len)
test_samples, seq_len = true.shape
u = 0.9-0.1
# 1. PICP(PI coverage probability) 要求大于等于区间分位数
PICP = 0
for i in range(test_samples):
count = 0
for j in range(seq_len):
if true[i,j] > pred_low[i,j] and true[i,j] < pred_up[i,j]:
count += 1
picp = count / seq_len
PICP += picp
PICP = PICP / test_samples
print("PICP:",PICP)
# 2. PINAW(PI normalized averaged width) 用于定义区间的狭窄程度,在保证准确性的前提下越小越好
PINAW = 0
for i in range(test_samples):
width = 0
true_max = np.max(true[i,:])
true_min = np.min(true[i,:])
for j in range(seq_len):
width += (pred_up[i,j]-pred_low[i,j])
width /= seq_len
pinaw = (width / (true_max-true_min))
PINAW += pinaw
PINAW = PINAW / test_samples
print("PINAW:",PINAW)
# 3. CWC(coverage width-based criterion) 综合考虑区间覆盖率和狭窄程度, 越小越好
g = 90 #取值在50-100
error = math.exp(-g * (PICP - u))
if PICP >= u:
r = 0
else:
r = 1
CWC = PINAW * (1 + r * error)
print("CWC:",CWC)
# 4. CRPS(continuous ranked probability score) 综合评价指标,量化一个连续概率分布(理论值)与确定性观测样本(真实值)间的差异,可视为平均绝对误差(MAE)在连续概率分布上的推广
# https://avoid.overfit.cn/post/302f7305a414449a9eb2cfa628d15853
def crps(y_true, y_pred, sample_weight=None):
num_samples = y_pred.shape[0]
absolute_error = np.mean(np.abs(y_pred - y_true), axis=0)
if num_samples == 1:
return np.average(absolute_error, weights=sample_weight)
y_pred = np.sort(y_pred, axis=0) #(3,60)
diff = y_pred[1:] - y_pred[:-1] #一阶差分
weight = np.arange(1, num_samples) * np.arange(num_samples - 1, 0, -1)
weight = np.expand_dims(weight, -1)
per_obs_crps = absolute_error - np.sum(diff * weight, axis=0) / num_samples**2
return np.average(per_obs_crps, weights=sample_weight)
CRPS = 0
for i in range(test_samples):
y_pred = np.concatenate([pred_up[i,None,:],pred_mid[i,None,:],pred_low[i,None,:]],axis=0) #(3,60)
y_true = true[i,:] #(1,60)
c = crps(y_true,y_pred)
CRPS += c
CRPS = CRPS / test_samples
print("CRPS:",CRPS)
# 5. P50 quantile MAE
MAE = 0
for i in range(test_samples):
error = 0
for j in range(seq_len):
error += np.abs(true[i,j]-pred_mid[i,j])
mae = error / seq_len
MAE += mae
MAE = MAE / test_samples
print("P50 quantile MAE:",MAE)
# 6. # P50 quantile MAPE
MAPe = 0
for i in range(test_samples):
mape = MAPE(true[i,:], pred_mid[i,:])
MAPe += mape
MAPe = MAPe / test_samples
print("P50 quantile MAPE: {}".format(MAPe))
输出:
PICP: 0.9852106227106228
PINAW: 0.23486948616378414
CWC: 0.23486948616378414
CRPS: 96.34482641472391
P50 quantile MAE: 86.1149369879084
P50 quantile MAPE: 0.034020405319259976