【算法】道路与航线（保姆级题解）

题目

农夫约翰正在一个新的销售区域对他的牛奶销售方案进行调查。

他想把牛奶送到 T 个城镇，编号为 1∼T。

（存在T个点）

这些城镇之间通过 R 条道路 (编号为 1 到 R) 和 P 条航线 (编号为 1 到 P) 连接。

（存在R条道路，P条航线）

每条道路 i 或者航线 i 连接城镇 Ai 到 Bi，花费为 Ci。

对于道路，0 ≤ Ci ≤ 10,000; 然而航线的花费很神奇，花费 Ci 可能是负数(−10,000 ≤ Ci ≤10,000)。

 （道路权值为正，航线的权值可能为负）

道路是双向的，可以从 Ai 到 Bi，也可以从 Bi 到 Ai，花费都是 Ci。

 （道路是双向的）

然而航线与之不同，只可以从 Ai 到 Bi。

事实上，由于最近恐怖主义太嚣张，为了社会和谐，出台了一些政策：保证如果有一条航线可以从 Ai 到 Bi，那么保证不可能通过一些道路和航线从 Bi 回到 Ai。

（航线是单向的，并且保证岛屿所构成的图没有回路） 

由于约翰的奶牛世界公认十分给力，他需要运送奶牛到每一个城镇。

他想找到从发送中心城镇 S 把奶牛送到每个城镇的最便宜的方案。

输入格式

第一行包含四个整数 T,R,P,S。

接下来 R 行，每行包含三个整数（表示一个道路）Ai,Bi,Ci。

接下来 P 行，每行包含三个整数（表示一条航线）Ai,Bi,Ci。

输出格式

第 1..T 行：第 i 行输出从 S 到达城镇 i 的最小花费，如果不存在，则输出 NO PATH。

数据范围

1 ≤ T ≤ 25000
1 ≤ R , P ≤ 50000
1 ≤ Ai , Bi , S ≤ T

思路

 由题意，我们可知：

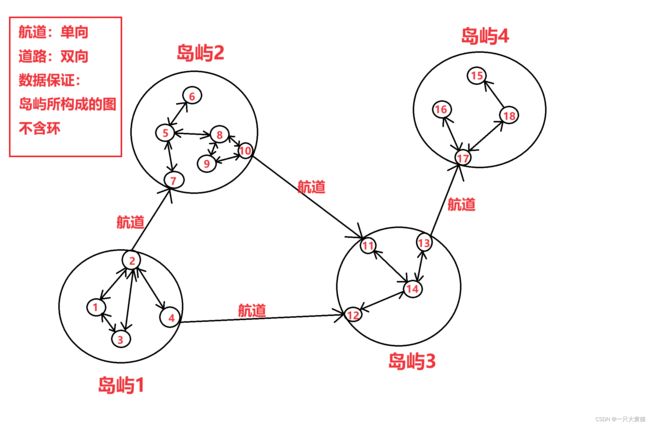
小镇在岛屿上，一个小镇可能通过航道连接其他岛屿的小镇，岛屿构成的边是有向无环图。

岛屿上的小镇通过无向边连接，由此，我们可以构造出下面这张图。

1、将城镇道路输入，使用邻接表储存（无向图）

while(mr --)// 输入道路数 
    {
        int a,b,c;
        cin >> a >> b >> c;
        add(a,b,c),add(b,a,c);// 建立无向图 
    }

void add(int a,int b,int c)// 建立邻接表 
{
    e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx ++;
} 

 2、我们先将每个城镇与他所在的岛屿编号绑定起来（一个岛屿可以有多个城镇，一个城镇只能属于一个岛屿）。

for(int i = 1; i <= n; i ++)
        if(!id[i])
            dfs(i,++ bcnt);

// 循环结束后，block[i][j]表示点j在岛屿i上，id[i]等于点i的岛屿编号 

void dfs(int u,int bid)// 深度搜索 
{
    id[u] = bid;// 点u在岛屿bid上 （类似于并查集的祖宗节点） 
    block[bid].push_back(u);// 将点u储存到bid岛屿上 
    for(int i = h[u]; ~i ; i = ne[i])// 与点u通过道路连接的点，均在同一岛屿上 
    {
        int j = e[i];
        if(!id[j]) dfs(j,bid);// 进行深搜，如果点j还没有存入岛屿，进行遍历 
    }
}
3、输入航道，建立有向无环图（并记录岛屿的入度为topsort做准备）
    while(mp --)// 输入航道数 
    {
        int a,b,c;
        cin >> a >> b >> c;
        add(a,b,c);// 建立有向图 
        din[id[b]] ++;// b点的入度+1 
    }

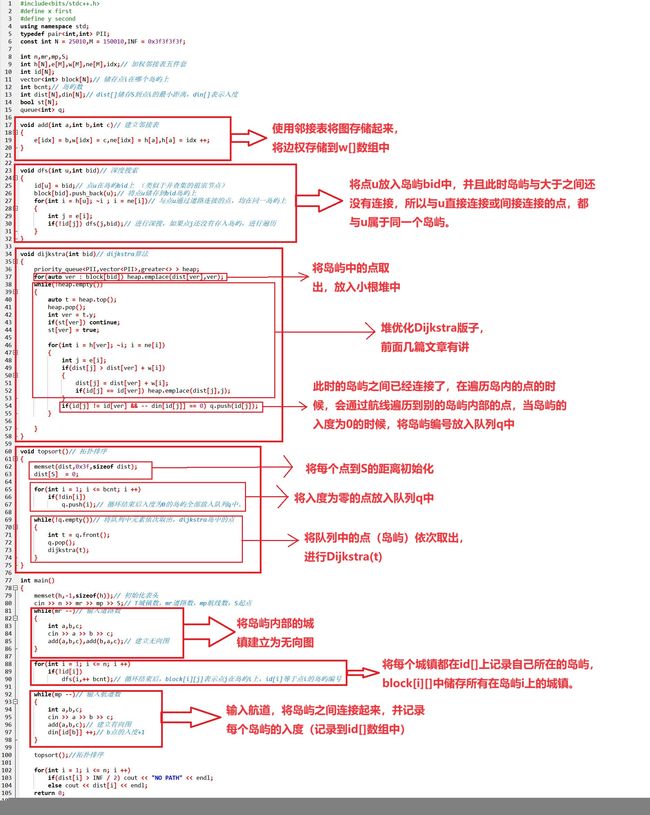
4、进行拓扑排序，将入度为零的点放入数组中，依次遍历入度为0的点。

略（在代码详解部分有详细解释） 

代码 

#include
#define x first
#define y second
using namespace std;
typedef pair PII;
const int N = 25010,M = 150010,INF = 0x3f3f3f3f;

int n,mr,mp,S;
int h[N],e[M],w[M],ne[M],idx;// 加权邻接表五件套 
int id[N];
vector block[N];// 储存点i在哪个岛屿上 
int bcnt;// 岛屿数 
int dist[N],din[N];// dist[]储存S到点i的最小距离，din[]表示入度 
bool st[N];
queue q;

void add(int a,int b,int c)// 建立邻接表 
{
	e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx ++;
}


void dfs(int u,int bid)// 深度搜索 
{
	id[u] = bid;// 点u在岛屿bid上 （类似于并查集的祖宗节点） 
	block[bid].push_back(u);// 将点u储存到bid岛屿上 
	for(int i = h[u]; ~i ; i = ne[i])// 与点u通过道路连接的点，均在同一岛屿上 
	{
		int j = e[i];
		if(!id[j]) dfs(j,bid);// 进行深搜，如果点j还没有存入岛屿，进行遍历 
	}
}

void dijkstra(int bid)// dijkstra算法 
{
	priority_queue,greater<> > heap;
	for(auto ver : block[bid]) heap.emplace(dist[ver],ver);
	while(!heap.empty())
	{
		auto t = heap.top();
		heap.pop();
		int ver = t.y;
		if(st[ver]) continue;
        st[ver] = true;

		for(int i = h[ver]; ~i; i = ne[i])
		{
			int j = e[i];
			if(dist[j] > dist[ver] + w[i])
			{
				dist[j] = dist[ver] + w[i];
				if(id[j] == id[ver]) heap.emplace(dist[j],j);
			}
			if(id[j] != id[ver] && -- din[id[j]] == 0) q.push(id[j]);
		}

	}
}

void topsort()// 拓扑排序 
{
	memset(dist,0x3f,sizeof dist);
	dist[S]  = 0;

	for(int i = 1; i <= bcnt; i ++)
		if(!din[i])
			q.push(i);// 循环结束后入度为0的岛屿全部放入队列q中。 
	
	while(!q.empty())// 将队列中元素依次取出，dijkstra岛中的点 
	{
		int t = q.front();
		q.pop();
		dijkstra(t);
	}
}

int main()
{
	memset(h,-1,sizeof(h));// 初始化表头 
	cin >> n >> mr >> mp >> S;// T城镇数，mr道路数，mp航线数，S起点 
	while(mr --)// 输入道路数 
	{
		int a,b,c;
		cin >> a >> b >> c;
		add(a,b,c),add(b,a,c);// 建立无向图 
	}
	
	for(int i = 1; i <= n; i ++)
		if(!id[i])
			dfs(i,++ bcnt);// 循环结束后，block[i][j]表示点j在岛屿i上，id[i]等于点i的岛屿编号 
	
	while(mp --)// 输入航道数 
	{
		int a,b,c;
		cin >> a >> b >> c;
		add(a,b,c);// 建立有向图 
		din[id[b]] ++;// b点的入度+1 
	}
	
	topsort();//拓扑排序 

	for(int i = 1; i <= n; i ++)
		if(dist[i] > INF / 2) cout << "NO PATH" << endl;
		else cout << dist[i] << endl;
	return 0;
}

代码详解