Deep Reinforcement Learning --- Value Based Methods --- Chapter 2-2 Deep Q-Networks

Deep Reinforcement Learning — Value Based Methods — Chapter 2-2 Deep Q-Networks

2.2.1 From RL to Deep RL

  So far, you’ve solved many of your own reinforcement learning problems, using solution methods that represent the action values in a small table. Earlier in the nanodegree, we referred to this table as a Q-table.

  You have already worked with some Deep Learning Neural Networks for classification, detection and segmentation. However, these Deep Learning Applications use label training data for supervised learning. The inference engine then produces the best guess label, not an action, as the output. When an oral agent handles the entire end-to-end pipeline, it’s called pixels-to-action, referring to the networks ability to take raw sensor data and choose the action, it thinks will best maximize its reward. Over time, oral agents have a uncanny knack for developing intuitive human-like learning to walk or peeking behind corners when they’re unsrue.

  They naturally incorporate elements of exploration and knowledge gathering, which makes them good for imitating behaviors and performing path planning. Robots operating in unstructured environments tend to greatly benefit from oral agents.

 As you’ll learn in this lesson, the Deep Q-Learning algorithm represents the optimal action-value function $q_{\ast }$ as a neural network (instead of a table).

  Unfortunately, reinforcement learning is notoriously unstable when neural networks are used to represent the action values. In this lesson, you’ll learn all about the Deep Q-Learning algorithm, which addressed these instabilities by using two key features:

• Experience Replay
• Fixed Q-Targets

  There are few very useful additions and tweaks though, in DQN. The first edition is the use of a rolly history of the past data via replay pool. By using the replay pool, the behavior distribution is average over many of its previous states, smoothing out learning and avoiding oscillations. This has the advantage that, each step of the experience is potentially used in many weight updates.
  The other big idea is the use of a target network to represent the Q-function, which will be used to compute the loss of every action during training. Why not use a single network? Well, the issue is that at each step of training, the Q-fucntions values change and then the value estimates can easily spiral out of control. These additions enable RL agents to converge, more reliably during training.

2.2.2 Deep Q-Networks

• In order to capture temporal information, a stack of 4 preprocessing frames are used as the state that is passed to the DQN.
• The DQN takes the states as inputs, and returns the corresponding predicted action values for each possible game action.
• The DQN architecture is composed of a couple of convolutional layers, followd by a couple of fully connected layers.

2.2.3 Experience Replay

  By using the experienve replay methods, we can turn the reinforcement learning into supervised learning.

  When the agent interacts with the environment, the sequence of experience tuples can be highly correlated. The naive Q-learning algorithm that learns from each of these experience tuples in sequential order runs the risk of getting swayed by the effects of this correlation. By instead keeping track of a replay buffer and using experience replay to sample from the buffer at random, we can prevent action values from oscillaing of diverging catastrophically.

  The replay buffer contains a collection of experience tuples $\left(S,A,R,S^{\prime }\right)$, The tuples are gradually added to the buffer as we are interacting with the environment.

  The act of sampling a small batch of tuples from the replay buffer in order to learn is known as experience replay. In order to breaking harmful correlations, experience replay allows us to learn more from individual tuples, recall rare occurrences, and in general make better use of our experience.

• Experience replay is based on the idea that we can learn better, if we do multiple passes over the same experience.
• Experience replay is used to generate uncorrelated experience data for online training of deep RL agents.

2.2.4 Fixed Q-Targets

  Experience replay helps us address one type of correlation. That is between consecutive experience tuples.

  There is another kind of correlation that Q-Learning is susceptible to. Q-learning is a form of Temporal Difference of TD learning.

  Our goal is to reduce the difference between the TD Target and the currently predicted Q-Value (TD Predict), this difference is the TD error. Now, the TD target here is supposed to be a replacement for the true value function $q_{\pi }\left(s,a\right)$ which is unknown to us.

  We originally used $q_{\pi }$ to define a squared error loss:
$$J\left(\omega \right)={\mathbb{E}}_{\pi }\left[{\left(q_{\pi }\left(S,A\right)-\hat{q}\left(S,A,\omega \right)\right)}^2\right]$$
  And differentiated that with respect to $\omega$ to get the gradient descent update rule. (获取梯度的方向)
$${\nabla }_{\omega }J\left(\omega \right)=-2\left(q_{\pi }\left(S,A\right)-\hat{q}\left(S,A,\omega \right)\right){\nabla }_{\omega }\hat{q}\left(S,A,\omega \right)$$

根据梯度的方向，在其反方向，进行权重的更新
$$\begin{gathered} \Delta \omega =-\alpha \frac{1}{2}{\nabla }_{\omega }J\left(\omega \right) \\ =\alpha \left(q_{\pi }\left(S,A\right)-\hat{q}\left(S,A,\omega \right)\right){\nabla }_{\omega }\hat{q}\left(S,A,\omega \right) \end{gathered}$$
即：
$$\Delta \omega =\alpha \cdot \stackrel{\text{TD error}}{\underset{\text{TD Target}}{R+\gamma \underset{a}{\max }\hat{q}\left(S^{\prime },a,{\omega }^{-}\right)}-\underset{\text{TD Predict}}{\hat{q}\left(S,A,\omega \right)}}{\nabla }_{\omega }\hat{q}\left(S,A,\omega \right)$$
where $w^{-}$ are the weights of a separate target network that are not changed during the learning step, and $(S,A,R,S^{\prime })$ is an experience tuple.
  In practice, we use $w^{-}$ to generate targets while changing w for a certain number of learning steps. Then, we update $w^{-}$ with the latest w. This decouples the target from the parameters, makes the learning algorithm much more stable and less likely to diverge or fall into oscillations.

Here, $q_{\pi }\left(S,A\right)$ is not dependent on our function approximation or its parameters, but the TD Target is dependent on these parameters which means simply replacing the true value function $q_{\pi }$ with a target is mathematically incorrect. We can get away with it in practice because every update results in a small change to the parameters. We’re just generally in the right direction.

• The Deep Q-Learning algorithms used two separate networks with identical architectures.
• The target Q-Network’s weights are updated less often (or more slowly) than the primary Q-Network.
• Without fixed Q-targets, we would encounter a harmful form of correlation, whereby we shift the parameters of the network based on a constantly moving target.

2.2.5 Deep Q-Networks

  There are two main processes that are interleaved in this algorithm. One, is where we sample the envirnment by performing actions and store away the observed experienced tuples in a replay memeory.

  The other is where we select the small batch of tuples from this memory randomly, and learn from that batch using a gradient descent update step.

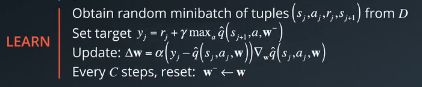
These two processes are not directly dependent on each other. So, you could perform multiple sampling steps then one learning step, or even multiple learning steps with different random batches.

There are many other techniques and optimizations that are used in the DQN paper, such as reward clippling, error clipping, storing past actions as part of the state vector, dealing with terminal states, digging epsilon over time, etc.

2.2.6&7 Coding Exercise & Workspace

• 初始状态
• 智能体选取动作
• 基于状态与选定的动作，与环境进行交互
• 环境返回下一个状态、奖励、是否停止
• 将该条信息存入经验池，并从经验池中采样一个batch样本
• 模型训练
  • 拆解样本条目为states，actions，rewards，next_states，dones
  • 由目标网络和next_states获取当前网络参数下的动作值函数 Q_target_next
  • 由$rewards+\gamma Q\_targets\_next$获取$Q\_targets$
  • 由预测网络获取期望动作值函数
  • 组合求解loss
  • 模型反向传播，优化参数
  • 更新目标网络与预测网络参数
• 进入下一个状态，将累计奖励记下来。

# Deep Q-Network (DQN)
---
In this notebook, you will implement a DQN agent with OpenAI Gym's LunarLander-v2 environment.

### 1. Import the Necessary Packages

import gym
!pip3 install box2d
import random
import torch
import numpy as np
from collections import deque
import matplotlib.pyplot as plt
%matplotlib inline

!python -m pip install pyvirtualdisplay
from pyvirtualdisplay import Display
display = Display(visible=0, size=(1400, 900))
display.start()

is_ipython = 'inline' in plt.get_backend()
if is_ipython:
    from IPython import display

plt.ion()

### 2. Instantiate the Environment and Agent

Initialize the environment in the code cell below.

env = gym.make('LunarLander-v2')
env.seed(0)

print('State shape: ', env.observation_space.shape)
print('Number of actions: ', env.action_space.n)

from dqn_agent import Agent
agent = Agent(state_size=8, action_size=4, seed=0)

# watch an untrained agent 
state = env.reset()
img = plt.imshow(env.render(mode='rgb_array'))
for j in range(200):
    action = agent.act(state)
    img.set_data(env.render(mode='rgb_array'))
    plt.axis('off')
    display.display(plt.gcf())
    display.clear_output(wait=True)
    state, rewared, done, _ = env.step(action)
    if done:
        break
env.close()

**### 3. Train the Agent with DQN

Run the code cell below to train the agent from scratch.  You are welcome to amend the supplied values of the parameters in the function, to try to see if you can get better performance!
Alternatively, you can skip to the next step below (**4. Watch a Smart Agent!**), to load the saved model weights from a pre-trained agent.**

def dqn(n_episodes=2000, max_t=1000, eps_start=1.0, eps_end=0.01, eps_decay=0.995):
    """Deep Q-Learning.
    
    Params
    ======
        n_episodes (int): maximum number of training episodes
        max_t (int): maximum number of timesteps per episode
        eps_start (float): starting value of epsilon, for epsilon-greedy action selection
        eps_end (float): minimum value of epsilon
        eps_decay (float): multiplicative factor (per episode) for decreasing epsilon
    """
    scores = [] # list containing socres from each episode
    scores_window = deque(maxlen=100) # last 100 scores
    eps = eps_start
    for i_episode in range(1, n_episodes+1):
        state = env.reset()
        score = 0
        for t in range(max_t):
            action = agent.act(state, eps)
            next_state, reward, done, _ = env.step(action)
            agent.step(state, action, reward, next_state, done)
            state = next_state
            score += reward
            if done:
                break
        scores_window.append(score) # save most recent score
        scores.append(score) # save most recent score
        eps = max(eps_end, eps_decay * eps) # decreate epsilon
        print('\rEpisode {} \tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_window)), end='')

        if i_episode % 100 == 0:
            print('\rEpisode {} \tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_window)))

        if np.mean(scores_window) >= 200:
            print('\nEnvironment solved in {:d} episodes! \t Average Score: {:.2f}'.format(i_episode-100, np.mean(scores_window)))
            torch.save(agent.q_network_local.state_dict(), 'checkpoint.pth')
            break
    return scores

scores = dqn()

# plot the scores 
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores)
plt.ylabel("Score")
plt.xlabel("Episode # ")
plt.show()

### 4. Watch a Smart Agent!
In the next code cell, you will load the trained weights from file to watch a smart agent!

# load the weights from file 
agent.q_network_local.load_state_dict(torch.load('checkpoint.pth'))

for i in range(3):
    state = env.reset()
    img = plt.imshow(env.render(mode='rgb_array'))
    for j in range(200):
        action = agent.act(state)
        img.set_data(env.render(mode='rgb_array'))
        plt.axis('off')
        display.display(plt.gcf())
        display.clear_output(wait=True)
        state, reward, done, _ = env.step(action)
        if done:
            break
env.close(0)

### 5. Explore

In this exercise, you have implemented a DQN agent and demonstrated how to use it to solve an OpenAI Gym environment.  To continue your learning, you are encouraged to complete any (or all!) of the following tasks:
- Amend the various hyperparameters and network architecture to see if you can get your agent to solve the environment faster.  Once you build intuition for the hyperparameters that work well with this environment, try solving a different OpenAI Gym task with discrete actions!
- You may like to implement some improvements such as prioritized experience replay, Double DQN, or Dueling DQN! 
- Write a blog post explaining the intuition behind the DQN algorithm and demonstrating how to use it to solve an RL environment of your choosing.  

model.py 文件中的内容

import torch
import torch.nn as nn
import torch.nn.functional as F

class QNetwork(nn.Module):
    """Actor (Policy) Model."""
    def __init__(self, state_size, action_size, seed, fc1_units=64, fc2_units=64):
        """Initialize parameters and build model.
        Params
        ======
            state_size (int): Dimension of each state
            action_size (int): Dimension of each action
            seed (int): Random seed
            fc1_units (int): Number of nodes in first hidden layer
            fc2_units (int): Number of nodes in second hidden layer
        """
        super(QNetwork, self).__init__()
        self.seed = torch.manual_seed(seed)
        self.fc1 = nn.Linear(state_size, fc1_units)
        self.fc2 = nn.Linear(fc1_units, fc2_units)
        self.fc3 = nn.Linear(fc2_units, action_size)
        
    def forward(self, state):
        """Build a network that maps state -> action values."""
        x = F.relu(self.fc1(state))
        x = F.relu(self.fc2(x))
        return self.fc3(x)
    

dqn_agent.py 中的内容：

#! /usr/bin/env python3
# coding=utf-8
import numpy as np
import random
from collections import namedtuple, deque

from model import QNetwork

import torch
import torch.nn.functional as F
import torch.optim as optim

BUFFER_SIZE = int(1e5)  # replay buffer size
BATCH_SIZE = 64  # minibatch size
GAMMA = 0.99  # discount factor
TAU = 1e-3  # for soft update of
LEARNING_RATE = 5e-4  # learning rate
UPDATE_EVERY = 4  # how often to update the network

device = torch.device("cuda:2" if torch.cuda.is_available() else "cpu")

print(device)

class Agent():
    """Interacts with and learns from the environment."""

    def __init__(self, state_size, action_size, seed):
        """Initialize an Agent object.

        Params
        ======
            state_size (int): dimension of each state
            action_size (int): dimension of each action
            seed (int): random seed
        """
        self.state_size = state_size
        self.action_size = action_size
        self.seed = random.seed(seed)
        
        # Q-Network
        self.q_network_local = QNetwork(state_size, action_size, seed).to(device)
        self.q_network_target = QNetwork(state_size, action_size, seed).to(device)
        self.optimizer = optim.Adam(self.q_network_local.parameters(), lr=LEARNING_RATE)    
        
        # Replay memory
        self.memory = ReplayBuffer(action_size, BUFFER_SIZE, BATCH_SIZE, seed)    
        # Initialize time step (for updating every UPDATE_EVERY steps)
        self.t_step = 0 
    
    def step(self, state, action, reward, next_state, done):
        # Save experiences in replay memory
        self.memory.add(state, action, reward, next_state, done)
        
        # Learn every UPDATE_EVERY time stpes.
        self.t_step = (self.t_step + 1) % UPDATE_EVERY
        if self.t_step == 0:
            # If enough samples are available in memory, get random subset and learn
            if len(self.memory) > BATCH_SIZE:
                experiences = self.memory.sample()
                self.learn(experiences, GAMMA)
                
    def act(self, state, eps=0):
        """Returns actions for given state as per current policy
        
        Params
        ======
            state (array_like): current state
            eps (float): epsilon, for epsilon-greedy action selection
        """
        state = torch.from_numpy(state).float().unsqueeze(0).to(device)
        self.q_network_local.eval()
        with torch.no_grad():
            action_values = self.q_network_local(state)
        self.q_network_local.train()
        
        # Epsilon-greedy action selection
        if random.random() > eps:
            return np.argmax(action_values.cpu().data.numpy())
        else:
            return random.choice(np.arange(self.action_size))
        
               
    def soft_update(self, local_model, target_model, tau):
        """Soft update model parameters.
        θ_target = τ*θ_local + (1 - τ)*θ_target

        Params
        ======
            local_model (PyTorch model): weights will be copied from
            target_model (PyTorch model): weights will be copied to
            tau (float): interpolation parameter 
        """
        for target_param, local_param in zip(target_model.parameters(), local_model.parameters()):
            target_param.data.copy_(tau*local_param.data + (1.0-tau)*target_param.data)
        
    def learn(self, experiences, gamma):
        """Update value parameters using given batch of experience tuples.

        Params
        ======
            experiences (Tuple[torch.Variable]): tuple of (s, a, r, s', done) tuples 
            gamma (float): discount factor
        """
        states, actions, rewards, next_states, dones = experiences
        
        # Get max predicted Q values (for next states) from target model
        Q_targets_next = self.q_network_target(next_states).detach().max(1)[0].unsqueeze(1)
        # Compute Q targets for current states
        Q_targets = rewards + (gamma * Q_targets_next * (1-dones))
        
        # Get expected Q values from local model
        Q_expected = self.q_network_local(states).gather(1, actions)
        
        # Compute loss 
        loss = F.mse_loss(Q_expected, Q_targets)
        
        # Minimize the loss 
        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()
        
        self.soft_update(self.q_network_local, self.q_network_target, TAU)
        
        

class ReplayBuffer():
    """ Fixed-size buffer to store experience tuples."""

    def __init__(self, action_size, buffer_size, batch_size, seed):
        """Initialize a ReplayBuffer object.

        Params
        ======
            action_size (int): dimension of each action
            buffer_size (int): maximum size of buffer
            batch_size (int): size of each training batch
            seed (int): random seed
        """
        self.action_size = action_size
        self.memory = deque(maxlen=buffer_size)
        self.batch_size = batch_size
        self.experience = namedtuple("Experience", field_names=['state', 'action', 'reward', 'next_state', 'done'])
        self.seed = random.seed(seed)
        
    def add(self, state, action, reward, next_state, done):
        """Add a new experience to memory"""
        e = self.experience(state, action, reward, next_state, done)
        self.memory.append(e)
    
    def sample(self):
        """Randomly sample a batch of experiences from memory"""
        experiences = random.sample(self.memory, k=self.batch_size)
        
        states = torch.from_numpy(np.vstack([e.state for e in experiences if e is not None])).float().to(device)
        actions = torch.from_numpy(np.vstack([e.action for e in experiences if e is not None])).long().to(device)
        rewards = torch.from_numpy(np.vstack([e.reward for e in experiences if e is not None])).float().to(device)
        next_states = torch.from_numpy(np.vstack([e.next_state for e in experiences if e is not None])).float().to(device)
        dones = torch.from_numpy(np.vstack([e.done for e in experiences if e is not None]).astype(np.uint8)).float().to(device)
        
        return (states, actions, rewards, next_states, dones)
    
    def __len__(self):
        """Return the current size of internal memory"""
        return len(self.memory)

2.2.8 Deep Q-Learning Improvements

• Double DQN:
  Deep Q-Learning tends to overestimate action values. Double Q-Learning has been shown to work well in practice to help with this.

• Prioritized Experience Replay
  Deep Q-Learning samples experience transitions uniformly from a replay memory. Prioritized experienced replay is based on the idea that the agent can learn more effectively from some transitions than from others, and the more important transitions should be sampled with higher probability.

• Dueling DQN
  Currently, in order to determine which states are (or are not) valuable, we have to estimate the corresponding action values for each action. However, by replacing the traditional Deep Q-Network (DQN) architecture with a dueling architecture, we can assess the value of each state, without having to learn the effect of each action.

2.2.9 Double DQN