【机器学习】什么是正则化？如何在线性回归和逻辑回归中使用正则化
系列文章目录
第九章 Python 机器学习入门之正则化
系列文章目录
文章目录
前言
一、正则化
1 什么是正则化？
2 正则化参数 lambda
3 lambda 取值不同，对学习算法有什么影响？
二、如何在线性回归中使用正则化
三、如何在逻辑回归中使用正则化
前言
正则化可以处理过度拟合问题，在线性回归和逻辑回归中均有应用。正则化在线性回归和逻辑回归中也有相似之处，进行梯度下降时的公式都是相似的，只是定义不同。
一、正则化
1 什么是正则化？
使用房子价格的例子，我们使用线性回归想拟合数据，发现只有一个特征时，并不难能好的拟合数据，所以我们添加特征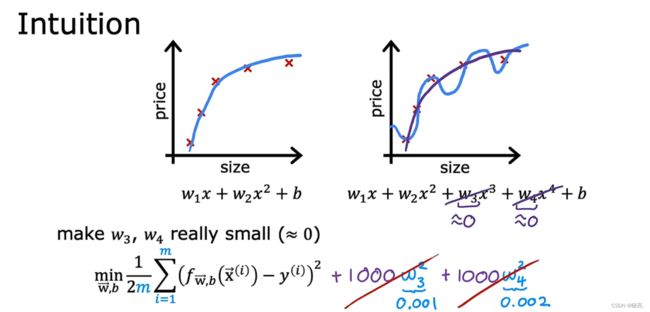
图中左边，当我们有两个特征时，发现可以很好的拟合数据，如果我们继续添加特征
如图中的右边，拟合的是一条曲线，很明显这属于过拟合或高方差，为了解决这个问题，我们可以使用正则化
正则化就是不改变特征的数量，通过改变参数的大小，来使得曲线更好的拟合数据。
图中，如果使得参数w3, w4 接近于0 ，那么拟合的曲线就会接近二次函数了，它可能比二次函数更适合。
2 正则化参数 lambda
前面我们只是使得参数w3, w4 较小，接近于0 ，从而使得模型更加的拟合数据，
但是事实上，如果我们有100个特征，我们不知道哪些时重要特征，哪些是要惩罚的特征，
所以通常实现正则化的方式是惩罚所有的特征，准确来说是惩罚所有的参数w 和 j ，
这会导致拟合更加平滑，简单，不容易过度拟合 
如图，我们通常会惩罚所以的100个特征，使用一个新的值 lambda , 它被称为正则化参数 regularization parameter
与学习速率一样，我们必须给 lambda 选择一个数字 λ > 0，
一般情况下，我们不会因为参数 b 太大而惩罚它，因为是否这样做，我们在实际中得到的结果都是差不多的，当然你也可以选择惩罚参数 b
我们来看看这个修改过后的代价函数，我们希望最小化代价函数，也就是均方差代价加上额外的，
如图，就是均方差代价函数，加上后面额外的 正则化项 regularization term
所以这个新的代价函数权衡了你可能拥有的两个目标
一，尝试最小化均方差代价函数来更好的拟合数据，
二， 尽量减少第二项，使得参数w 保持较小，这会有助于减少过拟合
我们选择的 lambda 值指定了相对重要性 或相对权衡 或者说是我们如何在这两个目标值之间取得平衡
3 lambda 取值不同，对学习算法有什么影响？
还是使用线性回归中房价预测的示例，f(x) 是线性回归模型，
如果 lambda 设置为0，我们这时候就相当于没有使用正则化，因为正则化项为0，拟合的曲线也会过度拟合
如果 lambda 设置为一个非常非常大的值，则等式右边的正则化项就会变得很重要，
最小化这种情况的唯一方法就是确保 参数 w 的所有值都接近于 0 ，这是模型就是拟合成一条直线了，这属于欠拟合或高偏差
所以 lambda 的值太大或太小都不行，它的取值应该适当，
这样才可以平衡新代价函数中的第一项的均方误差代价函数 和第二项的正则化项，保持较小的参数
二、如何在线性回归中使用正则化
用于线性回归的正则化 regularization linear regression
知道了什么是正则化，那如何在梯度下降中使用正则化线性回归呢？
如图这是新的代价函数，我们希望找到参数 w , b 来最小化正则化代价函数
来看看图左边，之前我们对代价函数使用梯度下降，我们反复更新参数w, b ，
其实，正则化线性回归的更新看起来和这个是一样的，处理现在大代价函数 J 的定义有些不同了
改变的是 J 对 w 的求导，如图右边所示，求导后面还加上了正则化项的求导，由于没有正则化参数 b ，所以 J 对 b 的求导不变
将这些导数项写入公式，我们可以得到正则化线性回归的梯度下降算法公式 
跟前面一样，在实现算法时，我们需要保证参数 w , b 同时更新
这里的公式，我们可以使用另一种方法来重写它，如图，可以看见等式的后边就是正常的梯度下降公式，不同的是前面
这里如果α = 0.01，λ = 1，m = 50， 前一段括号里面计算的结果就是0.9998，略小于1
正则化就是让参数 w 乘以一个略小于1 的数，具有收缩的效果
也就是在每次迭代中缩小参数 w 一点点，这就是正则化的工作原理。
迭代公式中的导数的推到过程如图：
三、如何在逻辑回归中使用正则化
用于逻辑回归的正则化 regularized logistic regression
如果我们使用高阶多项式来表示 z ，它会传递到 sigmoid 函数来计算 f ，我们会得到 一个复杂的为训练集拟合的决策边界
如果我们含有多个特征，逻辑回归拟合的决策边界就可能会存在过拟合或高方差风险 
我们来看下逻辑回归的代价函数，如果我们要使用正则化，只需要在等式的后面加上正则化项就可以了，如图
下面来看看最小化这个代价函数
和正则化线性回归的梯度下降一样，正则化逻辑回归的梯度下降也是在导数处有些不同