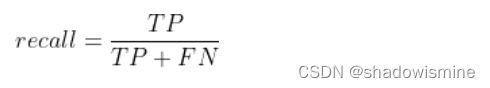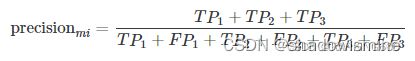常用评价指标及方法（以NILM及SV为例）

1. NILM的评价指标

主要有 accuracy,precision,recal, F1-score, F1-micro, F1-macro

首先需要了解一下几个概念，TP (true positive), FP (false positive), TN (true negitive), FN (false negitive)。

• TP:true positive。预测是正确的正样本
• FP:false positive。预测是错误的正样本
• TN:true negative。预测是正确的负样本
• FP:false positive。预测是错误的负样本

假设存二分类模型使得模型在测试数据集上的结果如下表所示，横坐标为Ground Truth, 纵坐标为预测值：

1.1 准确率 - Accuracy

准确率是指，对于给定的测试数据集，分类器正确分类的样本书与总样本数之比，也就是预测正确的概率。也就是所有数据中，我们正确分类了多少？即:

1.2 精确度 Precision

精确度：以预测结果为判断依据，预测为正例的样本中预测正确的比例。预测为正例的结果分两种，要么实际是正例TP，要么实际是负例FP，则可用公式表示:

精确度还有一个名字，叫做“查准率”，我们关心的主要部分是正例，所以查准率就是相对正例的预测结果而言，正例预测的准确度。直白的意思就是模型预测为正例的样本中，其中真正的正例占预测为正例样本的比例，用此标准来评估预测正例的准确度。

被我们的算法选为positive的数据中，有多少真的是positive的？

1.3 召回率 Recall

召回率：以实际样本为判断依据，实际为正例的样本中，被预测正确的正例占总实际正例样本的比例。实际为正例的样本中，要么在预测中被预测正确TP，要么在预测中预测错误FN，用公式表示：

召回率的另一个名字，叫做“查全率”，评估所有实际正例是否被预测出来的覆盖率占比多少。实际应该为Positive的数据中，多少被我们选为了Positive？

总结：预测时当然希望Precision和Recall都保持一个较高的水准，但事实上这两者在某些情况下是有矛盾的。比如在极端情况下，倘若只搜索出了一个结果，且是正确的，那么Precision就是100%，但是Recall就很低；而如果把所有结果都返回，那么比如Recall是100%，但是Precision就会很低。因此在不同的场合中需要自己判断希望Precision比较高或是Recall比较高，此时可以引出另一个评价指标 F1-Score(F-Measure)。

1.4 F1-score

F1分数（F1 Score）是统计学中用来衡量二分类模型精确度的一种指标，它同时兼顾了分类模型的精确率和召回率。F1分数可以看作是模型精确率和召回率的一种加权平均，它的最大值是1，最小值是0。

数学定义：F1-Score又称为平衡F分数（BalancedScore），它被定义为精确率和召回率的调和平均数。F-score 就是precision 和 recall的 harmonic mean。

总结：直觉上来说TP越大越好，但是这里的大肯定是一个相对的概念，而F-score 就是分别从两个角度，主观（Predicted）和客观（Actual）上去综合的分析TP够不够大。这也就是平常看到的结论 F-score的值 只有在 Precision 和 Recall 都大的时候 才会大。

1.5 宏平均 Macro-F1 、微平均 Micro-F1

在一个多标签分类任务中，可以对每个“类”计算F1，显然需要把所有类的F1合并起来考虑。这里有两种合并方式：

（1）第一种计算出所有类别总的Precision和Recall，然后计算F1。这种方式被称为Micro-F1微平均。

（2）第二种方式是计算出每一个类的Precison和Recall后计算F1，最后将F1平均。这种方式叫做Macro-F1宏平均。

注：微平均 Micro-F1 主要应用在样本数据分布均衡的数据集上，而宏平均Macro-F1 主要应用在样本数据分布不均衡的数据集上，因为它在分类结果中更能照顾小规模样本的权重。

1.6 混淆矩阵（Confusion Matrix）

在机器学习领域，混淆矩阵又称为可能性表格或错误矩阵。它是一种特定的矩阵，用来呈现算法性能的可视化效果，通常是监督学习（非监督学习通常用匹配矩阵：matching matrix）。其每一列代表预测值，每一行代表的是实际的类别。这个名字来源于它可以非常容易的表明多个类别是否有混淆（也就是一个class被预测成另一个class）。

一个二分类（正和反）问题的混淆矩阵如下图所示：

三分类混淆矩阵:

所有正确的预测结果都在对角线上，所以从混淆矩阵中可以很方便直观的看出哪里有错误，因为他们呈现在对角线外面。

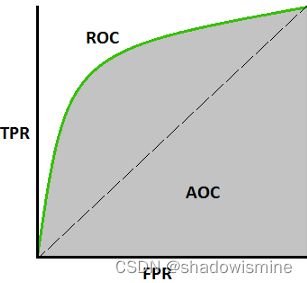
1.7 ROC 曲线

接受者操作特征曲线(Reciver Operating Characteristic Curve,ROC)，用于描述二分类系统性能(分类器阈值是变化的)，反应敏感性和特异性连续变化的综合指标，ROC曲线上的点反应对同一信号刺激的感受性。

用不同的阀值，统计出每组不同阀值下的精确率和召回率：

• x轴为假阳性率（FPR）：在所有的负样本中，分类器预测错误的比例(Specificity) 

• y轴为真阳性率（TPR）：在所有的正样本中，分类器预测正确的比例Sensitivity（等于Recall）

一个典型的 ROC 曲线如下：

为了更好地理解ROC曲线，我们使用具体的实例来说明：

如在医学诊断中,判断有病的样本。那么尽量把有病的揪出来是主要任务，也就是指标TPR，要越高越好。而把没病的样本误诊为有病的，也就是指标FPR，要越低越好。

不难发现,这两个指标之间是相互制约的。如果某个医生对于有病的症状比较敏感，稍微的小症状都判断为有病,那么他的tpr指标应该会很高，但是fpr指标也就相应地变高。最极端的情况下,他把所有的样本都看做有病,那么tpr达到1,fpr指标也为1。

ROC曲线优势就是，当正负样本的分布发生变化时，其形状能够基本保持不变，因此其面积AUC值也适用于不平衡样本。

1.8 AUC（Area Under the Curve，曲线下面积）

AUC是一种模型分类指标，且仅仅是二分类模型的评价指标。

AUC定义：

AUC值为ROC曲线所覆盖的区域面积，显然，AUC越大，分类器分类效果越好。

AUC的物理意义

AUC的物理意义正样本的预测结果大于负样本的预测结果的概率。所以AUC反应的是分类器对样本的排序能力。

另外值得注意的是，AUC对样本类别是否均衡并不敏感，这也是不均衡样本通常用AUC评价分类器性能的一个原因。

2. SV的评价指标

说话人确认（Speaker Verification）的测试阶段需要判断两句话是否来自同一个说话人，或者某句话是否来自某个特定的人，是个二分类问题。

定义：
错误接受率（False Acceptance Rate，FAR）：不该接受的样本（label=0）中被接受（prediction=1）概率

错误拒绝率（False Rejection Rate，FRR）：不该拒绝的样本（label=1）中被拒绝（prediction=0）的概率

2.1 等错误概率EER（Equal Error Rate）

当两个错误概率相等的时候，即 F A R = F R R 时，

EER越小越好。EER认为虚警和漏警对系统影响的代价是相等的，也不关心实际中正例对和负例对的先验概率。

2.2 最小检测代价函数minDCF（Minimum Detection Cost Function）

其中 为错误接受样本（虚警）的风险系数， 为错误拒绝样本（漏警）的风险系数； 和 为正例对和负例对的先验概率，一般来说实际中碰到的绝大部分都是负例对，因此 较小，一般设置为0.01或者0.001。minDCF越小越好。
minDCF考虑了先验概率和不同代价，比 EER 更合理。
在2008年的NIST说话人确认评测中，取  ＝10， ＝1，PT＝0.01，PI＝0.99；在2010年的NIST评测中，取  ＝1，  ＝1，PT＝0.001，PI＝0.999。可见，识别系统要能够应付大量的冒认者，且对错误拒绝更敏感。

2.3 RTF(real_time_factor实时率,在线识别指标)

RTF(real time factor)表示如下：（只找到了ASR的RTF计算方法）

【意义】：平均1秒时长音频给ASR算法需要多少秒处理，小于1才能达到实时效果。越小越好，正常0.2-0.3

即：

原文链接：https://blog.csdn.net/qq_44901949/article/details/124708810