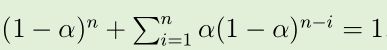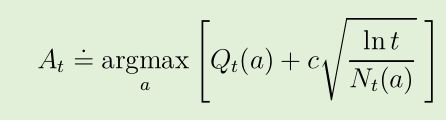强化学习：2.多摇臂赌博机的应用

将强化学习同其他类型的学习区分开来的最重要的特征就是：

• 强化学习使用训练信息来评估所采取的动作, 而非使用正确的动作来指导动作的选择

本章设定——非关联性 nonassocia-tive：仅需要在单个状态下学得如何采取动作——来探讨强化学习评估的方面.

• 这个设定避免了完整强化学习问题的复杂性
• 能清晰地看到评估性反馈怎样地区别于指示性反馈,
• 理解评估性反馈怎样地可以同指示性反馈结合起来.

我们探讨的非关联性的评估性反馈问题正是 k-摇臂赌博机问题 k-armed bandit prob-lem的一种简单形式.

• 下面各部分我们利用这个问题来介绍一些基本的强化学习方法：

2.1 k-摇臂赌博机问题

形式：

• 需要重复地对 k 个不同的选项或动作做出选择.
• 在每一次选择后我们都会获得一个实数型的奖赏, 该奖赏是从固定的概率分布中采样获得的, 且该概率分布取决于所选择的动作.
• 我们的目标是在一定的时期内, 如 1000 个动作选择或时步 time step内, 最大化期望的奖赏和.

k-摇臂赌博机问题中：
q ∗ (a) = E[R t | A t = a].

• 在时步 t 选择的动作记为 A t
• 对应的奖赏记为 R t
• q ∗ (a), 为动作 a 被选择后的期望奖赏

如果你知道了每个动作的值, 那么解决 k-摇臂赌博机问题就很简单了:

• 只要一直选择值最高的动作即可.

但是很多时候并不能确定动作值, 我们需要在探索试错和贪心选择最优中寻找答案
贪心与探索：
贪心greedy动作：

• 如果你维持有对动作值的估计, 那么在任何时步一定至少有一个动作有着最高的估计值. 我们将其称为贪心greedy动作
• 当你选择贪心动作之一时, 我们称你在利用exploit你对动作值的已有知识

探索 explore：

• 非贪心动作能帮助改进对非贪心动作的值的估计
• 探索获取可以在长期内产生更高的奖赏和

平衡问题：

• 在任何一个具体的情况下, 是探索还是利用更好取决于对估计值、不确定性、余下步数的具体值的复杂考量.
• 许多针对 k-摇臂赌博机及其关联问题的特定数学形式的、用于平衡
  探索和利用的精巧方法. 然而, 这些方法中的多数对固定stationarity 及先验知识做出了较强的假设
  • 当这些假设不成立时, 其对最优性的保证或对损失的边界的保证, 都无从谈起.

2.2 动作值方法

动作值方法 action-value method，包括：

• 估计动作值的方法
• 使用估计值来做出动作选择的决策的方法

一种简单的估计方法：

• 估计动作值的样本平均方法 sample-average method
• 动作被选择时的平均奖赏：
  

最简单的动作选择规则：

• 贪心greedy地选择有最高估计值的那个动作
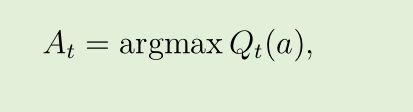
  • 其中 argmax a 表示令后面的表达式最大的那个动作 a(如果有多个最值时任意选择)
• 如果有多于一个的贪心动作, 那么以任意一种方式在选择其中一个, 例如随机选择
  tip：
• 贪心选择总是对已有的知识进行利用来最大化即时的奖赏; 其不会对明显次等的动作进行采样来观察这些动作是否实际上更好.
• 改善上述问题的方法：
  • 在多数的时间内进行贪心选择;
  • 但是每隔一定时间, 如以一个较小的概率 ε, 从所有的动作中以相同的概率进行随机选择, 无论各个动作的估计值为多少.

2.3 10-摇臂测试工具

10-摇臂测试工具：
由 2000 个随机生成的 k -摇臂赌博机问题组成的集合, 其中k = 10

测试贪心方法、ε=0.01贪心方法和ε=0.1贪心方法：

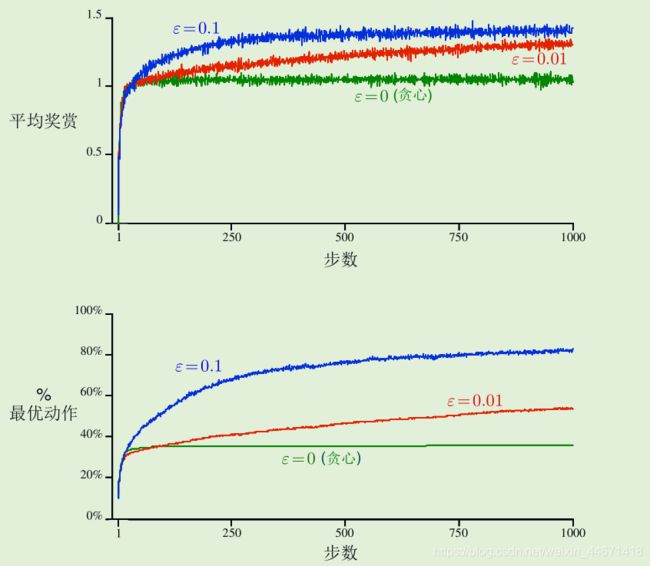
ε-贪心方法对贪心方法的优势视任务而定：

• 假设奖赏的方差变得更大, 对于有更多噪声的奖赏, 代理需要更多的探索来发现最优动作, 那么 ε-贪心方法的优势甚至会更大
• 如果奖赏的方差为 0, 那么贪心方法在试过一次后就可以得知所有动作的真实值. 在这种情况下贪心方法立即发现了最优解, 效果可能是最好的
  • tip： 即使潜在的任务是确定性与固定性的， 强化学习也可能需要对探索与利用进行平衡

2.4 增量式实现

上述讨论的动作值方法都是使用观察到的奖赏的样本均值来估计动作值的：
专注于单个动作上，可写为：

• R i 表示在第 i 次选择该动作后接收到的奖赏
• Q n 表示在选择了 n − 1 次该动作后其估计值

问题：
上式的实现方式就是维持对所有接收到的奖赏的记录, 然后每当需要估计值的时候就计算上方的等式

• 对内存与计算时间的需求会随着越来越多的奖赏被观察到而逐步增大
• 每一个新观察到的奖赏都会需要额外的内存来存储, 需要额外的计算时间来计算分子中的和.

问题解决：增量式地更新均值

• 形式：
  • 新估计值 ← 旧估计值 + 步长[目标 − 旧估计值]
  • (NewEstimate ← OldEstimate + StepSize[Target − OldEstimate])
• 推导：

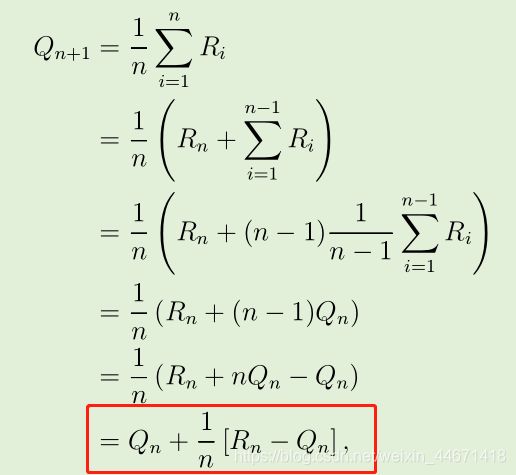
其中，表达式 [目标 − 旧估计值] 是估计中的误差 error.

• 通过向 “目标” 靠近来减小该误差. 目标预示着希望的移动方向, 虽然这可能是有噪声的

2.5 追踪非固定性问题

上述讨论的平均方法可以适用于固定性赌博机问题, 即奖赏的概率分布不会随时间变化的赌博机问题.

• 就像之前指出的那样, 实际上我们经常遇到非固定性的强化学习问题.

①基本思路： 相对于较早的奖赏, 将更多的权重给予较近的奖赏

②方法：使用固定的步长参数，其中步长参数 α ∈ (0,1]
③推导： Q n+1 成为了对过去奖赏与初始估计值 Q 1 的加权平均
加权平均：

• 权重之和为1
• 奖赏 R i 的权重取决于在多少次奖赏前该奖赏被观察到
  • 即 n−1 的值
• 1 − α 的值小于 1, 因此给予 R i 的权重会随着与迄今间隔的奖赏次数增加而减少

随机逼近理论 stochastic approximation theory：
该理论提供了采用合适的步长能以 1 的概率保证收敛的条件:

• 第一个条件来保证这些步长对 “最终克服初始条件或随机波动的影响” 而言足够大
• 第二个条件确保最终步长变得足够小以确保收敛.

采样平均的情形满足上述2条件，而本节的步长恒定的情形并不能满足第二个条件

• 也就是说，估计值不会完全收敛，而是继续随新收到的奖赏变化
  • 这正是非固定性环境所需要的

此外, 满足上述步长参数序列常常收敛得非常缓慢或需要大量的调参来获得令人满意的收敛速率，极少实际应用

2.6 乐观初始值

上述方法都依赖于初始动作的估计值 Q 1 (a)

• 这些方法因初始的估计值产生了偏差 bias
• 对于样本平均方法来说, 当所有的动作都被选择了一次后偏差就消失了
• 但对 α 值恒定的方法来说, 这一偏差会永远存在, 但会随时间逐步减小

在实际应用中, 这类偏差常常并不成问题, 反而有时还很有帮助.

• 其负面影响是初始值实际上变成了一组必须由用户选择的参数
• 其正面影响是提供了一种简单的方式, 来应用关于预期的奖赏值的水平的先验知识.

一种简单的鼓励探索的方式：

• a.故意设置一个极为乐观的初始估计值
• b.使得无论选择何种动作，奖赏都低于初始估计值
• c.学习器因此“失望地”转向其他动作
• d.结果就是所有动作都在估计值收敛前选择数次
  

tip:

• 乐观初始值在在固定性问题上可以表现得非常高效
• 但不适用于非固定性问题, 因为其对探索的驱动本质上是暂时的. 如果任务变化并对探索产生了新的需求, 初始值就没有“乐观”作用了

2.7 上置信界动作选择

贪心动作是当前看上去最好的动作, 但其他动作中的一些可能事实上更好

• 这源于对动作值估计的准确度的不确定性
  • 所以，探索是仍然有必要的

ε-贪心动作选择强制使得非贪婪动作被选择

• 但这一过程对各个动作是不加区分的, 即使是接近贪心或特别不确定的动作也不被偏好.
  • 如果能判断各个非贪心动作成为最优动作的潜力，并根据这个潜力进行动作选择，显然更高效：

上置信界 动作：

• 其中 lnt 表示 t 的自然对数 (e ≈ 2.71828 的该数次幂等于 t)

• N t (a) 表示在时间 t 之前动作 a 被选择的次数

• 常数 c > 0 控制了探索的程度

• 如果 N t (a) = 0, 那么a 被认为是最优动作

动作选择观念： 所有的动作都会被选择, 但有较低的估计值或已经被频繁选择过的动作, 将会随时间推移减少被选择的频率

• 式中的根号项是对 a 的估计值的不确定度或方差
• argmax式中的项 , 是动作 a 可能的真实值的上界的一种, 其中由 c 决定置信水平
• 每当 a 被选择时, 不确定性可以被认为是减少了（N t (a)在分母）
• 每当除 a 之外的动作被选择,t 增加而 N t (a) 保持不变; 因为 t 出现在分子中, 所以对不确定性的估计增加了
• 自然对数的使用意味着增长的速率逐渐变慢, 但其值依然会趋近于无穷大

问题难点：

• 对于非固定性问题的处理复杂
• 需要对巨大状态空间进行处理

2.8 梯度赌博机算法

上文中，我们都是对动作值进行估计，以动作值为依据选择动作
本节的算法中，为每个动作a学习各自实数型的偏好pautoreference, 记为 H t (a).

• 偏好值越高, 那么对应的动作越常被采用

• 但是偏好不能使用奖赏的观念来理解. 只有一个动作相较于另一 个动作的相对偏好值是有意义的;

  • 如果将所有动作的偏好值加上 1000, 各个动作被选择的概率仍然保持不变,

soft-max 分布 (也称为 Gibbs 分布或 Boltzmann分布)：

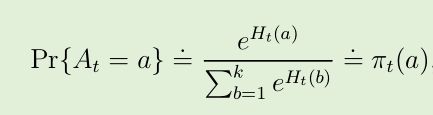
• π t (a), 来表示在时步 t 采取动作 a 的可能性
• 起始时, 所有动作的偏好值都是相等的 H 1 (a) = 0

随机梯度上升 stochastic gradient ascent：
在每一步时, 在选择动作 A t 并收到奖赏 R t 后, 动作偏好值使用下式进行更新:

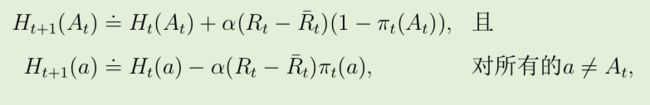
• 上式奖赏的均值为基准线，如果高于基准线，那么采取该动作的概率增加，反之减小

算法表现：

• 所有奖赏的同时增加对梯度赌博机算法绝对没有影响, 因为奖赏的基准线会立即适应到新的水平上.
• 但如果基准线被省略了 , 那么其性能将如图中所示的那样急剧 退化.

2.9 关联搜索 (上下文相关赌博机)

在本节的前面部分, 我们只考虑了非关联任务, 即不需要将不同的动作与不同的情形相关联的任务. 在这种任务中：

• 如果任务是固定性的, 那么学习器试图寻找单个的最佳动作;
• 如果任务是非固定性的, 那么学习器试图随时间的变动追踪最佳的动作.

然而在一般的强化学习任务中, 情形的数量不止一个。大多都是关联搜索 associative search任务的例子

• 既涉及到使用试错来搜索最佳的动作

• 又涉及到将最佳的动作同各自的情形进行关联

2.10 总结

本文中呈现了几种平衡探索与利用的简单方式：

• ε-贪心方法在一小部分时间中随机选择动作
• 而 UCB 方法确定性地进行动作选择，用较少的动作来探索
• 梯度赌博机算法不是对动作值进行估计, 而是对动作偏好进行估计,并使用 soft-max 分布, 以一种分级的、概率性的方式来向更偏好的动作倾斜
• 对估计值进行乐观的初始化这一简单的权宜之计, 使得即使是贪心方法也会进行大量探索
  
  虽然本章中探讨的方法可能是我们目前所能做到的最好的, 但这些远不是 “平衡探索与利用” 这一问题的令人完全满意的解决方案.
• 用于平衡 k-摇臂赌博机问题中的探索与利用的方法, 最好是计算一种被称为基廷斯指数 Gittins index的特殊动作值
• 基廷斯指数方法是贝叶斯 Bayesian 方法的一个实例

Reference：

Reinforcement Learning:An Introduction（second edition）