leetcode - 2849. Determine if a Cell Is Reachable at a Given Time

Description

You are given four integers sx, sy, fx, fy, and a non-negative integer t.

In an infinite 2D grid, you start at the cell (sx, sy). Each second, you must move to any of its adjacent cells.

Return true if you can reach cell (fx, fy) after exactly t seconds, or false otherwise.

A cell’s adjacent cells are the 8 cells around it that share at least one corner with it. You can visit the same cell several times.

Example 1:

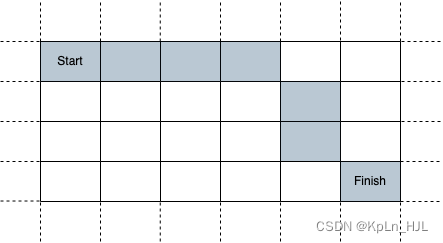
Input: sx = 2, sy = 4, fx = 7, fy = 7, t = 6
Output: true
Explanation: Starting at cell (2, 4), we can reach cell (7, 7) in exactly 6 seconds by going through the cells depicted in the picture above. 

Example 2:

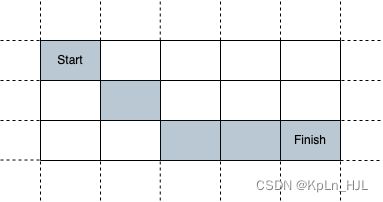
Input: sx = 3, sy = 1, fx = 7, fy = 3, t = 3
Output: false
Explanation: Starting at cell (3, 1), it takes at least 4 seconds to reach cell (7, 3) by going through the cells depicted in the picture above. Hence, we cannot reach cell (7, 3) at the third second.

Constraints:

1 <= sx, sy, fx, fy <= 10^9
0 <= t <= 10^9

Solution

Firstly go diagonal, then go vertical or horizontal to the target.

Go diagonal: min(abs(sx - fx), abs(sy - fy))
Go vertical or horizontal: if horizontal, then abs(sx - fx) - abs(sy - fy), else abs(sy - fy) - abs(sx - fx)

Time complexity: $o(1)$
Space complexity: $o(1)$

Code

class Solution:
    def isReachableAtTime(self, sx: int, sy: int, fx: int, fy: int, t: int) -> bool:
        if sx == fx and sy == fy and t == 1:
            return False
        fastest_time = min(abs(sx - fx), abs(sy - fy)) + abs(abs(sx - fx) - abs(sy - fy))
        return fastest_time <= t