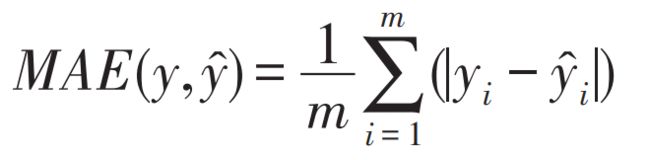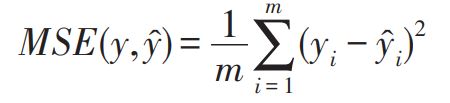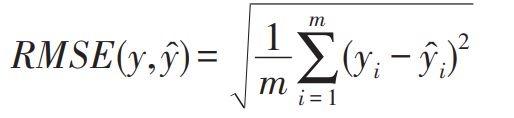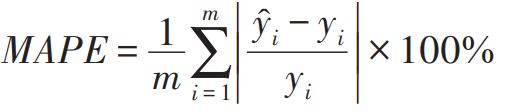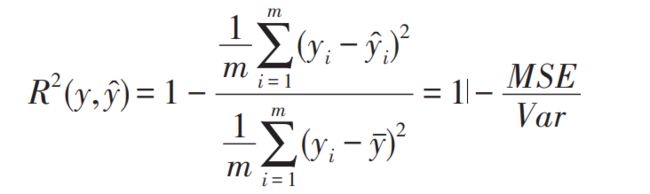时间序列预测(1) — 时间序列预测研究综述

目录

1 什么是时间序列预测?

2 时间序列预测的应用场景与分类

3 时间序列数据的特性

4 时序预测评价指标

5 基于深度学习的时间序列预测方法

5.1 卷积神经网络

5.2 循环神经网络

5.3 Transformer类模型

---

1 什么是时间序列预测?

时间序列：指对某种事物发展变化过程进行观测并按照一定频率采集得出的一组随机变量。
时间序列预测：就是从众多数据中挖掘出其蕴含的核心规律并且依据已知的因素对未来的数据做出准确的估计。

由于大量物联网数据采集设备的接入、多维数据的爆炸增长和对预测精度的要求愈发苛刻，经典的参数模型以及传统机器学习算法难以满足预测任务的高效率和高精度需求。近年来，以卷积神经网络、循环神经网络和 Transformer模型为代表的深度学习算法在时间序列预测任务中取得了丰硕的成果。

2 时间序列预测的应用场景与分类

时间序列数据的研究方向：分类聚类、异常检测、事件预测、时间序列预测等。
时间序列预测的应用场景：时间序列预测通过挖掘时间序列潜在规律，进行类推或者延展用于解决在现实生活中面临的诸多问题，包括噪声消除、股票行情分析、电力负荷预测、交通路况预测、流感疫情预警等。
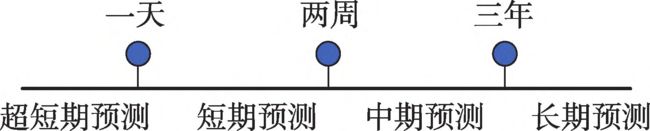
时间序列预测的分类：当时间序列预测任务提供的原始数据仅为目标数据的历史数据时，为单变量时间序列预测，当提供的原始数据包含多种随机变量时，为多变量时间序列预测。时间序列预测任务根据所预测的时间跨度长短，可划分为四类。

3 时间序列数据的特性

时间序列预测是对前 t - 1 个时刻的历史数据学习分析来估计出指定未来时间段的数据值。时间序列数据由于其各变量间固有的潜在联系，常表现出一种或多种特性。

• 海量性：时间序列数据爆炸性增长，在数据集层面进行有效的预处理工作，是高质量完成时间序列预测任务的关键。
• 趋势性：当前时刻数据往往与前一段时刻数据有着密切的联系，该特点暗示了时间序列数据受其他因素影响通常有一定的变化规律，时间序列可能在长时间里展现出一种平稳上升或平稳下降或保持水平的趋势。
• 周期性：时间序列中数据受外界因素影响，在长时间内呈现出起起落落的交替变化。
• 波动性：随着长时间的推移和外部多因素影响，时间序列的方差和均值也可能会发生系统的变化，在一定程度上影响时间序列预测的准确度。
• 平稳性：时间序列数据个别为随机变动，在不同时间上呈统计规律，在方差与均值上保持相对稳定。
• 对称性：若某段时间周期内，原始的时间序列和其反转时间序列的距离控制在一定的阈值以内，曲线基本对齐，即认定该段时间序列具有对称性，例如港口大型运输车往复作业，起重机抬臂和降臂工作等。

4 时序预测评价指标

误差评价指标是衡量一个时间序列预测模型性能的重要方法，一般而言，评价指标计算出的误差越大，模型预测的准确率越低，进而表示所建立的预测模型性能表现也就越差。目前常用的时间序列预测算法评价指标如下：

平均绝对误差（mean absolute error，MAE）：是通过计算每一个样本的预测值和真实值的差的绝对值得出，具体计算公式为：

均方误差（mean square error，MSE）：是一个很实用的指标，通过计算每一个样本的预测值与真实值的差的平方再取平均值得出，具体公式为：

均方根误差（root mean square error，RMSE）：是均方误差进行开方得到，具体公式为：

平均绝对百分比误差（mean absolute percentage error，MAPE）：是相对误差度量值，避免了正误差和负误差相互抵消，具体公式为：

决定系数 R-squared：又叫可决系数（coefficient of determination），也叫拟合优度，其计算结果即为模型预测的准确度，取值范围为[0，1]。 R2 值越接近 1，模型性能越好；该模型等于基准模型时 R2 = 0 ，R-squared公式为：

5 基于深度学习的时间序列预测方法

下面只进行预测方法的简介，可以只看红色字体大致了解，关于具体的代码可以查阅有关资料，后续专栏会逐一介绍原理和代码。

5.1 卷积神经网络

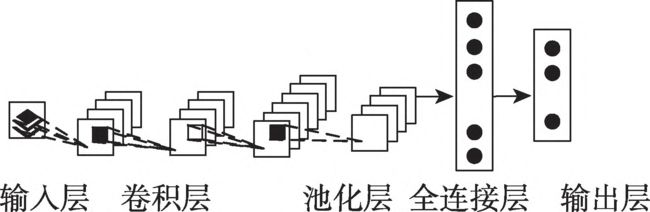
CNN：卷 积 神 经 网 络（convolutional neural networks，CNN）是一类以卷积和池化操作为核心的深层前馈神经网络，在设计之初，其用于解决计算机视觉领域的图片识别问题。卷积神经网络做时间序列预测的原理是利用卷积核的能力，可以感受历史数据中一段时间的变化情况，根据这段历史数据的变化情况做出预测。

CNN 结构示意图 

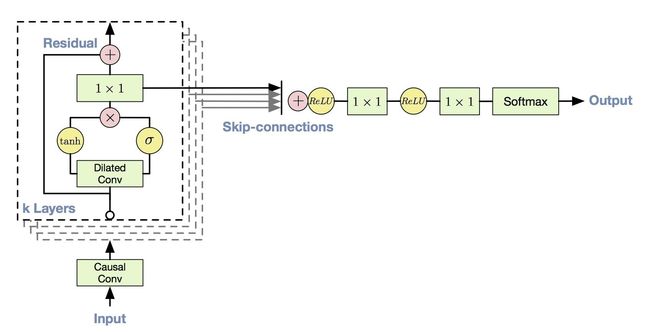
WaveNet-CNN：Borovykh 等受 WaveNet 这种语音序列生成模型的启发，使用 ReLU 激活函数并采用参数化跳过连接，在结构上进行了简化，改进了CNN 模型。该模型在金融分析任务中实现了高性能，证明卷积网络不仅更简单更容易训练，同时在有噪声的预测任务上也能有优异的表现。

WaveNet-CNN 结构示意图  

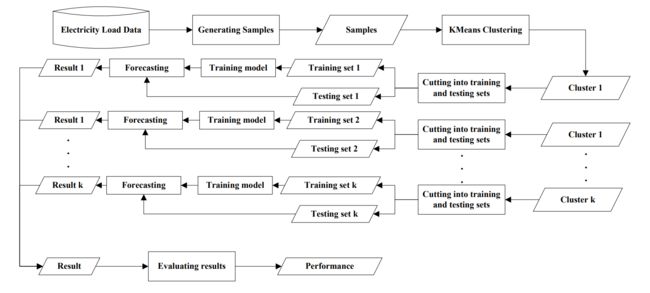
Kmeans-CNN：随着数据集规模越来越大，CNN 在处理大数据集中表现不佳。2017 年，Dong 等选择将可以学习更多有用特征的 CNN 和分割数据的 K 均值聚类算法结合，通过将大数据集中的相似样本聚类，分成多个小样本来训练，在百万级大规模电力负荷数据集中表现良好。

Kmeans-CNN 结构示意图   

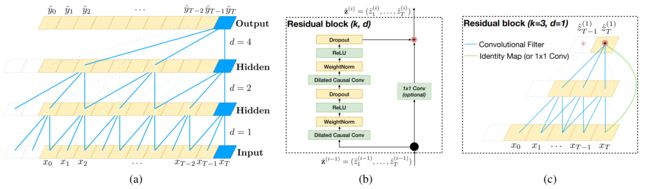
TCN：2018年，Bai等基于 CNN 提出了一种内存消耗更低而且可并行的时间卷积网络架构（temporal convolutional networks，TCN）。TCN 引入因果卷积，保证了未来信息在训练时不会被提前获取到，其反向传播路径与时间方向不同，避免了梯度消失和梯度爆炸问题。为解决 CNN 在层数过多时导致的信息丢失问题，TCN 引入残差连接使得信息在网络间传递时可以跨层传递。

TCN 结构示意图 

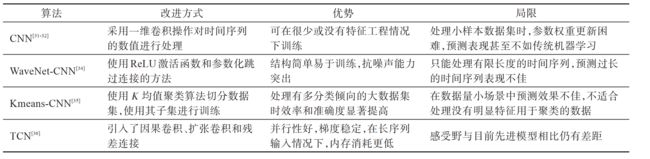
CNN 的预测精度与循环神经网络等其他网络结构相比已不占优势，难以单独处理步长较长的时序预测问题，但常作为一个功能强大的模块接入其他先进算法模型中用于预测任务。卷积神经网络类算法总体分析如下表：

5.2 循环神经网络

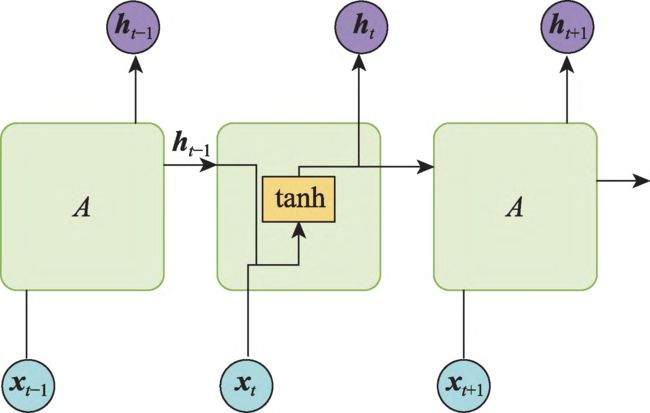
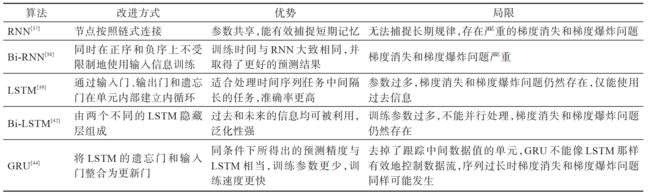
RNN：循环神经网络（recurrent neural networks，RNN）是由 Jordan 在 1990 年提出的用于学习时间维度特征的深度学习模型。RNN 的各单元以长链的形式连接在一起按序列发展的方向进行递归，模型的输入是序列数据。使用 RNN 训练容易出现很严重的梯度消失问题或者梯度爆炸问题。梯度消失问题主要是因为在神经网络模型中位于最前面层的网络权重无法及时进行有效的更新，训练失败；梯度爆炸问题是指由于迭代参数的改变幅度太过剧烈，学习过程不平衡。随着数据长度的提升，该问题愈加明显，导致 RNN 只能有效捕捉短期规律，即仅具有短期记忆。

RNN 结构示意图  

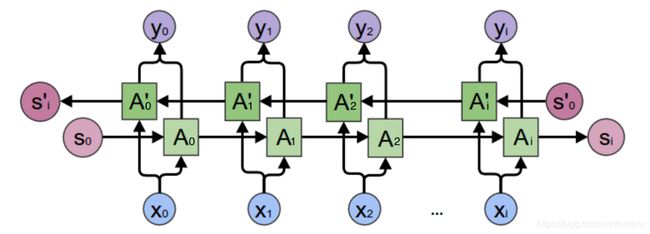
Bi-RNN：1997 年，Schuster等将常规循环神经网络 RNN扩展到双向循环神经网络（bidirectional recurrent neuralnetworks，Bi-RNN）。Bi-RNN 通过同时在前向和后向上训练，不受限制地使用输入信息，直到预设的未来帧，可同时获得过去和未来的特征信息。在人工数据的回归预测实验中，Bi-RNN 与 RNN 训练时间大致相同并取得了更好的预测效果。

Bi-RNN 结构示意图  

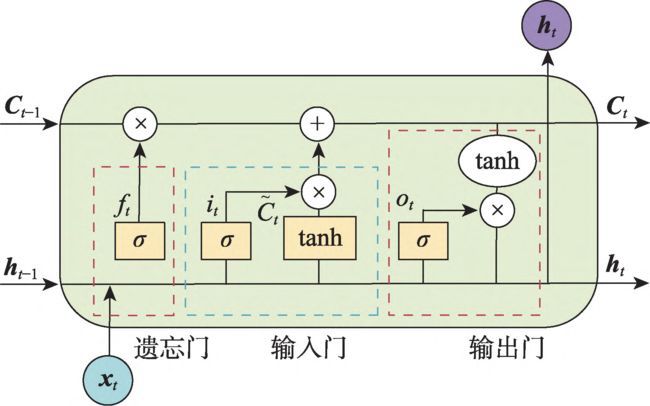
LSTM：长短期记忆网络（long short-term memory，LSTM）于 1997 年被 Hochreiter 提出，用于解决 RNN 模型的诸多问题。

LSTM 结构示意图  

Bi-LSTM：2005年，Graves等[42]提出的双向长短期记忆网络（bidirectional long short-term memory，Bi-LSTM）结构类似于 Bi-RNN，其由两个独立的 LSTM 拼接而成。Bi-LSTM 的模型设计初衷是克服 LSTM 无法利用未来信息的缺点，使 t 时刻所获得特征数据同时拥有过去和将来的信息。由于 Bi-LSTM 利用额外的上下文而不必记住以前的输入，处理较长时间延迟的数据时表现出更强大的能力。经实验表明，没有时间延迟的 LSTM 几乎返回同样的结果，这代表着在部分时间序列数据中向前训练和向后训练两个方向上的上下文同样重要，Bi-LSTM 的特征提取能力明显高
于 LSTM。

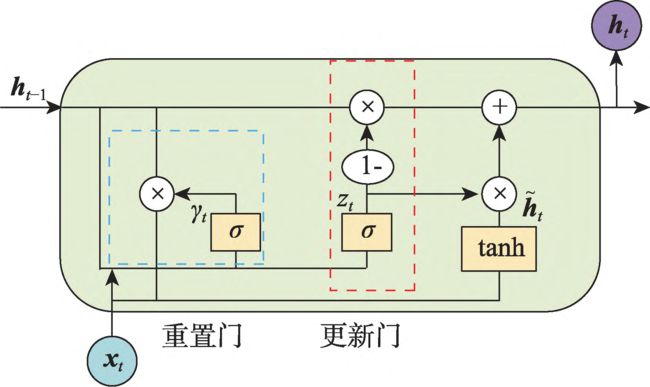
GRU：门控循环单元（gated recurrent unit，GRU）是基于LSTM 模型改进的。

GRU 结构示意图

循环神经网络类方法可以捕获并利用长期和短期的时间依赖关系来进行预测，但在长序列时间序列预测任务中表现不好，并且 RNN 多为串行计算，导致训练过程中对内存的消耗极大，而且梯度消失和梯度爆炸问题始终没有得到彻底解决。循环神经网络类算法总体分析如下：

5.3 Transformer类模型

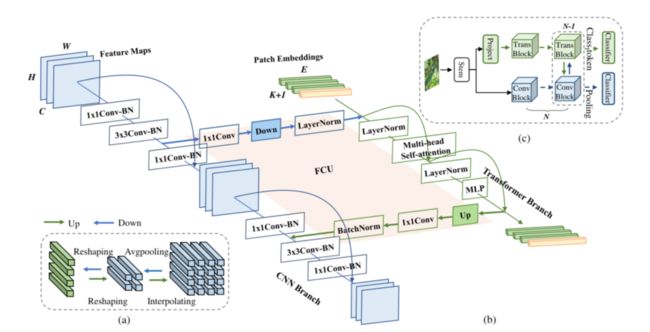
Transformer 这种与以往的CNN 或 者 RNN 结 构 不 同 的 新 的 深 度 学 习 框 架 。Transformer 所采用的自注意力机制所解决的情况是：神经网络的输入是很多大小不一的向量，不同时刻的向量往往存在着某种潜在联系，实际训练的时候无法充分捕捉输入之间的潜在联系而导致模型训练结果较差。

 Transformer结构示意图

Transformer 的核心是自注意力模块，它可以被视为一个完全连接层，其权重是基于输入模式的成
对相似性而动态生成的。其参数数量少，同条件下所需计算量更少，使其适合建模长期依赖关系。
相较于 RNN 的模型，使用 LSTM 和 GRU 也不能避免梯度消失和梯度爆炸的问题：随着网络往后训练，梯度越来越小，要走 n - 1 步才能到第 n 个词，而Transformer的最长路径仅为 1，解决了长期困扰 RNN的问题。Transformer 捕捉长期依赖和彼此交互的突出能力对于时间序列建模任务有巨大吸引力，能在各种时间序列任务中表现出高性能。

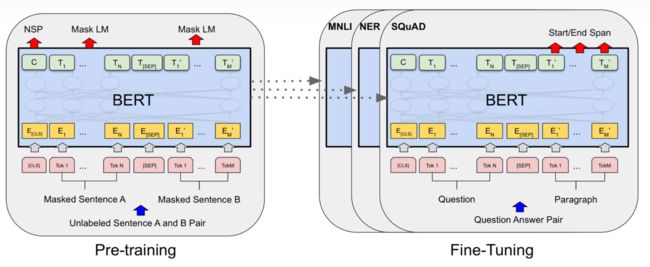
BERT：该模型通过多头自注意力来代替预测任务常用的 RNN 来捕获时间序列信息，还通过分解嵌入参数化来更有效地确定每个时间步之前和之后状态之间的自相关性，只需要有关交通速度和一周内几天的道路信息，不需要当前时刻相邻道路的流量信息，应用局限性小。

BERT结构示意图 

AST：应用生成对抗思想在 SparseTransformer基础上提出了对抗稀疏 Transformer（adversarial sparse Transformer，AST）。

Informer：北京航空航天大学的在经典的 Transformer 编码器-解码器结构的基础上提出了Informer 模型来弥补 Transformer 类深度学习模型在应用于长序列时间预测问题时的不足。在此之前，解决预测一个长序列的任务往往采用多次预测的方法，而 Informer 可以一次给出想要的长序列结果，Informer具体结构如图所示：

Informer 结构示意图 

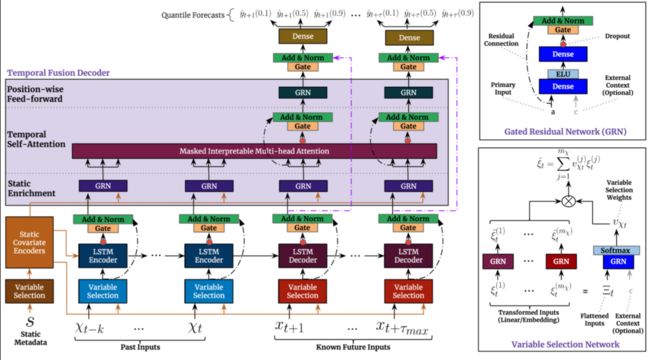
TFT： TFT（temporal fusiontransformers）设计了一个包含静态协变量编码器、门控特征选择模块和时间自注意力解码器的多尺度预测模型。

TFT 结构示意图  

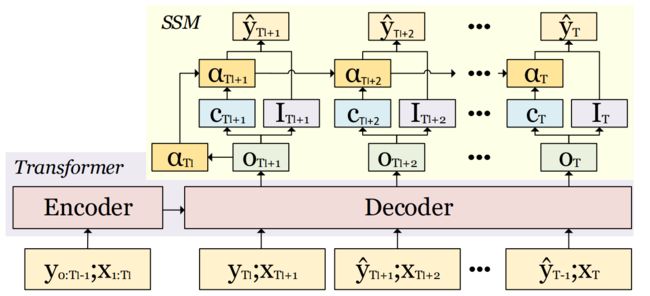
SSDNet：空间状态空间分解神经网络（state space decomposition neural network，SSDNet），将 Transformer 深度学习架构和状态空间模型（statespace models，SSM）相结合，兼顾了深度学习的性能优势和 SSM 的可解释性。SSDNet 采用 Transformer 架构来学习时间模式并直接估计SSM的参数。为了便于解释，使用固定形式的 SSM 来提供趋势和周期性成分以及 Transformer的注意力机制，以识别过去历史的哪些部分对预测最重要。

SSDNet 结构示意图 

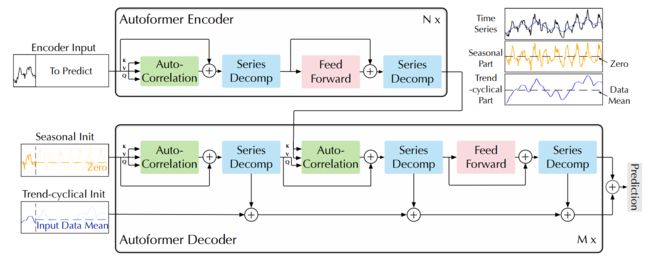
Autoformer：设计了一种简单的周期性趋势分解架构。Autoformer 继承使用Transformer的编码器-解码器结构。通过 Autoformer采用的独特内部算子能够将变量的总体变化趋势与预测的隐藏变量分离，这种设计可以使模型在预测程中交替分解和细化中间结果。

SSDNet 结构示意图  

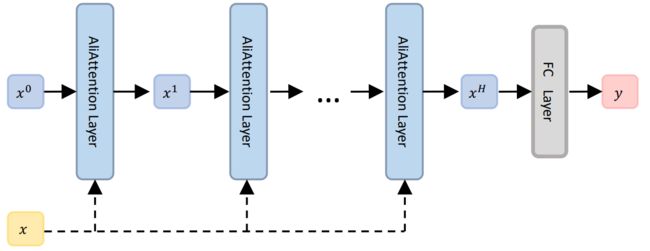
Aliformer：2021 年，阿里巴巴为解决电子商务中准确的时间序列销售预测问题，提出基于双向 Transformer 的 Aliformer，利用历史信息、当前因素和未来知识来预测未来的数值。Aliformer设计了一个知识引导的自注意力层，使用已知知识的一致性来指导时序信息的传输，并且提出未来强调训练策略，使模型更加注重对未来知识的利用。

Aliformer 结构示意图 

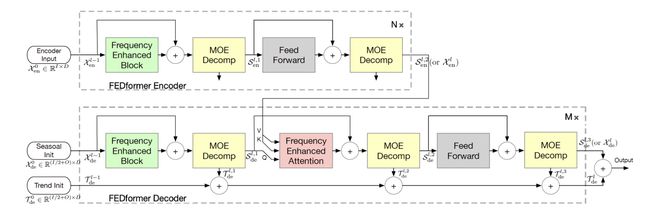
FEDformer：2022 年提出的 FEDformer（frequencyenhanced decomposed Transformer）设计了两个注意模块，分别用傅里叶变换[68]和小波变换[69]处理频域中应用注意力操作。FEDformer 将广泛用于时间序列分析的周期性趋势分解方法融入到基于 Transformer 的方法中，还将傅里叶分析与基于 Transformer 的方法结合起来，没有将 Transformer应用于时域，而是将其应用于频域，这有助于 Transformer 更好地捕捉时间序列的全局特征。

FEDformer 结构示意图 

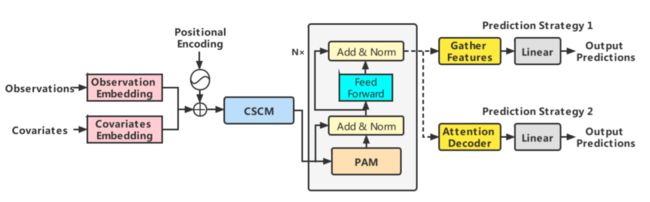
Pyraformer：2022 年提出 Pyraformer，这是一种基于金字塔注意力的新型模型，可以有效地描述短期和长期时间依赖关系，且时间和空间复杂度较低。

Pyraformer 结构示意图  

Conformer：2023年为解决有明显周期性的长序列预测任务的效率和稳定性问题，提出了一种针对多元长周期时序预测的 Conformer模型。

Conformer 结构示意图   

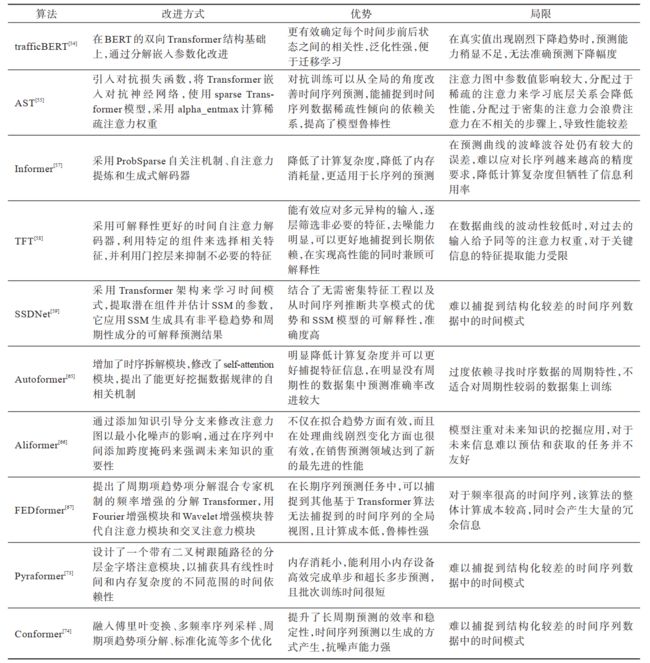
Transformer 类算法如今广泛用于人工智能领域的各项任务，在 Transformer 基础上构建模型可以打破以往算法的能力瓶颈，可以同时具备良好的捕捉短期和长期依赖的能力，有效解决长序列预测难题，并且可以并行处理。上述算法性能对比和总体分析如下：

 参考论文：深度学习应用于时序预测研究综述