飞桨图像分类

---

一、图像分类数学知识前置

1.矩阵加法运算

1、理论

I2 = I1 + b
1.1 如果I1和b维度一致时，结果为两个矩阵对应项相加。
1.2 如果I1和b维度不一致，但是满足一定条件，亦可进行加法计算。
假设I1的矩阵形状为shape_I1=（h,w,c）,那么在b的矩阵形状shape_b为shape_I1的某个切片相等时，I1和b矩阵可以进行“广播”相加。

2、代码实现

## 矩阵加减法
import numpy as np
I1 = [[j*4+i for i in range(4)] for j in range(4)]
I1 = np.array(I1,dtype='float32')
b = 0.2
I2 = I1 + b

value = {}
value['I1'] = I1
value['b'] = b
value['I2'] = I2
print("I1={I1},\nb={b},\nI2={I2}\n".format(**value))

b = [[0.2 for i in range(4)] for j in range(4)]
b = np.array(b,dtype='float32')
I2 = I1 + b
value = {}
value['I1'] = I1
value['b'] = b
value['I2'] = I2
print("I1={I1},\nb={b},\nI2={I2}\n".format(**value))

b = np.random.uniform(0,1,(4,4))
I2 = I1 + b
value = {}
value['I1'] = I1
value['b'] = b
value['I2'] = I2
print("I1={I1},\nb={b},\nI2={I2}\n".format(**value))

I1=[[ 0.  1.  2.  3.]
 [ 4.  5.  6.  7.]
 [ 8.  9. 10. 11.]
 [12. 13. 14. 15.]],
b=0.2,
I2=[[ 0.2  1.2  2.2  3.2]
 [ 4.2  5.2  6.2  7.2]
 [ 8.2  9.2 10.2 11.2]
 [12.2 13.2 14.2 15.2]]

I1=[[ 0.  1.  2.  3.]
 [ 4.  5.  6.  7.]
 [ 8.  9. 10. 11.]
 [12. 13. 14. 15.]],
b=[[0.2 0.2 0.2 0.2]
 [0.2 0.2 0.2 0.2]
 [0.2 0.2 0.2 0.2]
 [0.2 0.2 0.2 0.2]],
I2=[[ 0.2  1.2  2.2  3.2]
 [ 4.2  5.2  6.2  7.2]
 [ 8.2  9.2 10.2 11.2]
 [12.2 13.2 14.2 15.2]]

I1=[[ 0.  1.  2.  3.]
 [ 4.  5.  6.  7.]
 [ 8.  9. 10. 11.]
 [12. 13. 14. 15.]],
b=[[0.02066405 0.56324786 0.10918893 0.52730695]
 [0.14764967 0.74266    0.19208365 0.12315764]
 [0.52998913 0.28110296 0.76049194 0.64685051]
 [0.38987322 0.33829646 0.00499981 0.36445759]],
I2=[[ 0.02066405  1.56324786  2.10918893  3.52730695]
 [ 4.14764967  5.74266     6.19208365  7.12315764]
 [ 8.52998913  9.28110296 10.76049194 11.64685051]
 [12.38987322 13.33829646 14.00499981 15.36445759]]

2.矩阵和数乘法运算

1、理论

I3 = a * I1
I1各个元素分别乘以a

2、代码实现

## 矩阵和数的乘法
import numpy as np
I1 = [[j*4+i for i in range(4)] for j in range(4)]
I1 = np.array(I1,dtype='float32')
a = 0.2
I2 = I1 * a

value = {}
value['I1'] = I1
value['a'] = a
value['I2'] = I2
print("I1={I1},\na={a},\nI2={I2}\n".format(**value))

I1=[[ 0.  1.  2.  3.]
 [ 4.  5.  6.  7.]
 [ 8.  9. 10. 11.]
 [12. 13. 14. 15.]],
a=0.2,
I2=[[0.        0.2       0.4       0.6      ]
 [0.8       1.        1.2       1.4      ]
 [1.6       1.8000001 2.        2.2      ]
 [2.4       2.6000001 2.8       3.       ]]

3.矩阵乘法运算

1、理论

I2 = I1 * A

1. 二维矩阵
   I1的r行向量与A的c列向量的点积作为I3的（r,c）元素
2. 多维矩阵
   所得结果的后两维的shape与二维矩阵的计算方式一致。不同的是高维度（3位以上）的尺寸大小的计算方式-取较大的尺寸。作为多维矩阵，数据还是保持在后两维中，高维度只是数据的排列方式的定义。本质上，高维矩阵的乘法还是二维矩阵之间的乘法，再加上排列方法的保持，当高维尺寸不同时，只要可以“广播”，就依然可以计算。
   譬如：
   2.1 I1的shape为 (c,n,s),A的shape为（c，s，m）时，I2的shape为（c,n,m).
   结果shape的计算过程：I1的后两维shape为（n,s), A的后两维shape为（s,m),类似于二维矩阵乘法所得结果的后两维shape为（n,m), 高维度的尺寸取c。
   2.2 I1的shape为 (n,c,h,s),A的shape为（1,1，s，w）时，I2的shape为（n,c,h,w).
   结果shape的计算过程：I1的后两维shape为（h,s), A的后两维shape为（s,m),类似于二维矩阵乘法所得结果的后两维shape为（h,w), 高维度的尺寸取（n,c）和（1,1）中尺寸较大值（n,c）。

2、代码实现

import numpy as np


I1 = [[j*4+i for i in range(4)] for j in range(4)]
I1 = np.array(I1,dtype='float32')
A = np.random.uniform(0,1,(4,4))

## 二维矩阵乘法 1
I2 = np.matmul(I1,A)
## 二维矩阵乘法 2
I3 = np.zeros_like(I2)
for i in range(4):
    for j in range(4):
        I3[i,j] = np.dot(I1[i,:],A[:,j])

value = {}
value['I1'] = I1
value['a'] = A
value['I2'] = I2
value['I3'] = I3
print("I1={I1},\na={a},\nI2={I2}\n".format(**value))
print("I1={I1},\na={a},\nI3={I2}\n".format(**value))
print("I2 ==I3: {}\n".format(np.allclose(I2,I3)))

## 高维矩阵乘法
## (3,100,9) , (3,9,99)
I1 = np.random.uniform(0,1,(3,100,9))
A = np.random.uniform(0,1,(3,9,99))
I2 = np.matmul(I1,A)
value = {}
value['I1'] = I1
value['A'] = A
value['I2'] = I2
#print("I1={I1},\na={a},\nI2={I2}\n".format(**value))
print("I1 shape={},A shape={},I2 shape={}".format(I1.shape,A.shape,I2.shape))

## 高维矩阵乘法
## (100,3,100,9) , (1,3,9,99)
I1 = np.random.uniform(0,1,(100,3,100,9))
A = np.random.uniform(0,1,(1,3,9,99))
I2 = np.matmul(I1,A)
value = {}
value['I1'] = I1
value['A'] = A
value['I2'] = I2
#print("I1={I1},\na={a},\nI2={I2}\n".format(**value))
print("I1 shape={},A shape={},I2 shape={}".format(I1.shape,A.shape,I2.shape))

I1=[[ 0.  1.  2.  3.]
 [ 4.  5.  6.  7.]
 [ 8.  9. 10. 11.]
 [12. 13. 14. 15.]],
a=[[0.40225179 0.40187989 0.80693188 0.26112979]
 [0.38977539 0.23862796 0.77949091 0.91098417]
 [0.25046811 0.87720739 0.08533057 0.17098334]
 [0.86682769 0.52630865 0.31773004 0.41900392]],
I2=[[ 3.49119469  3.57196868  1.90334217  2.50996261]
 [11.12848664 11.74806422  9.86127577  9.55836749]
 [18.76577858 19.92415977 17.81920938 16.60677238]
 [26.40307052 28.10025531 25.77714298 23.65517727]]

I1=[[ 0.  1.  2.  3.]
 [ 4.  5.  6.  7.]
 [ 8.  9. 10. 11.]
 [12. 13. 14. 15.]],
a=[[0.40225179 0.40187989 0.80693188 0.26112979]
 [0.38977539 0.23862796 0.77949091 0.91098417]
 [0.25046811 0.87720739 0.08533057 0.17098334]
 [0.86682769 0.52630865 0.31773004 0.41900392]],
I3=[[ 3.49119469  3.57196868  1.90334217  2.50996261]
 [11.12848664 11.74806422  9.86127577  9.55836749]
 [18.76577858 19.92415977 17.81920938 16.60677238]
 [26.40307052 28.10025531 25.77714298 23.65517727]]

I2 ==I3: True

I1 shape=(3, 100, 9),A shape=(3, 9, 99),I2 shape=(3, 100, 99)
I1 shape=(100, 3, 100, 9),A shape=(1, 3, 9, 99),I2 shape=(100, 3, 100, 99)

4.算子

传统计算机视觉利用算子，以及算子集对进行图像处理，从而获得特征图像，CNN中的卷积核即是与之相对应的概念。不同是，前者需要算法开发者手动设计，而后者通过训练数据的驱动来自动选择，而且通常情况下CNN网络中的卷积核数量远超过手动设计的。

Sobel算子
Laplace算子

5.卷积

该过程可理解为算子（核）窗口在图像上沿指定维度滑动，同时将矢量点积值作为对应输出矩阵元素的值。 举例如下：

6.求导法则

我们定义
自变量y为标量，y为向量，y=$\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right]$,Y为矩阵，Y= $\left[\begin{array}{cccc}{y}_{11}& y_{12}& \cdots & y_{1n}\\ y_{21}& y_{22}& \cdots & y_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ y_{m1}& y_{m2}& \cdots & y_{mn}\end{array}\right]$,

自变量x为标量，x为向量，x=$\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_p\end{array}\right]$,X为矩阵，X=$\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1q}\\ x_{21}& x_{22}& \cdots & x_{2q}\\ ⋮& ⋮& \ddots & ⋮\\ x_{p1}& x_{p2}& \cdots & x_{pq}\end{array}\right]$。

1. y(x)’ --标量关于向量的导数,这是我们熟悉的偏导数,包含m个元素。

y(x)’= $\left[\begin{array}{cccc}\frac{\partial y}{\partial x_1}& \frac{\partial y}{\partial x_2}& \cdots & \frac{\partial y}{\partial x_p}\end{array}\right]$

2. y(X)’ --标量关于向量的导数,这是我们熟悉的偏导数,包含m个元素。

y(X)’= $\left[\begin{array}{cccc}\frac{\partial y}{\partial x_{11}}& \frac{\partial y}{\partial x_{21}}& \cdots & \frac{\partial y}{\partial x_{p1}}\\ \frac{\partial y}{\partial x_{12}}& \frac{\partial y}{\partial x_{22}}& \cdots & \frac{\partial y}{\partial x_{p2}}\\ \frac{\partial y}{\partial x_{1q}}& \frac{\partial y}{\partial x_{2q}}& \cdots & \frac{\partial y}{\partial x_{pq}}\end{array}\right]$

3. Y(x)’ --矩阵关于标量x的求导,逐个元素求导，包含m*n个元素。

Y(x)’= $\left[\begin{array}{cccc}\frac{\partial y_{11}}{\partial x}& \frac{\partial y_{12}}{\partial x}& \cdots & \frac{\partial y_{1n}}{\partial x}\\ \frac{\partial y_{21}}{\partial x}& \frac{\partial y_{22}}{\partial x}& \cdots & \frac{\partial y_{2n}}{\partial x}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial y_{m1}}{\partial x}& \frac{\partial y_{m2}}{\partial x}& \cdots & \frac{\partial y_{mn}}{\partial x}\end{array}\right]$

4. y(x)’ --向量关于向量x的求导，可以理解为"1"的组合形式，包含m*p个元素。

y(x)’= $\left[\begin{array}{cccc}\frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}& \cdots & \frac{\partial y_1}{\partial x_p}\\ \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2}& \cdots & \frac{\partial y_2}{\partial x_p}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial y_m}{\partial x_1}& \frac{\partial y_m}{\partial x_2}& \cdots & \frac{\partial y_m}{\partial x_p}\end{array}\right]$

5. Y(X)’ --矩阵关于矩阵X的导数,与“3”类似，将矩阵Y和X转换为等价向量，再求导，共包含m*n*p*q个元素。

向量化矩阵可以表示为：
vec(Y) = $\left[\begin{array}{ccccc}{Y}_{11}& \cdots Y_{m1}{Y}_{12}& \cdots Y_{m2}& \cdots Y_{1n}& \cdots Y_{mn}\end{array}\right]$ ,
vec(X) = $\left[\begin{array}{ccccc}{X}_{11}& \cdots X_{p1}{X}_{12}& \cdots X_{p2}& \cdots X_{1q}& \cdots X_{pq}\end{array}\right]$ .

那么，
Y(X)’=vec(F)(vec(X))’ = …

公式太长了，具体表达式就不写了，请参照第3种情况。

7.反向传播

深度学习有一个假设，当网络描述了数据分布时，损失函数处于全局极值点。

观测上图，当我们身处群山之中，即使无法得到完整的地势地貌信息y（x），也可以通过观测所处位置的坡度（y(x)’），沿坡度方向用脚丈量并找到下山的路径–最优x。对于神经网络，一个直观的理解–当深度神经网络的表达式(y=f(w,x))比较复杂，我们难以直接进行参数（w）求解时，可以沿梯度下降方向迭代逼近网络第i个节点的参数最优解。
ps.此处w,x可以为向量或者矩阵。

8.MNIST

MNIST数据库（Modified National Institute of Standards and Technology database）是一个大型数据库的手写数字是通常用于训练各种图像处理系统。该数据库还广泛用于机器学习领域的培训和测试。它是通过“重新混合” NIST原始数据集中的样本而创建的。创作者认为，由于NIST的培训数据集来自美国人口普查局员工，而测试数据集则来自美国 高中学生，这不是非常适合于机器学习实验。此外，将来自NIST的黑白图像归一化以适合28x28像素的边界框并进行抗锯齿处理，从而引入了灰度级。
包含60,000个训练图像和10,000个测试图像。训练集的一半和测试集的一半来自NIST的训练数据集，而训练集的另一半和测试集的另一半则来自NIST的测试数据集。数据库的原始创建者保留了一些经过测试的方法的列表。在他们的原始论文中，他们使用支持向量机获得0.8％的错误率。类似于MNIST的扩展数据集EMNIST已于2017年发布，其中包含240,000个训练图像和40,000个手写数字和字符的测试图像。 MNIST手写数字识别模型的主要任务是：输入一张手写数字的图像，然后识别图像中手写的是哪个数字。 该模型的目标明确、任务简单，数据集规范、统一，数据量大小适中，在普通的PC电脑上都能训练和识别，堪称是深度学习领域的“Hello World!”，学习AI的入门必备模型。

9.Imagenet

简介
ImageNet项目是一个用于视觉对象识别软件研究的大型可视化数据库。超过1400万的图像URL被ImageNet手动注释，以指示图片中的对象;在至少一百万个图像中，还提供了边界框。ImageNet包含2万多个类别; 一个典型的类别，如“气球”或“草莓”，包含数百个图像。第三方图像URL的注释数据库可以直接从ImageNet免费获得;但是，实际的图像不属于ImageNet。自2010年以来，ImageNet项目每年举办一次软件比赛，即ImageNet大规模视觉识别挑战赛（ILSVRC），软件程序竞相正确分类检测物体和场景。 ImageNet挑战使用了一个“修剪”的1000个非重叠类的列表。2012年在解决ImageNet挑战方面取得了巨大的突破，被广泛认为是2010年的深度学习革命的开始。

数据集
ImageNet就像一个网络一样，拥有多个Node（节点）。每一个node相当于一个item或者subcategory。据官网消息，一个node含有至少500个对应物体的可供训练的图片/图像。它实际上就是一个巨大的可供图像/视觉训练的图片库。 ImageNet的结构基本上是金字塔型：目录->子目录->图片集。 该数据库首次作为一个海报在普林斯顿大学计算机科学系的研究人员在佛罗里达州举行的2009年计算机视觉与模式识别（CVPR）会议上发布。 ImageNet对其注释过程进行了众包。 图像级注释表示图像中存在或不存在对象类，例如“此图像中有老虎”或“此图像中没有老虎”。 对象级注释提供了指定对象（的可见部分）周围的边界框。 ImageNet使用广泛的WordNet架构的变体来对对象进行分类，增加了120种类别的狗品种以展示细粒度的分类。WordNet使用的一个缺点是这些类别可能比ImageNet最适合的“提升”：“大多数人对Lady Gaga或iPod Mini比对这种罕见的双龙座更感兴趣。” 2012年，ImageNet是Mechanical Turk的全球最大学术用户。 普通工人每分钟识别50张图像。

ImageNet挑战
自2010年以来，每年度ImageNet大规模视觉识别挑战赛（ILSVRC），研究团队在给定的数据集上评估其算法，并在几项视觉识别任务中争夺更高的准确性。 ILSVRC旨在“追踪2005年建立的规模较小的PASCAL VOC挑战”，该挑战仅包含大约20000个图像和20个目标类别。 ILSVRC使用仅包含1000个图像类别或“类别”的“修剪”列表，其中120个品种中有90个由完整的ImageNet架构分类。 2010年在图像处理方面取得了显着进展。 2011年左右，ILSVRC分类错误率为25%。 2012年，深卷积神经网络达到了16%;在接下来的几年中，错误率下降到几个百分点。虽然2012年的突破是“前所未有的组合”，但大幅量化的改进标志着全行业人工智能繁荣的开始。到2015年，研究人员报告说，软件在狭窄的ILSVRC任务中超出人类能力。然而，作为挑战组织者之一的Olga Russakovsky在2015年指出，这些计划只需将图像识别为属于千分之一的图像;人类可以识别更多的类别，并且（不像程序）可以判断图像的上下文。 到2014年，超过50家机构参加了ILSVRC。2015年，百度科学家因使用不同帐户而被禁止使用一年，大大超过每周两次提交的指定限制。百度后来表示，它解雇了涉及的团队领导，并建立了一个科学咨询小组。 2017年，38个竞争团队中有29个错误率低于5%。 2017年，ImageNet宣布将在2018年推出一项新的，更加困难的挑战，其中涉及使用自然语言对3D对象进行分类。由于创建3D数据比注释预先存在的2D图像更昂贵，数据集预计会更小。这方面的进展应用范围从机器人导航到增强现实。 2017年11月前后，谷歌的AutoML项目发展出新的神经网络拓扑结构，创建了NASNet，这是一个针对ImageNet和COCO优化的系统。 据Google称，NASNet的性能超过了以前发布的所有ImageNet性能。

10.批归一化（Batch Normalization）Batch normalization applies a transformation that maintains the mean output close to 0 and the output standard deviation close to 1.

Importantly, batch normalization works differently during training and during inference.

During training (i.e. when using fit() or when calling the layer/model with the argument training=True), the layer normalizes its output using the mean and standard deviation of the current batch of inputs. That is to say, for each channel being normalized, the layer returns (batch - mean(batch)) / (var(batch) + epsilon) * gamma + beta, where: epsilon is small constant (configurable as part of the constructor arguments) gamma is a learned scaling factor (initialized as 1), which can be disabled by passing scale=False to the constructor. beta is a learned offset factor (initialized as 0), which can be disabled by passing center=False to the constructor.

During inference (i.e. when using evaluate() or predict() or when calling the layer/model with the argument training=False (which is the default), the layer normalizes its output using a moving average of the mean and standard deviation of the batches it has seen during training. That is to say, it returns (batch - self.moving_mean) / (self.moving_var + epsilon) * gamma + beta.

self.moving_mean and self.moving_var are non-trainable variables that are updated each time the layer in called in training mode, as such:

moving_mean = moving_mean * momentum + mean(batch) * (1 - momentum) moving_var = moving_var * momentum + var(batch) * (1 - momentum) As such, the layer will only normalize its inputs during inference after having been trained on data that has similar statistics as the inference data.

1.为什么要采用BN？

随着神经网络的层数加深，研究者发现神经网络训练起来越困难，收敛越慢。BN就是为解决这一问题提出的。 首先明确神经网络之所以可以先训练，再预测并取得较好效果的前提假设：神经网络的训练数据和测试数据是独立同分布的 在神经网络的训练过程中，如果输入数据的分布不断变化，神经网络将很难稳定的学习规律，这也是one example SGD训练收敛慢的原因(随机得到的数据前后之间差距可能会很大)。而网络的每一层通过对输入数据进行线性和非线性变换都会改变数据的分布，随着网络层数的加深，每层接收到的数据分布都不一样，这还怎么学习规律呀，这就使得深层网络训练困难。

BN的启发来源是：之前的研究表明如果在图像处理中对输入图像进行白化操作的话(所谓白化，就是对输入数据分布变换到0均值，单位方差的正态分布)那么神经网络会较快收敛。神经网络有很多隐藏层，图像只是第一层的输入数据，对于每一个隐藏层来说，都有一个输入数据，即前一层的输出。BN将每一层的输入都进行了类似于图像白化的操作，将每层的数据都控制在稳定的分布内，并取得了很好的效果。

2.怎么进行BN？

BN算法是专门针对mini-batch SGD进行优化的，mini-batch SGD一次性输入batchsize个数据进行训练，相比one example SGD，mini-batch SGD梯度更新方向更准确，毕竟多个数据的分布和规律更接近整体数据的分布和规律，类似于多次测量取平均值减小误差的思想，所以收敛速度更快。

3.BN的本质思想 BN究竟对数据的分布做了什么处理，我们来看下面的示意图：

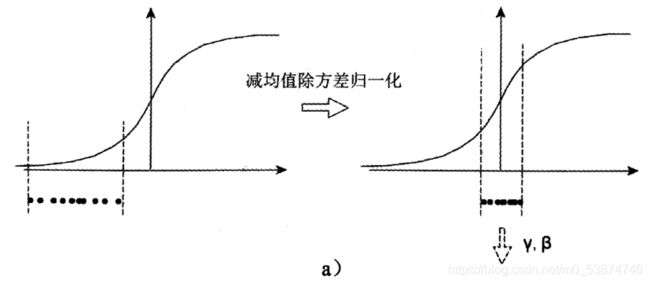
在概率论中我们都学过，数据减去均值除以方差后，将变成均值为0，方差为1的标准正态分布。如果数据分布在激活函数(图中假设为sigmoid)梯度比较小的范围，在深层神经网络训练中将很容易出现梯度消失的现象，这也是深度网络难训练的原因。通过规范化处理后的数据分布在0附近，图中为激活函数梯度最大值附近，较大的梯度在训练中收敛速度自然快。

但是，关键问题出现了，分布在0附近的数据，sigmoid近似线性函数，这就失去了非线性激活操作的意义，这种情况下，神经网络将降低拟合性能，如何解决这一问题呢？作者对规范化后的(0,1)正态分布数据x又进行了scale和shift操作：y = scale * x + shift，即对(0,1)正态分布的数据进行了均值平移和方差变换，使数据从线性区域向非线性区域移动一定的范围，使数据在较大梯度和非线性变换之间找到一个平衡点，在保持较大梯度加快训练速度的同时又不失线性变换提高表征能力。这两个参数需要在训练中由神经网络自己学习，即公式中的γ和β。如果原始数据的分布就很合适，那么即使经过BN，数据也可以回到原始分布状态，这种情况下就相当于恒等变换了，当然这是特殊情况。

11.感受野

在卷积神经网络中，感受野（Receptive Field）的定义是卷积神经网络每一层输出的特征图（feature map）上每个像素点在原始图像上映射的区域大小，这里的原始图像是指网络的输入图像，是经过预处理（如resize，warp，crop）后的图像。

神经元之所以无法对原始图像的所有信息进行感知，是因为在卷积神经网络中普遍使用卷积层和pooling层，在层与层之间均为局部连接。

神经元感受野的值越大表示其能接触到的原始图像范围就越大，也意味着它可能蕴含更为全局，语义层次更高的特征；相反，值越小则表示其所包含的特征越趋向局部和细节。因此感受野的值可以用来大致判断每一层的抽象层次.

感受野的计算
如图所示8X8的原始图像，经过kernel_size=3, stride=2的Conv1，kernel_size=3, stride=1的Conv2后，输出特征图大小为2X2，很明显，原始图像的每个单元的感受野为1，Conv1的每个单元的感受野为3，而由于Conv2的每个单元都是由3X3范围的Conv1构成，因此回溯到原始图像，每个单元能够看到大小7X7的区域范围。

参数量
Conv1的参数量为3X3=9, Conv2的参数量为3X3=9，总参数量为18。两层卷积的感受野为7X7，其感受野等价于参数量为49的kernel_size=7卷积，但是两者的参数却相差了巨大。这给了我们一个启示，通过使用组合的kernel代替较大的单一kernel，可以降低网络参数，但却不会显著减弱网络的感知能力。

几篇参考文献

1. 关于LeNet的前世今生

2. 常用网络结构

3. GoogleNet解析

4. 你必须要知道CNN模型：ResNet

5. Alexnet论文

6. GoogleNet论文

7. Resnet论文

二、图像分类

1.图像分类竞赛全流程工具

• 编程语言
    python
• 炼丹框架
    PaddlePaddle2.0
• 图像预处理库
    OpenCV
    PIL(pillow)
• 通用库
    Numpy
    Pandas
    Scikit-Learn
    Matplotlib

2、图形处理

1.EDA（Exploratory Data Analysis）与数据预处理

1.1 数据EDA
  探索性数据分析（Exploratory Data Analysis，简称EDA），是指对已有的数据（原始数据）进行分析探索，通过作图、制表、方程拟合、计算特征量等手段探索数据的结构和规律的一种数据分析方法。一般来说，我们最初接触到数据的时候往往是毫无头绪的，不知道如何下手，这时候探索性数据分析就非常有效。
  对于图像分类任务，我们通常首先应该统计出每个类别的数量，查看训练集的数据分布情况。通过数据分布情况分析赛题，形成解题思路。（洞察数据的本质很重要。）
数据分析的一些建议
1、写出一系列你自己做的假设，然后接着做更深入的数据分析。
2、记录自己的数据分析过程，防止出现遗忘。
3、把自己的中间的结果给自己的同行看看，让他们能够给你一些更有拓展性的反馈、或者意见。（即open to everybody）
4、可视化分析结果

# 导入所需要的库

import os
import pandas as pd
import numpy as np
from PIL import Image

import paddle
import paddle.nn as nn
from paddle.io import Dataset
import paddle.vision.transforms as T
import paddle.nn.functional as F
from paddle.metric import Accuracy

import warnings
warnings.filterwarnings("ignore")

# 数据EDA
df = pd.read_csv('data/data71799/lemon_lesson/train_images.csv')
d=df['class_num'].hist().get_figure()
d.savefig('2.jpg')

1.2 数据预处理
Compose实现将用于数据集预处理的接口以列表的方式进行组合。

# 定义数据预处理
data_transforms = T.Compose([
    T.Resize(size=(32, 32)),
    T.Transpose(),    # HWC -> CHW
    T.Normalize(
        mean=[0, 0, 0],        # 归一化
        std=[255, 255, 255],
        to_rgb=True)    
])

2.图像标准化与归一化

  最常见的对图像预处理方法有两种，一种叫做图像标准化处理，另外一种方法叫做归一化处理。数据的标准化是指将数据按照比例缩放,使之落入一个特定的区间。将数据通过去均值，实现中心化。处理后的数据呈正态分布,即均值为零。数据归一化是数据标准化的一种典型做法,即将数据统一映射到[0,1]区间上。

作用

1. 有利于初始化的进行
2. 避免给梯度数值的更新带来数值问题
3. 有利于学习率数值的调整
4. 加快寻找最优解速度

标准化

归一化

没有归一化前,寻找最优解的过程&归一化后的过程

3、Baseline选择

  理想情况中，模型越大拟合能力越强，图像尺寸越大，保留的信息也越多。在实际情况中模型越复杂训练时间越长，图像输入尺寸越大训练时间也越长。
比赛开始优先使用最简单的模型（如ResNet），快速跑完整个训练和预测流程；分类模型的选择需要根据任务复杂度来进行选择，并不是精度越高的模型越适合比赛。
在实际的比赛中我们可以逐步增加图像的尺寸，比如先在64 * 64的尺寸下让模型收敛，进而将模型在128 * 128的尺寸下训练，进而到224 * 224的尺寸情况下，这种方法可以加速模型的收敛速度。

Baseline应遵循以下几点原则：

1. 复杂度低，代码结构简单。
2. Loss收敛正确，评价指标（metric）出现相应提升（如accuracy/AUC之类的）
3. 迭代快速，没有很复杂（Fancy）的模型结构/Loss function/图像预处理方法之类的
4. 编写正确并简单的测试脚本，能够提交submission后获得正确的分数

4、模型训练

标签平滑（LSR）

  在分类问题中，一般最后一层是全连接层，然后对应one-hot编码，这种编码方式和通过降低交叉熵损失来调整参数的方式结合起来，会有一些问题。这种方式鼓励模型对不同类别的输出分数差异非常大，或者说模型过分相信他的判断，但是由于人工标注信息可能会出现一些错误。模型对标签的过分相信会导致过拟合。
标签平滑可以有效解决该问题，它的具体思想是降低我们对于标签的信任，例如我们可以将损失的目标值从1稍微降到0.9，或者将从0稍微升到0.1。总的来说，标签平滑是一种通过在标签y中加入噪声，实现对模型约束，降低模型过拟合程度的一种正则化方法。
论文地址 飞桨2.0API地址

$\widetilde{y_k}=(1-ϵ)\ast y_k+ϵ\ast {\mu }_k$

其中 1−ϵ 和 ϵ 分别是权重，$\widetilde{y_k}$是平滑后的标签，通常 μ 使用均匀分布。
学习率调整策略

为什么要进行学习率调整？

  当我们使用梯度下降算法来优化目标函数的时候，当越来越接近Loss值的全局最小值时，学习率应该变得更小来使得模型尽可能接近这一点。

可以由上图看出，固定学习率时，当到达收敛状态时，会在最优值附近一个较大的区域内摆动；而当随着迭代轮次的增加而减小学习率，会使得在收敛时，在最优值附近一个更小的区域内摆动。（之所以曲线震荡朝向最优值收敛，是因为在每一个mini-batch中都存在噪音）。因此，选择一个合适的学习率，对于模型的训练将至关重要。下面来了解一些学习率调整的方法。

针对学习率的优化有很多种方法，而linearwarmup是其中重要的一种。

飞桨2.0学习率调整相关API

当我们使用梯度下降算法来优化目标函数的时候，当越来越接近Loss值的全局最小值时，学习率应该变得更小来使得模型尽可能接近这一点，而余弦退火（Cosine annealing）可以通过余弦函数来降低学习率。余弦函数中随着x的增加余弦值首先缓慢下降，然后加速下降，再次缓慢下降。这种下降模式能和学习率配合，以一种十分有效的计算方式来产生很好的效果。

5、预测模型

https://aistudio.baidu.com/aistudio/course/introduce/11939?directly=1&shared=1