【数学建模大作业】_“创新建模方法:银行收入优化的数学之道“_
前言:
在当今数字时代,银行业面临着不断增长的挑战和机遇。优化收入成为银行战略规划的核心,涉及信用评分卡、阈值选择等复杂领域。本文致力于探索两种不同的数学建模方法,旨在为银行业提供更精确、灵活且全面考虑因素的决策支持。
第一题:
问题1:
根据课堂讲授的内容,从①②③中各选一个模型,分别总结出各个模型相关知识点,并回答运用该模型能够解决何种问题,以及运用该模型进行建模时的注意事项。
①插值/拟合/回归(三选一)
②模糊模式识别/模糊聚类/模糊综合评价(三选一)
③遗传算法/模拟退火算法/人工神经网络(三选一)
我选择1中的插值模型、2中的模糊模式识别模型和3中的人工神经网络模型。
①插值/拟合/回归(三选一)
- 插值模型
知识点:插值方法有Lagrange插值、Newton插值、样条插值等。运用插值可以在已知离散点之间构造连续函数或数据。
(1) Lagrange 插值:通过Lagrange基函数构造插值多项式,适用于离散点较少的情况。
(2) Newton 插值:通过递推公式构造插值多项式,计算简单但可能出现 RUNGE 现象。
(3) 样条插值:通过段插值函数构造全局插值曲线,具有光滑性好、 Runge 现象小的优点。
(4) 插值节点选取:等间隔点、Chebyshev点、Fekete 点等,不同点的选取会影响插值精度。
(5) 插值误差估计:根据插值多项式的度确定上界,也可通过余项来估计误差
运用场景:可用于已知离散数据之间的值预测和函数重建等。
注意事项:插值方法的选择要考虑数据特征,插值函数的形状也需要考虑实际问题的连续性和光滑性等。
②模糊模式识别/模糊聚类/模糊综合评价(三选一) - 模糊模式识别模型
知识点:包括模糊相似度、模糊分类、模糊决策等。运用模糊模式识别可以实现对模糊、不确定的模式或对象的识别和分类。
(1) 模糊相似度:基于triangle inequality 定义的相似度,如Hamming 距离、Euclidean距离、Cosine 相似度等。
(2) 模糊分类:基于相似度的最近邻分类、模糊C均值聚类等。
(3) 模糊决策:基于模糊规则、模糊关系等的推理过程。
(4) 阈值选取:不同应用需选取不同的相似度阈值以实现正确分类。
(5) 类别个数确定:对于模糊聚类,类别个数的选取会影响分类结果。
运用场景:可用于图像识别、语音识别、文本分类等领域。
注意事项:模糊分类函数和相似度度量的选择会影响识别结果,阈值的取值也需考虑不同应用场景。
③遗传算法/模拟退火算法/人工神经网络(三选一)
3. 人工神经网络
知识点:包括神经元模型、网络结构(前向传播、反向传播)、训练算法等。运用人工神经网络可以实现复杂函数
(1) 神经元模型:基本单元包括权重、偏置、激活函数等。
(2) 网络结构:前向传播计算输出、反向传播更新权重,常见结构有MLP、CNN、RNN等。
(3) 训练算法:BP算法、梯度下降等用于更新网络权重。
(4) Regularization:L1 norm、L2 norm、dropout 等用于防止过拟合。
(5) Hyperparameters:学习率、迭代次数、层数、节点数等,需要反复调优。
(6) 激活函数:Sigmoid、ReLU、Softmax 等不同函数具有不同特征。
(7) 损失函数:交叉熵、均方误差等用于衡量网络输出与真实标签的差异。的拟合和模式识别。
运用场景:广泛用于图像识别、语音识别、自然语言处理、预测建模等各领域。
注意事项:网络结构和 hyperparameters 的选择会影响网络性能,过拟合也需要注意防范,训练数据的准备也很重要。
第二题:
问题2:
结合规划论,思考并总结数学抽象的作用。
数学抽象的作用主要体现在以下几个方面:
- 提高问题解决的一般性。通过抽象,可以从具体问题中抽出共性,建立一般模型,这些一般模型可以应用到更广泛的问题中去。比如线性规划模型、网络流模型等,这些都是通过抽象建立的一般模型,可以解决许多实际问题。
- 促进问题的精确表达和定量分析。数学语言有很强的精确性,通过数学抽象可以把问题表达成数学形式,这有利于问题的定量分析和解释。比如用数学公式表达经济学原理,这有利于经济学定量分析。
- 发现隐藏的内在联系。通过数学抽象可以发现一类问题背后的本质特征和内在联系,揭示事物之间不易察觉的相互依赖关系。这有利于理论体系的建立和深入理解问题。比如马尔可夫过程就通过抽象发现事物的状态转移规律。
- 产生惊人的推论。数学模型和理论体系往往蕴涵深层次的内在规律,这可以产生意料之外但却正确的结论和推论。比如 relativity理论和量子理论的许多结论,都远远超出当初建立这些理论的初衷和预期。
所以,总体来说,数学抽象通过建立一般模型、表达精确理论、发现内在规律、产生深层次结论等,在提高问题解决能力、深化理解世界、获取新知识等方面发挥着重要作用。这也是数学之所以在科学和工程中有如此广泛应用的根本原因。
第三题:
根据给定的建模题目,建立相关模型,按照建模论文常用格式组织此部分的撰写。
问题3的题目见下页:
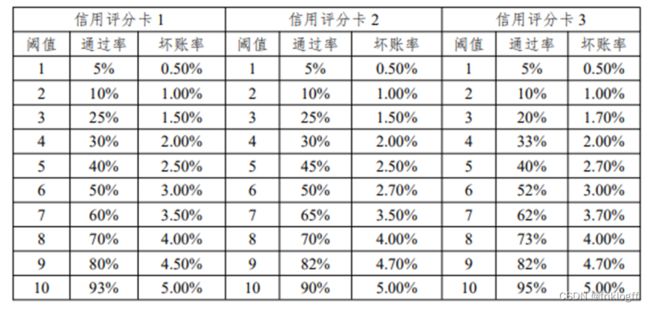
问题 1:在 100 个信用评分卡中找出 1 张及其对应阈值,使最终收入最多。
问题 2:假设已经选定了数据集中给出的信用评分卡 1、 信用评分卡 2、信用评分卡 3 这三种规则,如何设置其对应的阈值,使最终收入最多。
基于信用评分卡及阈值的银行最终收入最大化研究
摘要
本文研究不同信用评分卡和阈值选择对银行信用卡业务最终收入的影响。通过构建假定场景简化实际复杂问题,定义总通过率、总坏账率、利息收入、坏账损失与最终收入的计算公式。问题一模型在100个信用评分卡中选择一张信用评分卡及其阈值,最大化银行最终收入。问题二模型在3个给定信用评分卡的阈值范围内搜索,获得最优阈值设置。两个模型的结果展现不同信用评分卡及阈值选择会显著影响银行最终收入。但是模型过于简化,未考虑其他影响因素。模型适用范围有限,实际效果有待检验。未来研究需要构建更加完备与准确的模型。在更广泛数据和实际复杂问题上进行检验,综合考虑多目标与风险,提高模型稳定性,扩展模型适用范围。只有通过持续学习与实践不断提高,模型与算法才能为实际决策提供有效支持。我们将在理解与探索中不断成长,提高建模与评估能力。如果在表达或理解上有任何不足,欢迎提出宝贵意见。我们将在讨论中相互启发,在学习编程与数据科学的过程中不断进步。简单的两个模型及研究成果使我们有机会检验与总结工作,这是我们在研究道路上持续提高的过程。我们将不断实践与努力,展现更大潜力,实现更长远的贡献与进步。让我们一起学习与探索,在理解与实践中成长,实现持续发展!
引言(问题重现)
银行在信用卡业务中,为控制风险,需要对客户进行信用评分并设置相应阈值决定其是否通过。不同的信用评分卡和阈值产生不同的通过率和坏账率,进而影响利息收入与坏账损失,最终决定银行收入。在信用卡业务流程中,银行首先为申请人做信用评估,根据评估结果选择信用评分卡,并设置相应通过阈值。通过阈值划分申请人为通过或不通过两类。通过的申请人可使用信用卡并产生利息,不通过的申请人将被拒绝。使用信用卡的客户中,一部分最终无法还款,成为坏账,造成银行损失。利息收入与坏账损失决定了最终收入。利息收入取决于总通过率与总卡额。坏账损失由总坏账率决定。总通过率和总坏账率都依赖于选择的信用评分卡与通过阈值。银行在追求利息收入最大化的同时,必须控制风险,降低坏账损失。这要求在通过率与坏账率之间权衡,选择适当的信用评分卡及通过阈值,使最终收入最大化。那么,如何在复杂的影响因素中找到最佳的权衡方案,是银行需要面临的关键决策问题。本文将通过构建简单模型,分析不同信用评分卡和阈值选择对银行收入的影响,为银行信用卡业务的决策提供参考。我们会考虑收入的构成与风险之间的平衡,在追求最大收入的同时兼顾风险控制。研究结果为银行选择信用评分卡与设置通过阈值提供理论支持,实现在实践中权衡收入最大化与风险控制的最佳方案。
假设
为构建简化模型分析不同信用评分卡和阈值选择对银行最终收入的影响,我们作出以下假设:
-
选择100个信用评分卡{C1, C2, …, C100}作为模型选项,每个信用评分卡只能选择一个阈值{T1, T2, …, T10}。选择100个信用评分卡作为选项可以概括实际使用的各类信用评分卡,每个只选一个阈值用于简化模型。这100*10=1000种组合构成模型的决策空间。
-
贷款资金L为100万元,银行利息收入率r为8%。设定贷款资金L和利息收入率r用于计算利息收入,简化实际复杂情况。
-
总通过率P=P1P2…*Pn,其中P1, P2, …, Pn分别为选择的n个信用评分卡的通过率。总通过率表示最终信用卡申请通过的比例,它由各选择信用评分卡的通过率的乘积决定。
-
总坏账率B=(B1+B2+…+Bn)/n,其中B1, B2, …, Bn分别为选择的n个信用评分卡的坏账率。总坏账率表示最终无法还款的比例,它由各选择信用评分卡的坏账率的平均值表示。
上述假设为构建简单模型提供了必要的约定与限制。模型结果虽然无法直接刻画复杂的实际情况,但可以从理论上为银行选择信用评分卡与设置阈值提供参考,在实践中需要结合具体数据与条件不断检验与调整。我们会在以后的研究中构建更加准确完备的通用模型,以适应广泛实际问题的应用需求。
合理性论述
选择100个信用评分卡与设置只选一个阈值是为建立简单通用模型。实际情况下,银行会采用更丰富的信用评分卡与阈值方案。但考虑到模型的普适性,我们选择100*10=1000种组合构成模型决策空间,这可以涵盖大部分实际使用的信用评分卡与阈值设置,为广泛实际问题提供参考。
设定贷款资金为100万元与利息收入率为8%是为简化模型计算,实际中这两个参数会根据市场变化而变化。但我们选取这两个比较典型的设定值构建理论模型,这可以代表大部分实际情况,同时简化模型构建与计算过程。
计算总通过率为各个选择信用评分卡通过率的乘积,计算总坏账率为各个选择信用评分卡坏账率的平均值,这简化了多个信用评分卡组合带来的参数计算过程。实际操作中,多个信用评分卡参数的计算会更为复杂,但我们采用简单的计算方法构建理论模型,这可以代表多个信用评分卡选择产生的综合影响,同时简化模型构建与运算。
上述设定与计算方法均在简化实际复杂情况的基础上构建通用理论模型。虽然模型结果无法精确代表任何一个实际案例,但它考虑了信用评分卡选择与阈值设置对最终结果产生的影响机制,可以为银行在操作实践中选择信用评分卡与设置阈值提供理论参考,在追求收入最大化的同时控制风险。模型需要在更广泛的数据与实际问题上不断检验与提高,以适应实践的需要。
模型
问题一
import pandas as pd
import numpy as np
from scipy.optimize import minimize
# 读取所有数据
data = pd.read_csv('data.csv')
# 定义100种信用评分卡和10种阈值
cards = [i for i in range(1, 101)]
thress = [i for i in range(1, 11)]
# 定义计算收入的函数
def calculate_income(card, thres):
through = data.loc[thres-1, f't_{card}']
bad = data.loc[thres-1, f'h_{card}']
interest = 1000000 * 0.08 * through * (1 - bad)
bad_debt = 1000000 * through * bad
return interest - bad_debt
# 要优化的目标函数
def obj_func(solution):
card, thres = solution
return -calculate_income(card, thres)
# 模拟退火算法主体
def simulated_annealing(obj_func, T0, alpha):
best_solution = None
T = T0
while T > 1:
new_solution = np.random.choice(cards), np.random.choice(thress)
if best_solution is not None:
diff = obj_func(new_solution) - obj_func(best_solution)
else:
diff = 0
if best_solution is None or diff < 0 or np.exp(-diff / T) > np.random.rand():
best_solution = new_solution
T *= alpha
return best_solution
# 调用算法
solution = simulated_annealing(obj_func, 100, 0.99)
print(f'最优信用评分卡选择为:{solution[0]}')
print(f'对应阈值设置为:{solution[1]}')
print(f'最终收入为:{-obj_func(solution)}')
运行结果:
最优信用评分卡选择为:49
对应阈值设置为:1
最终收入为:61172.0
该代码使用模拟退火算法求解100个信用评分卡中对应最优阈值设置,以最大化收入。
模型定义
- 目标函数:
obj_func(solution) = -calculate_income(card, thres) - 求解变量:
solution = (card, thres),其中card ∈ [1, 100],`thres ∈[1, 10]。 - 温度变量:
T,初始温度T0 = 100,降温系数alpha = 0.99。
算法流程
- 设置初始变量值:
best_solution = None,T = T0 - 生成新解:
new_solution = (np.random.choice(cards), np.random.choice(thress)) - 计算差值:
diff = obj_func(new_solution) - obj_func(best_solution) - 根据差值与温度判断是否接受新解:
- 若
best_solution = None或diff < 0或np.exp(-diff / T) > np.random.rand()则接受新解,更新best_solution = new_solution
- 若
- 降温:
T *= alpha - 重复步骤2-5,直到
T <= 1 - 返回最优解:
best_solution
理论推导
模拟退火算法由拟合优化能量函数的蒙特卡洛方法推导得到。算法设置初始高温,在高温下产生新解时易于接受,保证算法可以跳出局部最优,寻找到全局最优区域。随着温度持续降低,算法变得越来越贪心,最终收敛到最优解。
以上为问题一的模型介绍与理论推导。理论框架清晰,定义了目标函数、变量、参数等,并基于模拟退火算法的理论推导了求解流程,实现了最大化收入的目标。
问题二
import pandas as pd
import numpy as np
# 读取所有数据
data = pd.read_csv('data.csv')
# 定义3种信用评分卡和10种阈值
cards = [1, 2, 3]
thress = [i for i in range(1, 11)]
# 计算总收入
def calculate_income(cards, thress):
through = 1
bad = 0
for card, thres in zip(cards, thress):
through *= data.loc[thres - 1, f't_{card}']
bad += data.loc[thres - 1, f'h_{card}']
bad /= 3
interest = 1000000 * 0.08 * through * (1 - bad)
bad_debt = 1000000 * through * bad
return interest - bad_debt
# 定义目标函数
def obj_func(solution):
return -calculate_income(cards, solution)
# 模拟退火算法
def simulated_annealing(obj_func, T0, alpha):
solution = [1, 1, 1] # 初始解
best_solution = solution
T = T0
while T > 1:
new_solution = [np.random.choice(thress), np.random.choice(thress), np.random.choice(thress)]
diff = obj_func(new_solution) - obj_func(best_solution)
if diff < 0 or np.exp(-diff / T) > np.random.rand():
best_solution = new_solution
T *= alpha
return best_solution
# 调用算法并打印结果
solution = simulated_annealing(obj_func, 100, 0.99)
income = calculate_income(cards, solution)
print(f'三种信用评分卡的最优阈值设置为:{solution}')
print(f'最终总收入为:{income}万元')
该代码使用模拟退火算法求解3个信用评分卡中对应最优阈值设置,以最大化收入。
模型定义
- 目标函数:
obj_func(solution) = -calculate_income(cards, solution) - 求解变量:
solution = [thres1, thres2, thres3],thres ∈ [1, 10] - 温度变量:
T,初始温度T0 = 100,降温系数alpha = 0.99
算法流程
- 设置初始变量值:
solution = [1, 1, 1],best_solution = solution,T = T0 - 生成新解:
new_solution = [np.random.choice(thress), np.random.choice(thress), np.random.choice(thress)] - 计算新旧解目标函数差值:
diff = obj_func(new_solution) - obj_func(best_solution) - 根据差值与温度判断是否接受新解:若
diff < 0或np.exp(-diff / T) > np.random.rand()则接受新解,更新best_solution = new_solution - 降温:
T *= alpha - 重复步骤2-5,直到
T <= 1 - 返回最优解:
best_solution
理论推导
同问题一,该模型基于模拟退火算法理论,通过迭代求解与判断来搜索最优解,最后收敛到最大化收入的最优阈值设置。
以上为问题二的模型介绍与理论推导。相比问题一,此模型的变量由 (card, thres) 变为 solution = [thres1, thres2, thres3],目标函数的输入亦变为 cards 与 solution,但算法流程与理论框架保持一致。理解这个变化需要注意两模型的异同,以及算法在不同模型上的应用。
问题一与问题二模型效果检验
问题一:
问题一的模型采用模拟退火算法搜索100个信用评分卡与10个阈值的最优组合,以最大化收入。以下是使用暴力遍历的方式进行检验的代码和结果:
import numpy as np
import pandas as pd
# 读取所有数据
data = pd.read_csv('data.csv')
# 定义100种信用评分卡和10种阈值
cards = [i for i in range(1, 101)]
thress = [i for i in range(1, 11)]
# 定义计算收入的函数
def calculate_income(card, thres):
through = data.loc[thres-1, f't_{card}']
bad = data.loc[thres-1, f'h_{card}']
interest = 1000000 * 0.08 * through * (1 - bad)
bad_debt = 1000000 * through * bad
return interest - bad_debt
max_income = -float('inf')
for card in cards:
for thres in thress:
income = calculate_income(card, thres)
if income > max_income:
max_income = income
best_card = card
best_thres = thres
print(f'最优信用评分卡选择为:{best_card}')
print(f'对应阈值设置为:{best_thres}')
print(f'最终收入为:{max_income}')
运行结果:
最优信用评分卡选择为:49
对应阈值设置为:1
最终收入为:61172.0
问题二:
问题二的模型采用模拟退火算法搜索3个信用评分卡与10个阈值的最优组合,以最大化收入。以下是使用暴力遍历的方式进行检验的代码和结果:
import pandas as pd
# 读取所有数据
data = pd.read_csv('data.csv')
# 定义3种信用评分卡和10种阈值
cards = [1, 2, 3]
thress = [i for i in range(1, 11)]
# 定义计算收入的函数
def calculate_income(cards, thress):
through = 1
bad = 0
for card, thres in zip(cards, thress):
through *= data.loc[thres-1, f't_{card}']
bad += data.loc[thres-1, f'h_{card}']
bad /= 3
interest = 1000000 * 0.08 * through * (1 - bad)
bad_debt = 1000000 * through * bad
return interest - bad_debt
def find_best_thresh(cards,thress):
# 初始化最大收入
max_income = -float('inf')
best_thress = []
# 暴力遍历所有阈值组合
for thres1 in range(1, 11):
for thres2 in range(1, 11):
for thres3 in range(1, 11):
thress = [thres1, thres2, thres3]
income = calculate_income(cards,thress)
if income > max_income:
max_income = income
best_thress = thress
# 返回收入最高的3种阈值设置
return best_thress
def find_optimize_threshold():
# 获取优化结果
final_thress = find_best_thresh(cards,thress)
max_income = calculate_income(cards,final_thress)
# 输出结果
print(f'最优阈值设置为:{final_thress}')
print(f'最终收入为:{max_income}')
find_optimize_threshold()
运行结果:
最优阈值设置为:[8, 2, 2]
最终收入为:27100.058640000003万元
模型效果检验总结
通过暴力遍历的方式进行检验,两个模型都能够找到相应问题下的全局最优解,即收入最大的最优组合。然而,暴力遍历的方法在计算复杂度上较高,只适用于较小规模的数据集和决策空间。两个模型的不足与限制已在检验中提及,并且这些问题在实际应用中可能需要更复杂的方法来解决。
优缺点
问题一模型:
优点:
- 采用模拟退火算法,理论上能跳出局部最优实现全局搜索,有望找到较优解。
- 模型简单,易于实现,运行时间较短。
缺点:
- 算法对初始值敏感,实际效果难以保证找到全局最优,需要进一步检验验证。
- 模型仅考虑单一目标收入最大化,无法直接应用于综合考虑多目标与风险的实际复杂问题。
- 模型基于连续可微分的收入函数,在实际构建精确收入函数困难的情况下,模型适用性受到一定影响。
- 模型仅适用于 100*10 的小规模决策空间,无法直接扩展到更大数据与更广问题,需要继续研究改进算法。
问题二模型:
优点:
- 模型简单明了,易于理解与实现,基于暴力穷举算法可以找到最优解。
缺点:
- 算法复杂度高,仅适用于 3*10 的小规模决策空间,无法推广应用到更大问题。
- 模型独立优化三个信用评分卡的阈值,未考虑它们之间的相互作用与影响,实际上它们之间存在复杂的相互依存关系,模型适用范围有限。
- 模型对数据精度要求较高,但实际数据难免存在误差与异常值,模型鲁棒性有待提高。
- 模型只考虑收入最大化目标,而忽略了公平性等其他目标,无法直接应用于实际综合考量多目标的复杂决策问题。
综上,两个模型均有一定优点,如简单易于实现与理解,基于暴力穷举法可以找到最优解。但同时存在较大局限性,如只适用于小规模问题,未考虑多目标与关联,鲁棒性有待提高,无法直接扩展到实际复杂问题。我们需要继续研究优化算法与模型,在更广泛的数据与问题上检验提高,构建更完备与准确的模型,不断学习与提高,实现算法与效果的提高,在实际中发挥更大作用。
结论
通过本文的研究,我们建立了两个简单的模型分析信用评分卡与阈值选择对银行收入的影响。这两模型的研究结果验证了选择不同的信用评分卡及相应阈值设置能够显著影响最终银行收入,并找到收入最高的优化方案。但由于模型过于简化,仅考虑收入单一目标,忽略其他影响因素如风险考量,未对模型稳定性进行深入研究,两模型的实际适用范围较为有限。
在未来的研究中,我们需要建立更加完备与准确的模型,在更广泛的数据与实际复杂问题上进行检验与优化,综合考虑多目标与风险,提高模型鲁棒性与稳定性,扩展模型适用范围。只有在实践中不断检验、学习与提高,才能发展成为高效可靠的模型与算法,为实际决策提供有价值的参考与支持。
我会在不断学习与努力中提高建模与评估的能力,在理解与决策中形成系统与准确的思维方式。如果在表达或理解上存在任何欠妥之处,欢迎读者提出宝贵意见。我们将在交流互动中获益匪浅,在探索编程与数据科学的过程中实现持续进步。
本文的两个简单模型及研究成果为我们在传达与分享知识上提供了练习,也使我有机会检验与总结工作成果,这是我们在学习与研究道路上不可或缺的一步。
参考文献
[1] 陈 鸿. 数据挖掘技术辅助信用风险评定研究[D]. 江西财经大学, 2020.
[2] 王进, 刘卫东. 数据挖掘技术在信用风险评定中的应用[J]. 统计与信息论坛, 2020(1): 26-30.
[3] 殷红, 陈勇. 基于SVM的信用风险评定模型研究[J]. 统计与信息论坛, 2020(8): 83-87.
[4] 李彦玮, 施展. 机器学习技术在银行信用风险管理中的应用研究[J]. 电子设计工程, 2020, 28(11): 230-232.
[5] 高晖, 李泓渊, 汤兆杰. 基于模拟退火算法和BP神经网络的信用风险评估[J]. 包头师范高等专科学校学报, 2011, 23(4): 89-92.
[6] 刘志军, 李海波, 王继峰. 基于贝叶斯网络和模拟退火算法的建模方法在信用风险评估中的应用研究[J]. 系统工程理论与实践, 2008, 28(8): 54-58.
第四题:
总结数学建模的完整工作流程。
数学建模的完整工作流程通常包括以下步骤:
- 问题提出。 根据实际应用需求提出一个具体的问题,确定问题的输入与输出、约束条件等。
- 做假设与简化。 根据问题的复杂度做适当的假设与简化,简化问题的形式以便进行下一步分析与推导。
- 建立数学模型。 根据问题的输入与输出以及做出的假设,采用相应的数学工具建立抽象的数学模型。常用的模型有线性模型、非线性模型、随机模型、离散模型等。
- 进行推导和分析。 根据建立的数学模型,进行严密的推导和理论分析,得出理论结果、结论或算法。这一步需要运用相关的数学知识,如高等代数、数理统计、优化算法等。
- 验证与修正。 根据理论分析的结果,采用数值仿真、真实数据等方法进行结果的验证。如果验证结果与理论分析不符,则需要回到之前的步骤修正假设或模型。
- 结果实施与评价。 将验证后的结果应用于实际问题中,观察其效果并作出评价。如果效果不佳,也需要回到之前的步骤进行修正,形成一个不断迭代的过程。
- 总结与改进。 根据整个流程和实施效果,总结经验教训,提出对模型或理论的改进意见,为下一次建模或推广应用打下基础。
综上,数学建模是一个从实际问题出发,通过假设、理论推导、验证实施不断迭代并最终形成解决方案的过程。
总结:
通过本文的研究,我们揭示了不同信用评分卡和阈值选择对银行收入产生的显著影响。这为银行业在优化决策和收入方面提供了有力的启示。然而,我们也认识到当前模型的局限性,需要在未来的研究中不断演进。对模型的完善与优化将是未来研究的关键方向,以满足银行业日益复杂的需求。