FOC学习记录——原理篇

0 说明

此文章是为了记录学习FOC的过程，包括FOC原理及软硬件实现等内容。看了很多大佬的文章，写的不错，但是有些用词还是没让我觉得通俗易懂，所以自己想来写一个自己方便理解的，写的能让别人看懂了，说明我自己也就学会了。
在学习过程中参考了很多大佬的文章等内容，会加以标注的。如果各位客观发现文中有错误，还望指正。理性探讨。

参考资料：
https://blog.csdn.net/jdhfusk/article/details/120395938 （有些图不错）
https://zhuanlan.zhihu.com/p/147659820 （大佬文章，内容很干很长）
https://blog.csdn.net/weixin_43229030/article/details/115407480 （用了一张图）
https://zhuanlan.zhihu.com/p/56529497 （解释一个数字的问题，还是没看懂。。。）

1. 无刷电机

这里不介绍无刷电机与有刷电机的区别，直接说无刷电机。

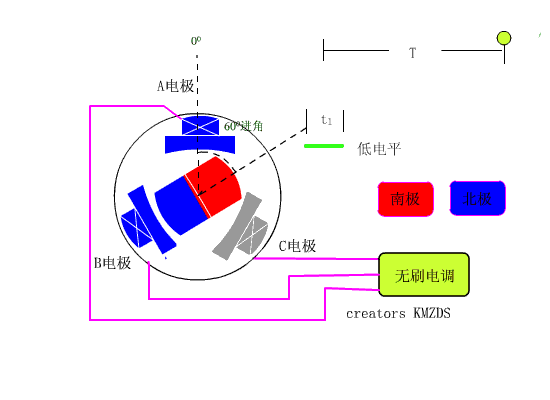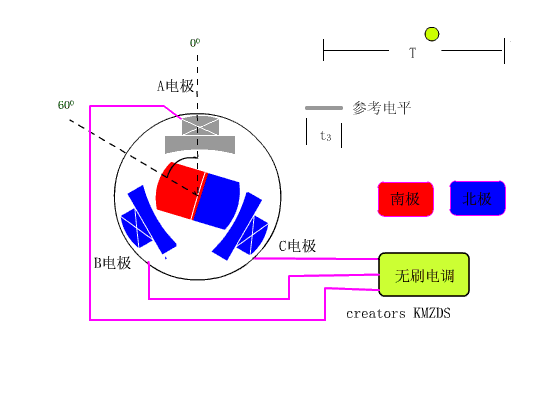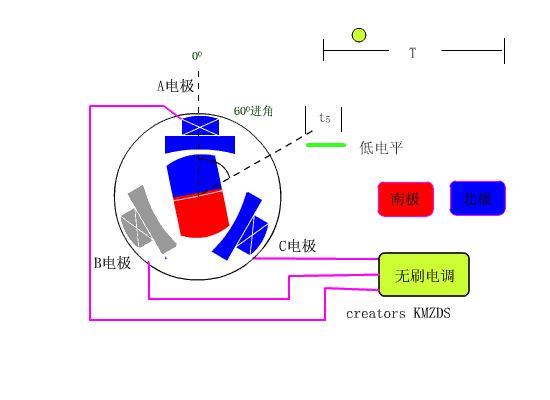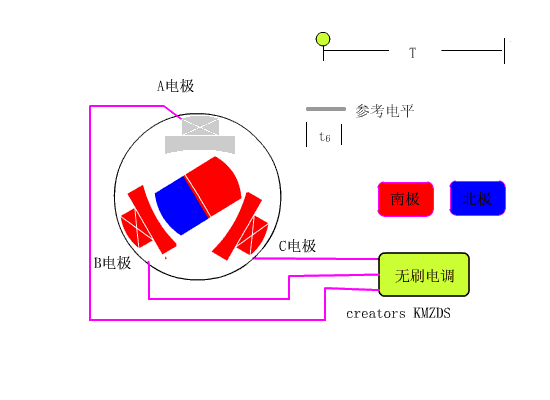
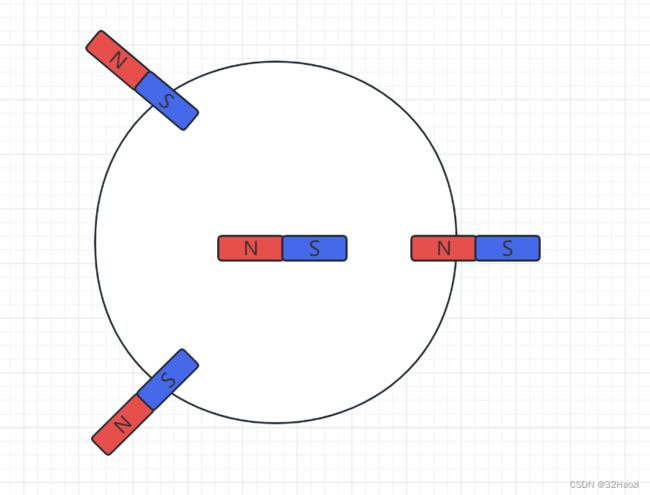
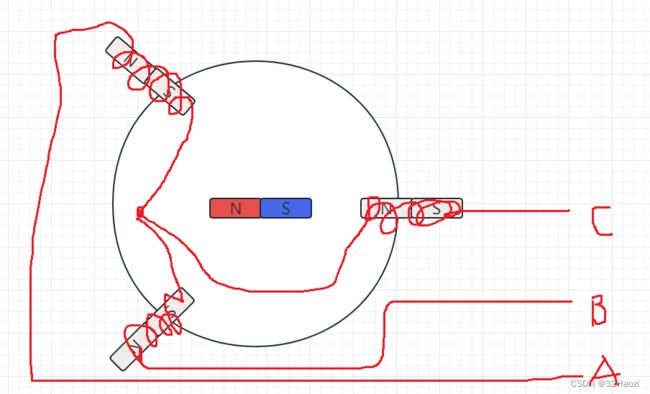
无刷电机外露的有三条线，分别对应到电机定子的三个线圈（实际上，大多数电机都不止有三个线圈）。

中间的转子可以视作是一个磁铁（实际上比这个略微麻烦点，说算法的时候说）。而定子是三个线圈，线圈上面缠绕了三个电机线，以星形连接，在外面引出。当有电流通过线圈时，线圈也就可以看作是磁铁了。

2. 六步换向法

最简单的转子转动的方法如下图所示。

第一步：假如某时刻，电机转子位置，如左图所示。电流从A相流入，B相流出（记作：电流AB），则如左图所示，线圈被等效为两个磁铁。此时，转子收到两个线圈的合力，会逆时针旋转至右图的位置，然后停止。

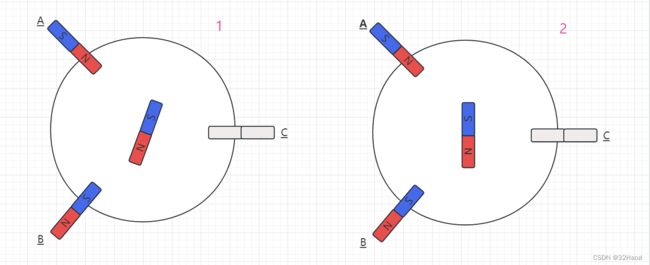
第二步：此时，转换电流，把电流改为从A相流入，C相流出（记作：电流AC），此时，转子收到两个线圈的合力，会逆时针旋转60°至右图的位置，然后停止。

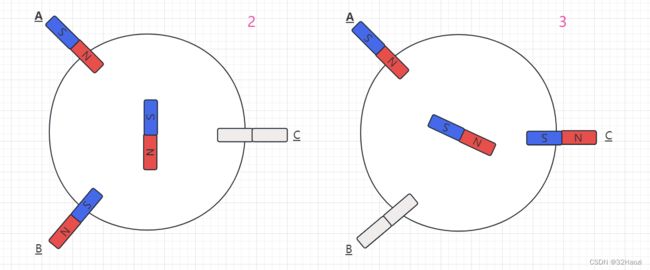
第三步：此时，转换电流，把电流改为从B相流入，C相流出（记作：电流BC），此时，转子收到两个线圈的合力，会逆时针旋转60°至右图的位置，然后停止。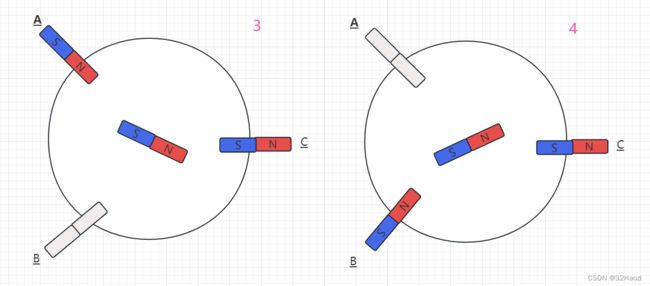
第四步：此时，转换电流，把电流改为从B相流入，A相流出（记作：电流BA），此时，转子收到两个线圈的合力，会逆时针旋转60°至右图的位置，然后停止。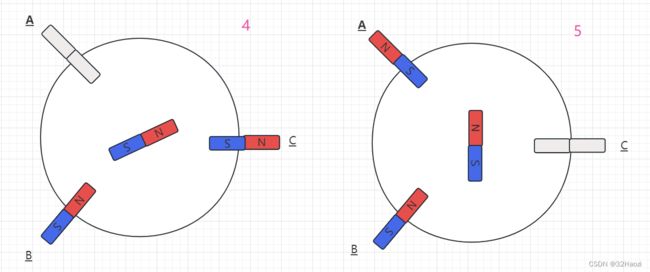
第五步：此时，转换电流，把电流改为从C相流入，A相流出（记作：电流CA），此时，转子收到两个线圈的合力，会逆时针旋转60°至右图的位置，然后停止。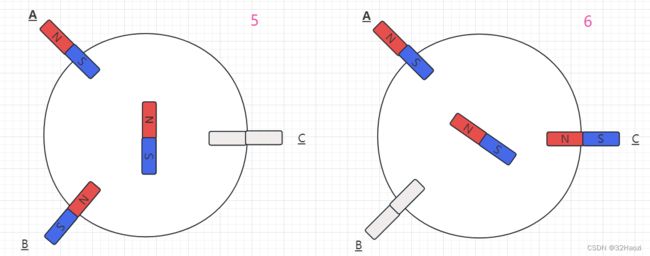
第六步：此时，转换电流，把电流改为从C相流入，B相流出（记作：电流CB），此时，转子收到两个线圈的合力，会逆时针旋转60°至右图的位置，然后停止。
此时，又回到了初始的位置。

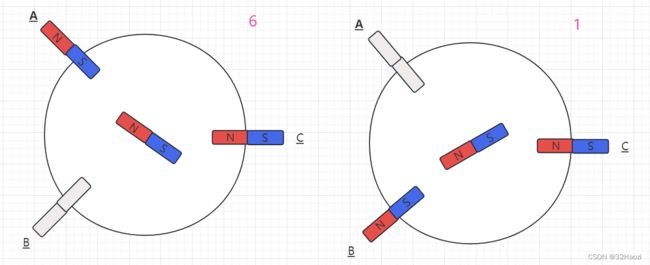
经过上述步骤可以发现，如果想让电机逆时针转动，只需要按照顺序不断调整电流方向就可以了。

逆时针转动：AB => AC => BC => BA => CA => CB => AB

顺时针转动：AB => CB => CA => BA => BC => AC => AB

这就是最简单的六步换向法。

每次换向可以使得转子转动60°，通过六次换向使得转子转动一周。
不断循环，便可以使得转子不断转动。

3. 驱动电路设计

电机内部采用星形连接，每次更换两条通电的电路（第三条线暂且悬空不用管），可以产生一定的磁场，吸引转子达到一个固定的角度后停下来。图中画的转子的位置就是不会再发生转动了的位置。可以看出，定子刚好逆时针转了一圈。循环往复就能让转子不停的转动了。这个电压方向不断变化的动作就是换相。这个换相动作就是由控制器完成的，控制器按照一定的频率换相，就能控制电机的转动了。

注意：转速与换相频率无关！！！无关！！！无关！！！ 换相是个被动的动作，当达到一定的角度是需要你进行换相。而不是你随意换相了他就能达到某一个角度。越大的电压能让电机转子转的更快，转得越快就需要越快的换相频率。

从上面的分析我们可以看出来，对于电机三相的每根线来说，电流都有两种情况：流入和流出。如下图所示。

而我们常用的直流电源是无法做到这一点的。因此我们需要一个电路，对电流进行转换。

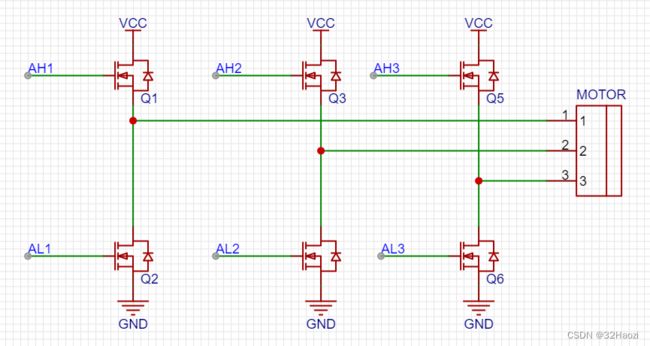
如下图所示，当AH1为高电平、AL1为地点平时，上侧MOS打开、下侧MOS管断开，电流从上往下流，然后流入电机。
而AH3为低电平、AL3为高点平时，上侧MOS断开、下侧MOS管打开，电流从上往下流，从电机中流出，最后流到电源负极。

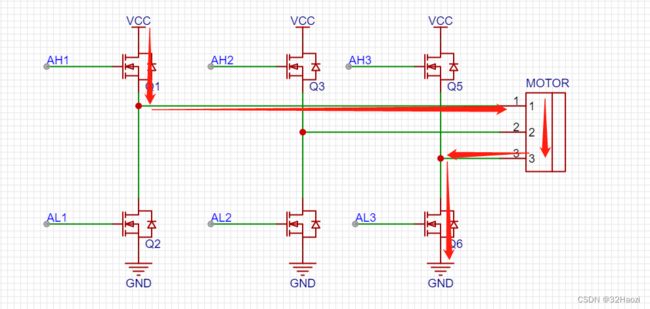
在上图中，第二相是没有用到的，但是实际上，这也是可以同时用到的。而且并不影响上面六步换向法的分析结果。

然后分析一下，电路的导通情况。
假设：

• 上桥臂导通、下桥臂断开 记为：1
• 上桥臂断开、下桥臂导通 记为：0

那么一共有八种情况。分别为：000、001、010、011、100、101、110、111.

注意，01不可能同时存在，即某一个相不可能上下桥臂都打开，否则，这电源不是被短路了吗？
如果上下桥臂都断开，那就不起作用了，多一个有什么不好的呢。

4. 电动机与发电机

为了明白如何控制发动机，我们先复习一下发电机。

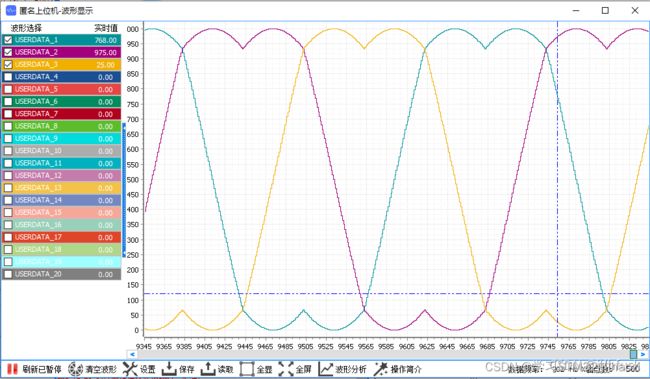
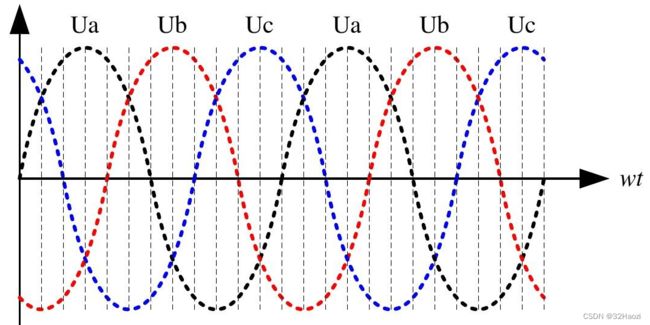
对于三项交流发电机，使其匀速转动之后，其产生的三项电电压变化如下图所示。

具体到我们生活中，发电机的电压曲线也是这样的，峰值为380V，有效值为 380V / 1.732 = 220V.

那么，这里的发电机 跟 电动机 有什么区别吗？

答：原理上没有什么区别。只不过一个是你拉着它转，他给你电。另一个是你给他电，它拉着你转。

因此，得出结论，我们给电机这样的三项交流电，那电机就能匀速转动了。

反电动势：电机和发电机其实可以认为是同一个东西。当电机通电旋转的时候，它实际上是一边被磁场力拖着转动，同时也因为它在转动而在发电。发的这个电就是反电动势。理想空载的情况下，电机发电的电压和加在电机线圈上的电压是相等的，也就是说加在电机上的电压恰好被反电动势给抵消了。

5. 沙雕控制方法

以上面的结果为分析情况，先以电机匀速转动为目标，来做个案例看看。

如果想让电机匀速转动，只需要控制电机三相上的电流按照图上标注的大小转动就可以了。其中θ是转子的实时角度。

因此，我们就可以获得如下的控制框图。

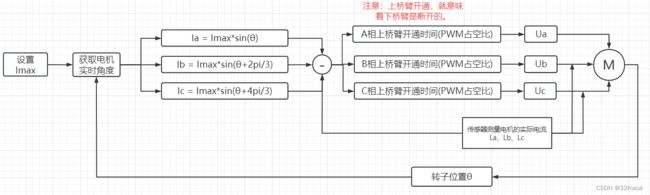
设定的三个相的电流 是需要随时根据转子的角度进行调整的，然后和实际的电流进行对比，根据对比结果调整占空比的大小，进而控制电压大小，最后实现控制电流大小的目的。

而电机转动的速度是由Imax决定的，因为电流越大 => 线圈产生的磁场越强 => 对转子的拉力越大 => 转动的越快。

而转的越快，也就需要更快的电流更新速度。

因此，我们发现，其实上图就是电机控制的力矩环，而速度环，可以通过计算需求速度与实际速度的差值，并将这个差值设置为Imax即可。

需要明确的是，真正控制电机力矩的是电流，而我们控制电流的方法是 控制电压大小来调整电流。
另外，上图中省略了PID的部分，实际上电流反馈做差之后，是需要利用PID进行调整的。这里只是个表示，不影响分析。

根据上述控制过程可以发现，在这个过程中我们需要控制三个量，而且是不断变化的，及其不方便，因此，我们需要一种简单的控制方法。

6. FOC控制

接下来就是我们的正题：FOC控制。
简单来说，我们的目的就是：避免直接控制上面提到的三个量，尽可能的对其进行简化。

以下PID算法默认都会。

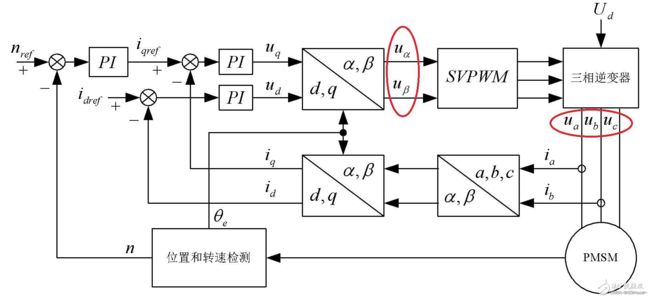
先放个FOC控制的流程图，然后慢慢解释：

上图中的控制流程为：

1. 计算电机三条电机线上的电流：Ia、Ib、Ic
2. 对电流Ia、Ib、Ic进行Clark变换得到Iα、Iβ
3. 对Iα、Iβ进行Park变换得到Iq、Id
4. 将Iq、Id与设定的Iq_ref、Id_ref计算误差
5. 将计算的误差用PID控制器(上图中只有PI控制)计算控制电压Uq、Ud
6. 对Uq、Ud进行反Park变换得到Uα、Uβ
7. 用Uα、Uβ合成空间矢量，输入SVPWM输出编码值（前文说的8种情况）
8. 按照编码值赋值给MOS管驱动电机
9. 循环重复以上步骤

然后解释以下上述流程：

在解释开始之前，一定要牢记一点：下面说的电流矢量或者电压矢量就可以直接理解为力矩矢量，这之间只需要单位变换，其实都是一样的。

6.1 电流检测

我们上面电动机和发电机的沙雕控制案例说明，我们需要控制电机三个相的电流，使得三个相的电流和矢量沿着我们预期的方向。如图，将Ia、Ib、Ic作为基向量，我们控制其大小，就可以调整磁场合力的方向和大小，实现控制转子旋转的目的。

因此，我们需要对实际电路中三个相上的电流进行检测，以便于进行反馈控制。

实际上，上图中我们只检测了两个相上的电流。因为根据基尔霍夫电流定律，电流之和等于0，可以轻松求得第三相的电流。在硬件上还可以少一个检测部分的成本。

6.2 Clark变换

在得到检测的电流Ia + Ib + Ic之后，我们知道电流I = Ia + Ib + Ic。

存在两个问题：

1. 而我们上面的分析得知，Ia、Ib、Ic三个量是需要根据角度而变化的，如果直接进行反馈（就是上面沙雕控制算法的意思），这个量还是需要算的，而我们不想控制这种一直变换的量。
2. 我们知道了Ia、Ib、Ic，但仍然不好说清楚和矢量到底指向哪个方向，因为这三个向量不是正交的。而我们习惯上使用两个垂直的量作为基向量进行描述。

为此，我们可以使用Clark变换进行解决。

克拉克变换（Clark）基本形式如下：
$$\begin{gathered} I_{\alpha }=I_a-\cos (\frac{2\Pi }{3})I_b-\cos (\frac{2\Pi }{3})I_c \\ {I}_{\beta }=\sin (\frac{2\Pi }{3})I_b-\sin (\frac{2\Pi }{3})I_c \end{gathered}$$

写成矩阵形式如下（这带的公式编辑器真难用）：

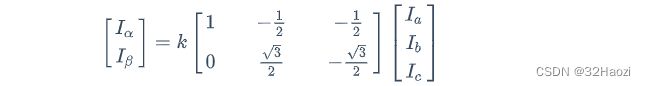
注意，此处增加了一个系数k，在此基础上，为了后面好写，把这个系数矩阵记为C(Clark)，我们就可以有如下变换：

I = [Iα、Iβ].T = k*C*[Ia、Ib、Ic].T

这样只要带入我们测得的Ia、Ib、Ic，我们就可以用Iα、Iβ来表示了。如下图所示。

然后来解释一下上面的那个k，公式中的k一般有三种取值，分别为k=1、k=2/3、k=根号下三分之二。分别表示Clark变换的基本形式、等幅值形式、等功率形式。

这里主要解释前两个。

我们任意带入一个数进去转换一下试试看，比如Ia=-1、Ib=1/2、Ic=1/2（即电流从A相流入，BC相流出）

这三个量表示的是电流，任意带进去的数一定要满足基尔霍夫电流定律，即Ia + Ib + Ic矢量和等于0。

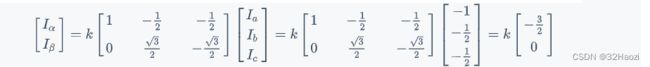
可以看到，结果中，当k=1时，Iα和原始的Ia并不相等，相差了2/3倍。
再结合Ia + Ib + Ic = 0，可以简化我们的Clark变化结果。
$$\begin{gathered} I_{\alpha }=\frac{3}{2}{I}_a \\ {I}_{\beta }=\frac{\sqrt{3}}{2}(2I_b+I_a) \end{gathered}$$

而Clark变换的等幅值形式，即当k=2/3时，带入上述公式：

$$\begin{gathered} I_{\alpha }=I_a \\ {I}_{\beta }=\frac{1}{\sqrt{3}}(2I_b+I_a) \end{gathered}$$

可以发现，Iα=Ia可以一直成立，更加简化了我们的变化结果。

可以看出，我们只需要两路电流就可以计算了，这也是为什么最上面的电路图中只有两路电流检测了。

这样我么就减少了一个被控制的量，而且方便描述了。但是如果按照Ia、Ib、Ic的正弦波变化规律，并把它带入到Iα、Iβ中可以发现，其实Iα、Iβ还是两个一直变化的量，还是正弦波。

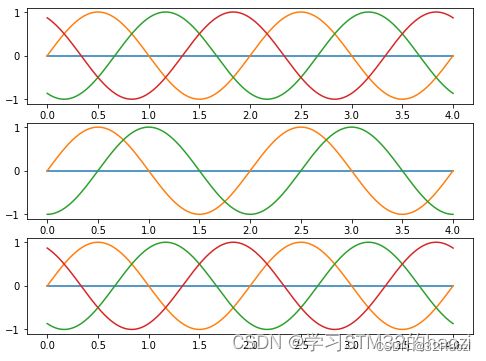
如下图所示。从上到下，是原始数据、Clark变换后的数据、再反变化的数据。可以看出，经过变换后的数其实还是正弦波。也就是第一个问题仍然存在。

6.3 Park变换

在经过上面的变换后，假设某时刻，转子的位置与α轴（x轴）的夹角为θ。

转子受到的力可以分解为两个方向，一个是沿着转子旋转切线方向的Iq向量、另一个是沿着半径向外的Id分量。

显然，Id分量对于电机的旋转是没有什么作用的，因此实际上我们也不期望他有值，恒等于0是最好的了。

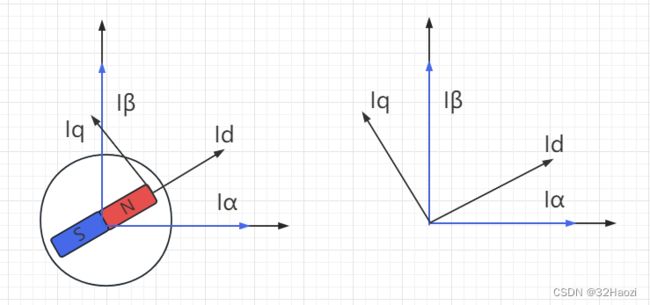
那怎么样用Iα、Iβ来表示我们期望的Iq、Id呢，那就是Park变换。
我们把坐标轴旋转θ度。帕克（Park）变换公式如下：

$$\begin{gathered} I_d=\cos (\theta )I_{\alpha }-\sin (\theta ))I_{\beta } \\ {I}_q=-\sin (\theta )I_{\alpha }+\cos (\theta )I_{\beta } \end{gathered}$$

写成矩阵形式如下：

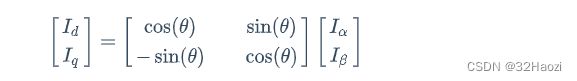
在此基础上，为了后面好写，把这个系数矩阵记为P(Park)，我们就可以有如下变换：

I = [Iq、Id].T = P*[Iα、Iβ].T = P*C*[Ia、Ib、Ic].T

即：

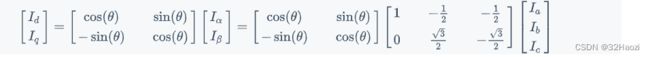
此时，如果将Ia、Ib、Ic最开始分析的正弦波带入上面的公式，就会发现，Iq、Id其实是两个常量。

Iq=1、Id=0

---

得到上面这个结论，其实就已经理解了大部分的FOC算法了。

因为，我们发现，把三个正弦波经过两次这样的变换就能得到两个常量，那我们设定两个这样的常量，在赋值给电机电压时，根据电机转子的角度，逆向变换过去，这样不就只需要控制两个常量了吗。

这也就是上面的控制步骤中，第4、5、6步的做法。

4. 将Iq、Id与设定的Iq_ref、Id_ref计算误差
5. 将计算的误差用PID控制器(上图中只有PI控制)计算控制电压Uq、Ud
6. 对Uq、Ud进行反Park变换得到Uα、Uβ

注意，经过PID计算后，原有的电流向量变成了电压向量，因为电流是通过电压控制的，我们直接控制不了电流。
PID默认都会。

6.4 SVPWM

上面经过分析：把检测到的电机电流经过一系列变换，得到向量q、d的大小，并且和设定的q=1、d=0比较，然后在经过反变换得到三相应该赋予的电压就可以控制电机转动了。

但是实际上在上面写的步骤中，只用到了反Park变化，而没有反Clark变换，在进行反Park变化之后直接使用了SVPWM模块。因此，来分析一下SVPWM的过程和目的。

空间电压矢量分析

我们需要再次看一下我们电路小节的分析，已经说过，电路根据MOS管的开断，一共有八种合法状态。

分别来看一下这八种状态可以产生的电压矢量方向。

比如状态（1，0，0），MOS管开断情况如下图。

此时，电机三个线圈的磁方向如下图左图所示，而根据电路分压定律，电机三个相的相电压分别为下图右图所示。

如果规定从电机三相中性点向外的向量为正。则Ua为正，Ub为负，Uc为负。则电压和矢量的方向为正、模为VCC。如下图中间图所示。

如果我们把八种情况都画出来，驱动电路可以产生的八种电压向量如下图所示（其中000，111两种的和矢量模为0，就是原点的一个点）。得出结论，我们可以产生七种不同方向的力矩（包含0矢量），并且这几个矢量把360度划分为了6份，称之为扇区，分别标号为1-6。

U1-U6的名字是按照对应数字的二进制编码起的。

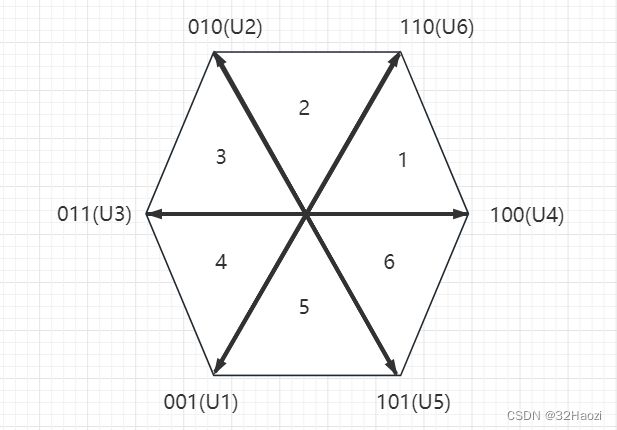
接下来要做的，是反Park变换得到Uα、Uβ之后，如何用上述的七个矢量产生任意需要的和矢量。

举个栗子：

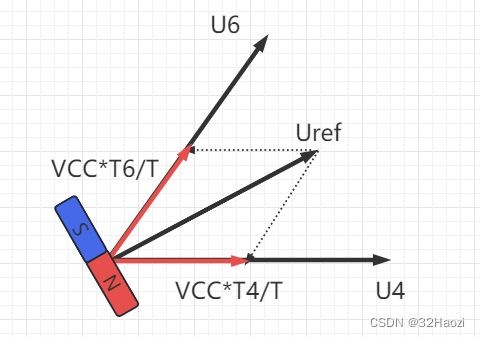
假设某个时刻，我们需要的电压和矢量角度为θ（0 < θ < 60），Uref为期望的电压和矢量。如下图所示。

想一下：此时转子的角度为多少？
答案：θ-90度。因为我们期望的力矩和，一直是沿着转子旋转的切线方向的。

如果我们需要产生Uref，我们只需要调整U6和U4的大小就可以了。

而U6和U4的大小可以通过调节MOS管的开断时间决定。图中，T表示周期长度，T4、T6表示U4、U6的持续时间长度。

显然，T4 + T6 小于等于 1

先明确一点：这里只说U4和U6，他们的最大值Umax为多少？这里按照 2*VCC/3计算。至于为什么不是VCC，等我搞明白了再来写。确定的是不影响下面的分析过程。

比如：MOS管的开断一直在U4和U6之间等时间切换，则U4 = U6 = Umax/2 = VCC/3，则Uref = 根号三VCC/3。

那么对于任意的Uref，只需要根据其角度和模，计算T4和T6的时间就可以了。
计算过程如下，根据正弦定理：

$$\frac{|U_{ref}|}{sin(\frac{2\pi }{3})}=\frac{|\frac{T_6}{T}{U}_6|}{sin(\theta )}=\frac{|\frac{T_4}{T}{U}_4|}{sin(\frac{\pi }{3}-\theta )}$$

把U4 = U6 = 2*VCC/3带入，得：
$$\begin{gathered} T_4=\sqrt{3}\frac{|U_{ref}|}{VCC}T\sin (\frac{\pi }{3}-\theta ) \\ {T}_6=\sqrt{3}\frac{|U_{ref}|}{VCC}T\sin (\theta ) \end{gathered}$$

剩下的只需要带入Uref的角度和模即可。

如果T4 + T6 < T，则剩下的时间均分给零向量（U0、U7），即T0 = T7 = (T - T4 - T6)/2。

至此，就说明白了怎么在某个扇区内产生任意大小和方向的电压向量，当Uref在其他扇区内也是一样的方法。

6.5 MOS管开断顺序

我们求得了T4、T6、T0、T7的时间，接下来，要把上述时间分配给MOS管，控制MOS管的开断。控制逻辑方式如下图：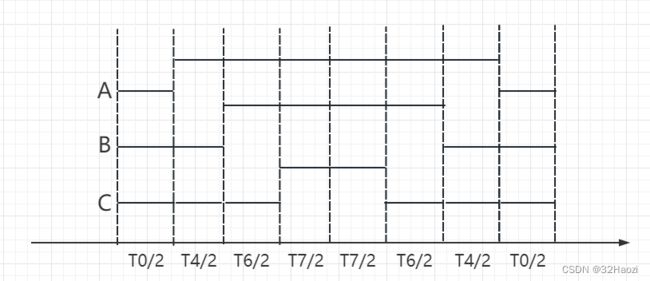
可以看出，MOS管的开断顺序为：000->100->110->111–>111->110->100->000。只需要控制MOS管按照这个顺序开断，并且每次开断的时间控制好，就可以产生需要的电压矢量了。

上述切换顺序，可以减少MOS管开断的次数，每次切换只有一组MOS管切换状态。

同理，我们将其他五个扇区也用同样的方式写出来。

则不同扇区的切换顺序分别为：

期望向量所在的扇区	MOS管切换顺序
1（0-60）	0-4-6-7-7-6-4-0
2（60-120）	0-2-6-7-7-6-2-0
3（120-180）	0-2-3-7-7-3-2-0
4（180-240）	0-1-3-7-7-3-1-0
5（240-300）	0-1-5-7-7-5-1-0
6（300-360）	0-4-5-7-7-5-4-0

最后一步，这个MOS管的切换顺序和持续时间都有了，使用硬件控制就可以了。

至此，我们就搞完了电机最内环（电流环/力矩环）的控制流程。

7. 完整控制流程

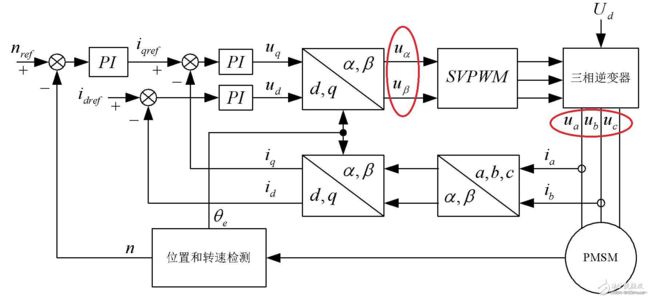
上图中除去nref之后，就是电机控制最内环的FOC控制算法了，流程已经讲完了。

总结一下：
上图中，设定iq=1、id=0，然后按照上述控制流程，就可以使电机按照三个项的电流按照正弦波的波形变化了（仔细思考一下，这里的正弦波是把电机中性点看作地而量出来的）。

然后来扩充：
如何实现速度和位置控制呢？看下图（来自大佬的图片，看水印）。
这个应该是很清晰了，就不过多介绍了。

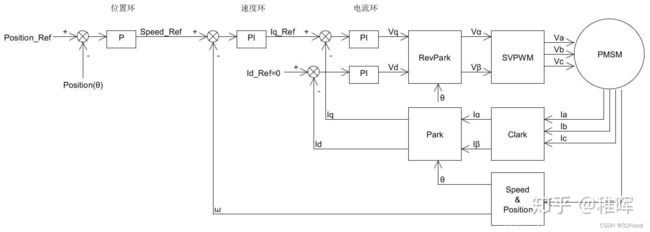
好了，你已经学会FOC算法了，接下来来造个火箭吧。

8. 硬件篇 和 软件篇

开源链接：https://gitee.com/HzoZi/foc

9. 补充概念

9.1 BLDC、PMSM

无刷电机可以分为无刷直流电机（BLDC）和永磁同步电机（PMSM），结构大同小异，主要区别在于制造方式（线圈绕组方式）不同导致的一些特性差异（比如反电动势的波形）。

第一种，我们分析可以看出来，转子一共有六个平衡状态（看六步换向法），在每次换相的时候力的大小和方向会发生改变，因此会有扭矩的抖动。但是如果我们把磁极多增加几对，转子就会有更多的平衡状态，这样同样的旋转角度，抖动的次数变多了，但是抖动的程度就可以小的很多很多了。这就是**无刷直流电机（BLDC）**的解决方式，可以看文章刚开始的图，有很多对线圈。

第二种，也就是永磁同步电机（PMSM） 的解决方法。BLDC的反电动势被设计成了方形波，不管哪条线电压都是只有 有或者没有两种状态。而PMSM被设计成了正弦波。我们可以使用软硬件的手段将方波转变成等效的SPWM正弦波或者SVPWM马鞍波就可以完美的驱动电机运行了。这就是FOC。FOC（Field-Oriented Control），直译是磁场定向控制，也被称作矢量控制（VC，Vector Control），可以实现磁场方面的像素级控制。

9.2 马鞍波

我们一直说，驱动电机运转使用的是正弦波。
但是这个正弦波是把电机中性点看作是0电势点来说的。

但实际上，我们一般认为的 0电势点 是 GND。也就是电源负极。
而在这种视角来看，测量电机三相的电压就会发现，其是一个马鞍波，如下图所示。