建立二叉树:已知层次遍历顺序建立二叉树、已知先序遍历顺序建立二叉树
其他二叉树知识!二叉树知识汇总
目录
前提知识:
约定:
二叉树节点的存储结构:
创建一个节点:
建立二叉树的几种方法:
一、已知先序遍历顺序,构建二叉树。(链式存储)
二、已知层次遍历顺序,构建二叉树。(链式存储)
三、已知节点关系,建立二叉树(邻接表存储)
四、已知先序和中序遍历顺序,建立二叉树。
前提知识:
约定:
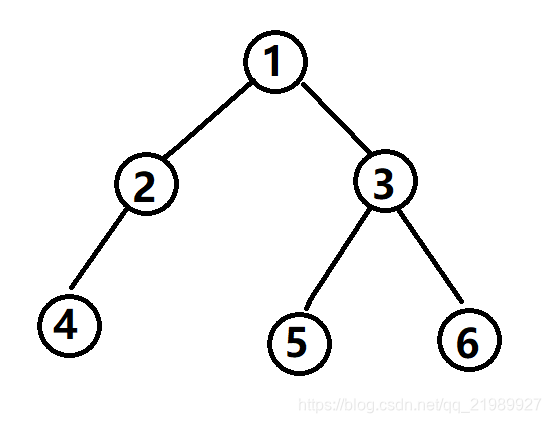
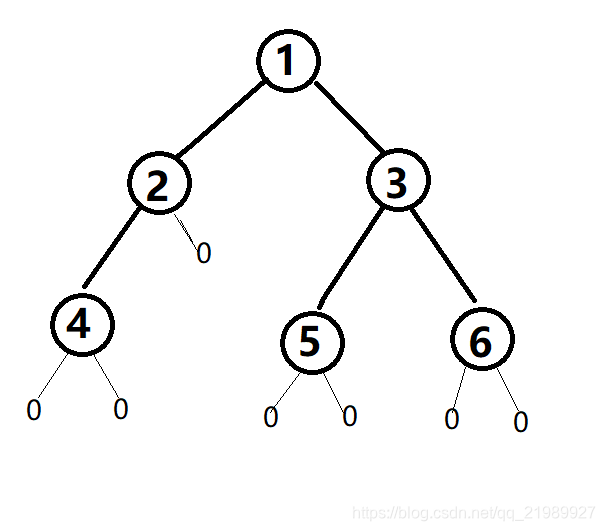
约定二叉树的内容为int类型,并且都>=1,0代表是空节点。我们一般画的二叉树为图一,但是计算机中存储时真实的样子是图二,即需要考虑空节点,不然的话,计算机不知道这个节点已经到头了。
例子中树的先序遍历为:1 2 4 3 5 6
若是考虑每个节点的两个空节点,则先序遍历为:1 2 4 0 0 0 3 5 0 0 6 0 0
二叉树节点的存储结构:
struct Node{
int data;
Node* leftchild;
Node* rightchild;
};一个存储数据的data,左右两个指针都是节点的指针类型。
创建一个节点:
void Create_Node(Node* &t,int x){ //在指针t处生成一个新的节点,内容为x
t=new Node;
t->data=x;
t->leftchild=NULL;
t->rightchild=NULL;
}开辟一个新的Node类型空间,并将地址赋值给指针t。(原来t指向NULL,现在指向了我们生成的新节点,这就是创建节点的过程)
另外新节点*t的左右孩子要指向NULL,这代表节点到此结束,不赋初值会导致一些错误。
参数的问题:
Node * &t 这个参数表示传入的是一个Node类型的指针变量,并且是引用传递,因为我们要修改实参的值,所以要用引用传递。
不懂引用的看这里:https://blog.csdn.net/qq_21989927/article/details/107447970
建立二叉树的几种方法:
一、已知先序遍历顺序,构建二叉树。(链式存储)
这里的先序遍历顺序,必须是包含空节点的,不然是无法确定二叉树的。
样图中的数的先序遍历顺序:1 2 4 0 0 0 3 5 0 0 6 0 0
void Create_Pre(Node* &t){
int x;
cin>>x;
if (x==0) return;
else{
Create_Node(t,x);
Create_Pre(t->leftchild);
Create_Pre(t->rightchild);
}
}
对于输入的x,若是0,说明是空节点,直接返回return。
若不是空节点,则调用前提知识中的Create_Node函数,在此处创建一个新节点,接着再递归新节点的左右孩子。
因为已知的是先序遍历顺序,所以我们是按先访问根,再访问左右孩子的顺序。
二、已知层次遍历顺序,构建二叉树。(链式存储)
这里又分两种方法:一种是边读入数据边建立二叉树,需要用到队列;另一种是已知的层次遍历顺序在数组中存放好了。
1.使用队列
这种方法样例对应的读入是:1 2 3 4 0 5 6 0 0 0 0 0 0 (0是空节点)
void Create_Level(Node* &t){
queue q;
int x;
cin>>x;
if (x!=0) {
Create_Node(t,x);
q.push(t);
}
while (!q.empty()){
Node* s=q.front();
cin>>x;
if (x!=0){
Create_Node(s->leftchild,x);
q.push(s->leftchild);
}
cin>>x;
if (x!=0){
Create_Node(s->rightchild,x);
q.push(s->rightchild);
}
q.pop();
}
} 使用队列的方法,首先要入读一个x,判断这棵树是否存在,若是0,说明空树,不为0,创建节点后入队。
当队列不为空时,队列中每一个元素都需要再读取两个数字(就算是叶子节点也起码也得读两个0)。
这种方法建立二叉树,执行过程中会发现,每次读取的两个数,对应的都是队首元素的左右孩子,这和给定的层次遍历顺序对应。
2.使用数组
给定的层次遍历已经存放在数组中,我们只需要判断一个节点的左右孩子是否存在即可,左孩子为i*2,右孩子为i*2+1。
注意要从a[1]开始存储,a[0]不用。
int a[100]={0,1,2,3,4,0,5,6};
void Create_Tree(Node* &t,int i){
if (a[i]==0) return;
Create_Node(t,a[i]);
if (a[i*2]!=0) Create_Tree(t->leftchild,i*2);
if (a[i*2+1]!=0) Create_Tree(t->rightchild,i*2+1);
}
3.两种方法的区别:
建造过程的不同:
利用队列,树是一层一层被构造出来的,对数据的访问也是严格按照层次遍历的顺序执行的;
利用数组,树的构造过程实际上是先根,再左孩子,再右孩子的。通过跳跃访问数组内容,实现的是先序遍历建立二叉树。
输入数据的不同:
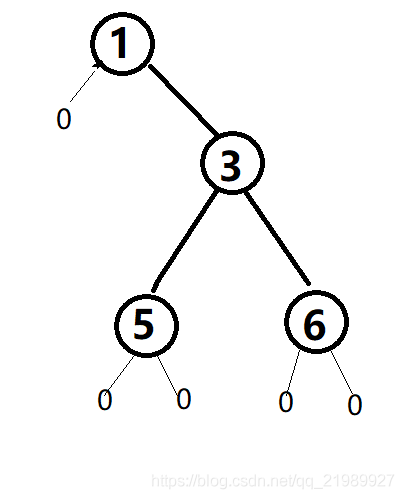
如果一棵树如图:
对于队列的方法, 输入为 1 0 3 5 6 0 0 0 0
对于数组的方法,数组中:1 0 3 0 0 5 6 0 0 0 0
因为对于队列来,如果一个节点为空节点,那么自然不会加入队列,也不会再去访问他。
而对于数组来说,要严格执行左孩子是*2,右孩子是*2+1的规则,所以空间浪费会很多。
三、已知节点关系,建立二叉树(邻接表存储)
假设题目输入中,我们只知道 x , y 之间有一条边,但是并不知道 x , y 的父子关系的时候,可以使用邻接表的方法存储树。
这时候把树看做一个图,建边要建双向边,然后在从根做dfs,确定每个节点的深度,顺便也可以求出每个节点的父亲节点,这样节点之间的父子关系就清楚了。
例题:
第一行输入N、root,表示这棵树有N个节点,根为root。
接下来 N-1 行每行包含两个正整数 x, y,表示 x 结点和 y 结点之间有一条直接连接的边(数据保证可以构成树)。求每个节点的深度和每个节点的父亲节点。
代码:
#include
using namespace std;
const int MaxN=500050;
struct Edge{
int v;
int next;
};
Edge e[MaxN];
int last[MaxN];
int n,m,root,tot;
int deep[MaxN];
int f[MaxN];
void build(int x,int y){
tot++;
e[tot].v=y;
e[tot].next=last[x];
last[x]=tot;
}
//编号为x的节点,父亲是fa
void dfs(int x,int fa){
f[x]=fa;
deep[x]=deep[fa]+1;
for (int j=last[x]; j!=0; j=e[j].next){
int y=e[j].v;
if (y!=fa) dfs(y,x);
}
}
int main(){
cin>>n>>root;
for (int i=1; i<=n-1; i++){
int x,y;
cin>>x>>y;
build(x,y);
build(y,x);
}
dfs(root,0);
for (int i=1; i<=n; i++) cout< 此种方法不仅适合二叉树,也适合多叉树。
四、已知先序和中序遍历顺序,建立二叉树。
LeetCode的题目:https://leetcode-cn.com/problems/zhong-jian-er-cha-shu-lcof/
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
例如前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
建立如下二叉树并返回根节点。
3
/ \
9 20
/ \
15 7
思路就是递归分治。 对于一个先序遍历序列,第一个一定是根节点,如样例的3。我们只要在中序遍历序列中找到这个3,那么3之前的都是左子树,之后的都是右子树。再依次递归处理即可。
因为题目说不含重复数字,所以在中序遍历中找根的这个工作可以借助哈希表。
还要注意,因为我们递归的是中序遍历的序列,所以还要再加一个参数用来记录此序列的先序遍历第一个是谁,也就是根节点是谁。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
unordered_map h;
TreeNode* buildTree(vector& preorder, vector& inorder) {
int n=inorder.size();
for (int i=0; i& preorder,vector& inorder,int l,int r,int g){
if (l>r) return NULL;
TreeNode* t=new TreeNode(preorder[g]); //构造函数
int j=h[preorder[g]]; //在inorder找pre[g]
t->left=build(preorder,inorder,l,j-1,g+1);
t->right=build(preorder,inorder,j+1,r,g+j-l+1);
return t;
}
};