基于Python的信号处理（1）——信号基础知识

【摘要】

• 使用Python进行信号处理
• 参考书目：《数字信号处理——原理、算法与应用》第四版
• 这是一个笔记，不一定全面
• 本文主题：数字信号基本知识

---

---

1. 信号的数学表达

1.1 连续时间正弦信号

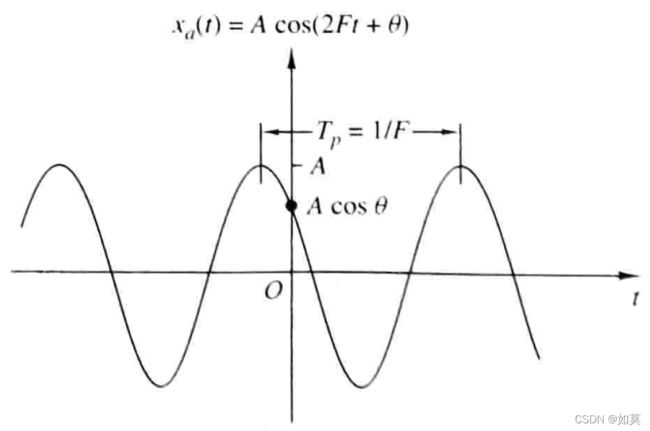
图1 模拟正弦信号及其参数

给定一个连续信号$$x_a(t)=A\text{cos}(\Omega t+\theta )$$它由三个参数完全表征：幅度$A$、频率$\Omega$、相位$\theta$，而下标$a$表示模拟信号。其中，$$\Omega =2\pi F$$
$F$为正弦函数周期的倒数（周期/秒），$F=1/T_p$，$T_p$为基本周期，如图1所示。此时有，
$$x_a(t)=A\text{cos}(2\pi Ft+\theta )$$
利用欧拉恒等式($j=\sqrt{-1}$)
$$e^{\pm j\varphi }=\text{cos}(\varphi )\pm j\text{sin}(\varphi )$$
得到信号的复指数形式
$$x_a(t)=\frac{A}{2}{e}^{j(\Omega t+\theta )}+\frac{A}{2}{e}^{-j(\Omega t+\theta )}$$

1.2 离散时间正弦信号

离散时间正弦信号
$$x(n)=A\text{cos}(\omega n+\theta ),-\infty <n<\infty$$

注意：这里的频率$\omega$是弧度/样本(rad/sample)，而$\theta$的单位是弧度(rad)。

定义
$$\omega =2\pi f$$
则信号表示为
$$x(n)=A\text{cos}(2\pi fn+\theta ),-\infty <n<\infty$$
信号是周期的，且最小周期$N$称为基本周期。

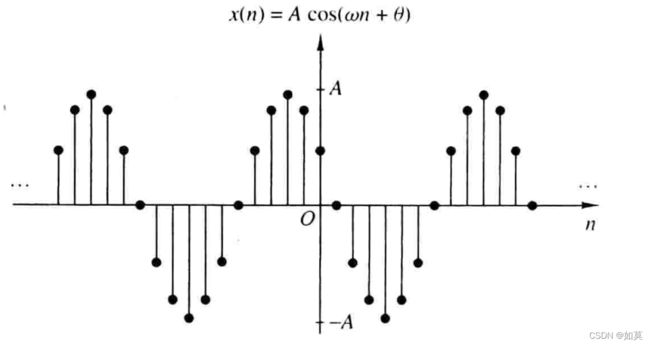
图2 离散正弦信号及其参数

图2显示了频率$\omega =\pi /6\text{rad}/s$(f=1/12周期/样本)，相位$\theta =\pi /3$的正弦信号。

离散时间信号特点:

• 最高震荡频率在$\omega =\pi$(或$\omega =-\pi$)或$f=1/2$(或$f=-1/2$)时达到。

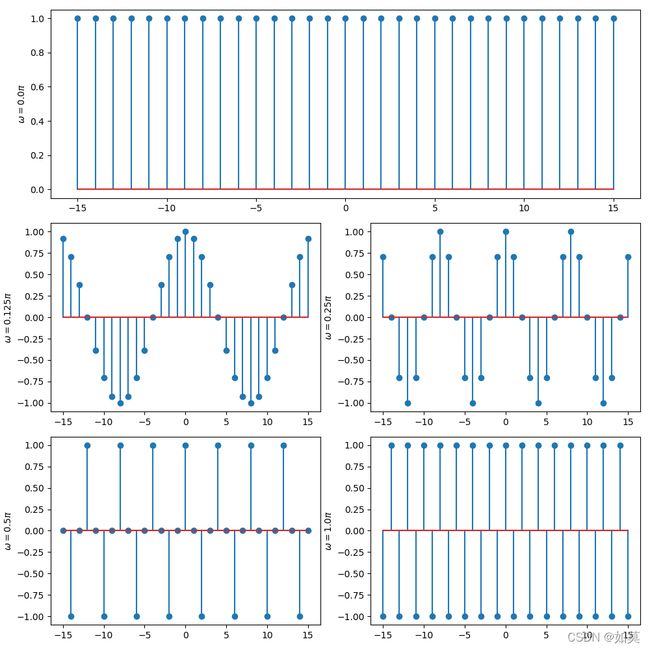
图3 不同频率对离散信号的影响

从图3可以看出，随着频率的增加，信号震荡逐渐加快。但是频率$\omega =\pi$时，震荡不在增加，此时$f=1/2$，即每两个相邻样本之间经历半个周期。
频率能不能更快呢？不行。离散信号本质上都是对连续信号采样的结果，根据奈奎斯特采样定理，采样频率至少为信号频率的2倍才能恢复信号。很明显，一个正弦波周期内，至少要两个点才能确定其周期大小。

2. 复指数信号与谐波

2.1 连续时间复指数信号

与频率${\Omega }_0$相关的连续时间谐波指数信号可以记为
$$s_k(t)=e^{jk{\Omega }_{0}t}=e^{j2\pi k{F}_{0}t},k=\pm 1,\pm 2,\cdots$$
其基本周期为$1/(k{F}_0)=Tp/k$，基本频率为$k{F}_0$。构造谐波相关的复指数信号的线性组合
$$x_a(t)=\sum _{-\infty }^{\infty }{c}_k{s}_k(t)=\sum _{-\infty }^{\infty }{c}_k{e}^{jk{\Omega }_{0}t}$$
其中$c_k$是任意复常数。上式为信号$x_a(t)$的傅里叶级数展开，信号$s_k(t)$称为第$k$次谐波。

2.2 离散时间复指数信号

设离散周期复指数序列的周期为$N$，则频率为$f_0=1/N$，谐波相关复指数为
$$s_k(n)=e^{j2\pi k{f}_{0}n},k=\pm 1,\pm 2,\cdots$$
基本周期为$N$的信号$x(n)$可以表示成傅里叶级数的形式
$$x(n)=\sum _{k=0}^{N-1}{c}_k{s}_k(n)=\sum _{k=0}^{N-1}{c}_k{e}^{j2\pi kn/N}$$
其中，复常数$\{c_k\}$为傅里叶系数。

3. 采样、模数/数模转换

模数转换(A/D)：

• 采样：采样间隔为$T$
• 量化：未量化样本$x_a(n)$，量化输出$x_q(n)$
• 编码：用$b$位二进制序列对量化输出$x_q(n)$进行编码

数模转换(D/A)：
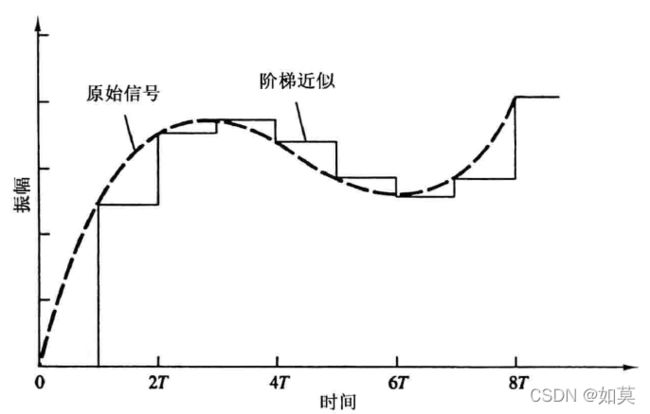
举一个简单的例子：零阶保持数模转换

图4 零阶保持数模转换

3.1 采样频率与信号频率之间的关系

图5 模拟信号的周期采样

• 采样周期：$T$
• 采样频率：$F_s=1/T$

设模拟信号的频率为$F$(或$\Omega$)，考虑正弦形式
$$x_a(t)=A\text{cos}(2\pi Ft+\theta )$$
采样($t=nT$)后为
$$x(nT)=A\text{cos}(2\pi FnT+\theta )=A\text{cos}(\frac{2\pi Fn}{F_s}+\theta )$$
因此

连续时间	离散时间信号
$\Omega =2\pi F$，弧度/秒，Hz	$\omega =2\pi f$，弧度/样本，周期数/样本
{}	$f=F/F_s$
{}	$\omega =\Omega T$
{}	$-\pi \le \omega \le \pi$
{}	$-\frac{1}{2}\le f\le \frac{1}{2}$
$-\infty \le \Omega \le \infty$	$-\frac{\pi }{T}\le \Omega \le \frac{\pi }{T}$
$-\infty \le F\le \infty$	$-\frac{F_s}{2}\le \omega \le \frac{F_s}{2}$

3.2 采样定理

采样定理：如果包含在某个模拟信号中$x_a(t)$中的最高频率是$F_{\text{max}}=B$，而信号以采样速率$F_s>2F_{\text{max}}=2B$采样，那么$x_a(t)$可以从样本值准确恢复，插值函数为sinc函数：
$$g(t)=\frac{\text{sin}(2\pi Bt)}{2\pi Bt}$$
而$x_a(t)$可以表示为
$$x_a(t)=\sum _{n=-\infty }^{\infty }{x}_a\left(\frac{n}{F_s}\right)g\left(t-\frac{n}{F_s}\right)$$
其中$x_a(n/F_s)=x_a(nT)=x(n)$是$x_a(t)$的样本。 采样频率$F_N=2B=2F_{\text{max}}$称为奈奎斯特频率。

图6 sinc函数形状

4. 实验代码

4.1 软件包

• 使用numpy生成信号
• 使用matplotlib画图

4.2 代码

• 绘制 图3 不同频率对离散信号的影响

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure(figsize=(10, 10))
a1 = plt.subplot2grid((3, 2), (0, 0), colspan=2)
a2 = plt.subplot2grid((3, 2), (1, 0))
a3 = plt.subplot2grid((3, 2), (1, 1))
a4 = plt.subplot2grid((3, 2), (2, 0))
a5 = plt.subplot2grid((3, 2), (2, 1))
ax = [a1, a2, a3, a4, a5]

n = np.linspace(-15, 15, 31)  # 信号样点
f = np.array([0, 1 / 16., 1 / 8., 1 / 4., -1 / 4.])  # 每个样点的基本周期
w = 2 * np.pi * f  # 角频率

for i in range(len(w)):
    y = np.cos(w[i] * n)  # 不同频率的信号
    ax[i].stem(n, y)  # 画图
    ax[i].set_ylabel('$\omega=$' + str(f[i] * 2) + '$\pi$')

plt.show()

• 绘制 图6 sinc函数形状

plt.figure(figsize=(10, 5.5))
t = np.linspace(-5, 5, 501)
sinc = np.sin(2 * np.pi * t) / (2 * np.pi * t)
plt.plot(t, sinc, 'b', linewidth=3)
plt.xlabel('time($s$)', fontsize=20)
plt.ylabel("$g(t)$", fontsize=20)
plt.text(1, 0.4, r'$ g(t)=\dfrac{\sin(2\pi t)}{2\pi t}} $', fontsize=20)
plt.grid(True)
plt.tight_layout()
plt.show()