数字信号处理及python实现(一)
这是参考知乎的数字信号处理及matlab实现的python实现版本,参考连接
冲激信号
δ ( n − n 0 ) = { 1 n = n 0 0 n ≠ n 0 \delta(n-n_0)=\begin{cases} 1 & n = n_0 \\ 0 & n \neq n_0 \end{cases} δ(n−n0)={10n=n0n=n0
test\signal.py中impseq函数
def impseq(self, n0, n1, n2):
"""返回冲激位移脉冲,[n1,n2]的信号
:param n0: 判断数值
:param n1: 下界
:param n2: 上界
:return:
"""
if n0 < n1 or n0 > n2 or n1 > n2:
raise ZeroDivisionError("参数必须满足n1<=n0<=n2")
n = np.array(list(range(n1, n2 + 1)))
x = []
for ni in n:
if ni == n0:
x.append(1)
else:
x.append(0)
return x, n
单元测试函数
def test_impseq(self):
n = list(range(-5, 6))
signal = Signal()
s1 = signal.impseq(-2, -5, 5)[0]
s1 = list(map(lambda x: x * 2, s1))
s2 = np.array(signal.impseq(4, -5, 5)[0])
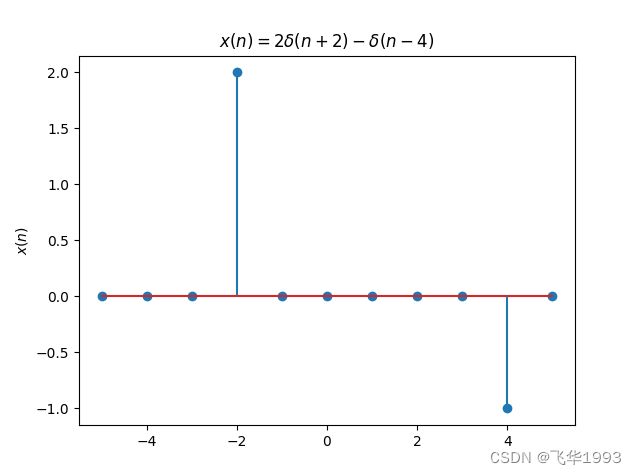
x = np.array(s1) - np.array(s2)
plt.stem(n, x.tolist())
plt.title('$x(n)=2\delta(n+2)-\delta(n-4)$')
plt.ylabel('$x(n)$')
plt.savefig('data/images/1.png')
正弦序列
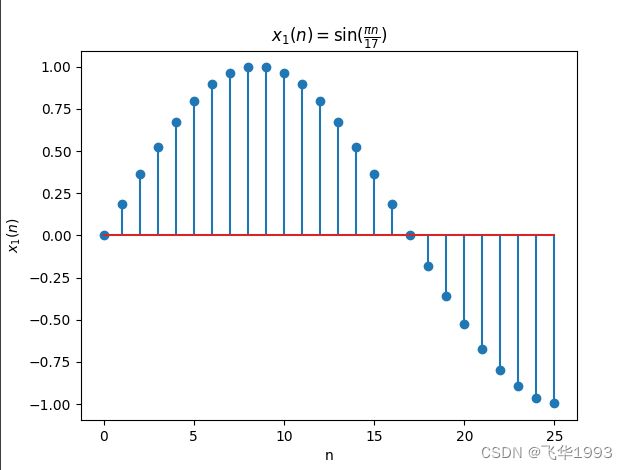
a. x 1 ( n ) = sin ( π n 17 ) , 0 ≤ n ≤ 25 x_1(n)=\sin(\pi\frac{ n}{17}),0\leq n\leq 25 x1(n)=sin(π17n),0≤n≤25
b. x 2 ( n ) = sin ( π n 17 ) , − 15 ≤ n ≤ 25 x_2(n)=\sin(\pi\frac{n}{17}),-15\leq n\leq 25 x2(n)=sin(π17n),−15≤n≤25
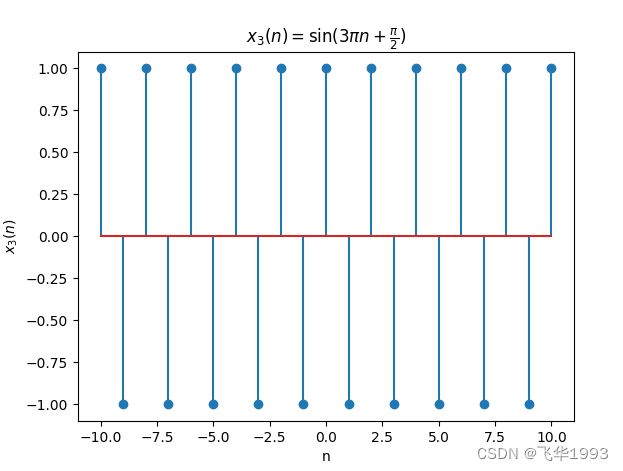
c. x 3 ( n ) = sin ( 3 π n + π 2 ) , − 10 ≤ n ≤ 10 x_3(n)=\sin(3\pi n+\frac{\pi}{2}),-10\leq n\leq 10 x3(n)=sin(3πn+2π),−10≤n≤10
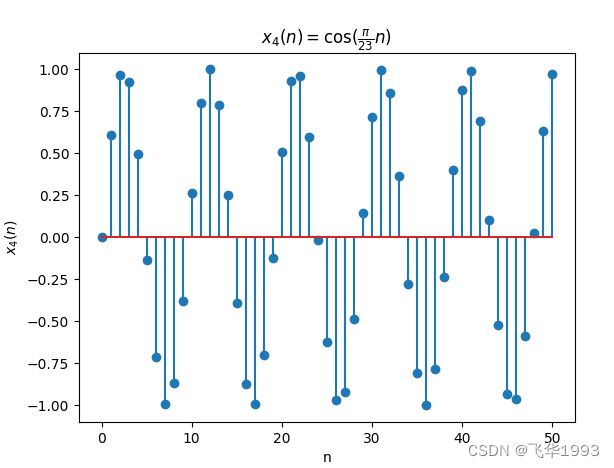
d. x 4 ( n ) = cos ( π 23 n ) , 0 ≤ n ≤ 50 x_4(n)=\cos(\frac{\pi}{\sqrt{23}}n),0\leq n\leq 50 x4(n)=cos(23πn),0≤n≤50
python代码a
test\signal.py中a函数
def a(self):
n = np.array(list(range(0, 26)))
x = np.sin(np.pi / 17 * n)
return x, n
单元测试函数
def test_a(self):
signal = Signal()
x,n = signal.a()
plt.stem(n, x.tolist())
plt.title(r'$x_1(n)=\sin(\frac{\pi n}{17})$')
plt.xlabel('n')
plt.ylabel('$x_1(n)$')
plt.savefig('data/images/a.png')
python代码b
test\signal.py中b函数
def b(self):
n = np.array(list(range(0, 41))) - 15
x = np.sin(np.pi / 17 * n)
return x, n
单元测试函数
def test_b(self):
signal = Signal()
x, n = signal.b()
plt.stem(n, x.tolist())
plt.title(r'$x_2(n)=sin(\frac{\pi n}{17})$')
plt.xlabel('n')
plt.ylabel('$x_2(n)$')
plt.savefig('data/images/b.png')
python代码c
test\signal.py中c函数
def c(self):
n = np.array(list(range(0, 21))) - 10
x = np.sin(np.pi * 3 * n + np.pi / 2)
return x, n
单元测试函数
def test_c(self):
signal = Signal()
x, n = signal.c()
plt.stem(n, x.tolist())
plt.title(r'$x_3(n)=\sin(3\pi n+\frac{\pi}{2})$')
plt.xlabel('n')
plt.ylabel('$x_3(n)$')
plt.savefig('data/images/c.png')
python代码d
test\signal.py中d函数
def d(self):
n = np.array(list(range(0, 51)))
x = np.sin(np.pi / np.sqrt(23) * n)
return x, n
单元测试函数
def test_d(self):
signal = Signal()
x, n = signal.d()
plt.stem(n, x.tolist())
plt.title(r'$x_4(n)=\cos(\frac{\pi}{23}n)$')
plt.xlabel('n')
plt.ylabel('$x_4(n)$')
plt.savefig('data/images/d.png')
指数序列
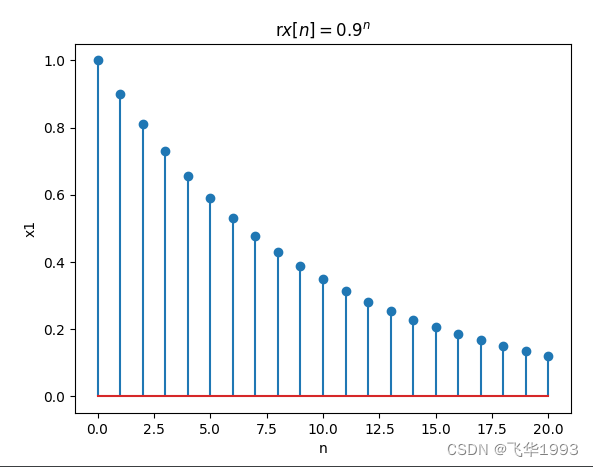
在区间 n = [ 0 , 20 ] n=[0,20] n=[0,20]上绘制指数信号 x [ n ] = 0. 9 n x[n]=0.9^n x[n]=0.9n
test\signal.py中genexp函数
def genexp(self, b, n0, L):
if L <= 0:
raise ZeroDivisionError("GENEXP:长度不是正数")
nn = n0 + np.array(list(range(0, L + 1)))
y = [b ** i for i in nn]
return y
单元测试函数
def test_genexp(self):
signal = Signal()
L = 20
nn = np.array(list(range(0,21)))
x1 = signal.genexp(0.9, 0, L);
plt.stem(nn, x1)
plt.xlabel('n')
plt.ylabel('x1')
plt.title('r$x[n]=0.9^n$')
plt.savefig('data/images/genexp.png')
复值信号
单元测试函数
def test_comp(self):
nn = np.array(list(range(0,26)))
f = np.exp((complex(0, 1))*nn/3)
plt.subplot(211)
plt.stem(nn,np.real(f))
plt.title('REAL PART')
plt.xlabel('INDEX(n)')
#plt.plot(nn, np.real(f))
plt.subplot(212)
plt.stem(nn,np.imag(f))
plt.title('IMAG PART')
plt.xlabel('INDEX(n)')
plt.tight_layout()
plt.savefig('data/images/comp.png')
复指数信号
单元测试函数
def test_comp_genexp(self):
n = np.array(list(range(0,21)))
A = 0.9
a = 0
b = np.pi / 4
x = A*np.exp((complex(a, b)) * n)
plt.subplot(211)
plt.stem(n, np.real(x))
plt.title('REAL PART')
plt.xlabel('INDEX(n)')
# plt.plot(nn, np.real(f))
plt.subplot(212)
plt.stem(n, np.imag(x))
plt.title('IMAG PART')
plt.xlabel('INDEX(n)')
plt.tight_layout()
plt.savefig('data/images/comp_genexp.png')