文献笔记|跨域节点分类|ACDNE|Adversarial Deep Network Embedding for Cross-network Node Classification

Adversarial Deep Network Embedding for Cross-network Node Classification

题目：基于对抗性深度网络嵌入的跨网络节点分类

作者：Xiao Shen, Quanyu Dai, Fu-lai Chung, Kup-Sze Choi

来源：AAAI 2020

单位：香港理工大学

挑战

现有的域自适应算法普遍无法对网络结构信息进行建模，当前的网络嵌入模型主要针对单网络应用。

方法概述

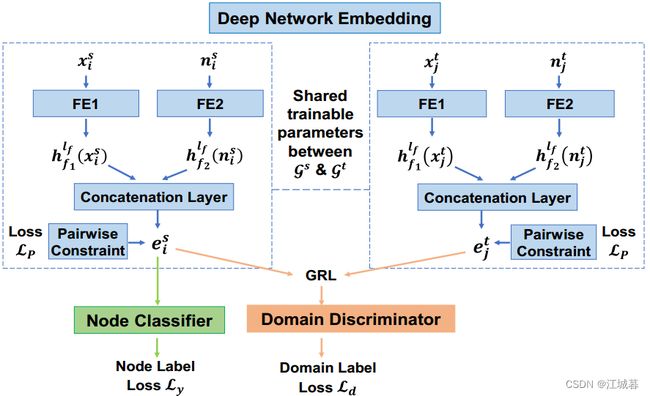
给定一个具有完全标记节点的源网络和一个具有完全未标记节点的目标网络，我们的目标是学习合适的节点表示，基于这些表示，可以成功地利用来自源网络的大量标记数据来分类目标网络中的节点。为此，提出了一种对抗性跨网络深度网络嵌入(ACDNE)模型，创新性地将深度网络嵌入与对抗性域适应相结合。所提出的深度网络嵌入模块包含两个特征提取器，这两个特征提取器分别基于每个节点自身的属性和由相关联的拓扑邻近度加权的其邻居的属性来学习节点表示。然后，节点之间的属性亲合性和拓扑邻近性可以被很好地保留。利用相同的深度网络嵌入模块(即，共享的可训练参数)来生成源网络和目标网络的节点表示。此外，节点分类器由ACDNE并入，以利用来自源网络的监督信号来使节点表示对于节点分类具有标签区分性。

为了解决跨网络的分布差异，ACDNE结合了域鉴别器来与深度网络嵌入模块竞争。一方面，域鉴别器试图区分源网络的节点表示和目标网络的节点表示。另一方面，深度网络嵌入模块被训练来学习网络不变节点表示，以欺骗域鉴别器。最后，ACDNE可以获得标签区分和网络不变的节点表示，从而有效地解决跨网络节点分类问题。

问题定义

令$\mathcal{G}=(V,E,A,X,Y)$表示一个有着节点集合$V$和边集$E$的网络。$A\in R^{n\times n},X\in R^{n\times w},Y\in R^{n\times c}$ 表示 $\mathcal{G}$ 的拓扑邻接矩阵、节点属性矩阵和节点标签矩阵，其中$n$表示节点数，$w$表示节点属性数，$c$表示$\mathcal{G}$中节点标签的数量。$A,X,Y$的第$i$行用$a_i,x_i,y_i$表示，它们分别表示节点$v_i\in V$的拓扑邻接、属性和可观察的标签。在跨网络节点分类问题中，我们有一个完全标记的源网络${\mathcal{G}}^s=(V^s,E^s,A^s,X^s,Y^s)$和一个未标记的目标网络${\mathcal{G}}^t=(V^t,E^t,A^t,X^t)$，其中两个网络的标签类别应当是相同的。另外，${\mathcal{G}}^s$和${\mathcal{G}}^t$没有公共节点且两个网络没有边相连。当两个网络没有共享相同的节点属性集时，可以在来自源网络和来自目标网络的属性之间构建联合属性集。然后，跨网络嵌入可以基于联合属性集去学习。注意，网络连接性的数据分布，节点属性和节点标签在跨网络中通常是不同的。跨网络节点分类的目标是学习适当的节点表示，基于这些表示，来自源网络的大量标记信息可以被成功地利用来预测目标网络的节点标记。

ACDNE

Deep Network Embedding

深度网络嵌入模块包含两个特征提取器、串联层和成对约束。

Feature Extractors

FE1 with $l_f$ hidden layers is constructed as:
$$h_{f_1}^{(k)}(x_i)=ReLU(h_{f_1}^{(k-1)}(x_i)W_{f_1}^{(k)}+b_{f_1}^{(k)}),1\le k\le l_f,\text{\hspace{1em}(1)}$$
其中$h_{f_1}^{(0)}(x_i)=x_i\in R^{1\times w}$表示输入$v_i$的属性向量。$x_{ik}$是$v_i$的第$k$个属性，并且$x_{ik}=0$表示$v_i$与第$k$个属性无关。$h_{f_1}^{(k)}(x_i)\in R^{1\times f(k)},1\le k\le l_f$表示$v_i$通过FE1的第$k$个隐藏层学习得到的潜在节点属性表示，$f(k)$是FE1的第$k$个隐藏层的维度。$W_{f_1}^{(k)}$和$b_{f_1}^{(k)}$表示FE1中第$k$层的待学习的权重和偏参数。$ReLU(\cdot )$是非线性的激活函数，它以$ReLU(x)=\max (0,x)$为特征。

FE2 with $l_f$ hidden layers is constructed as:
$$h_{f_2}^{(k)}(n_i)=ReLU(h_{f_2}^{(k-1)}(n_i)W_{f_2}^{(k)}+b_{f_2}^{(k)}),1\le k\le l_f,\text{\hspace{1em}(2)}$$
其中$h_{f_1}^{(0)}(n_i)=n_i\in R^{1\times w}$表示输入$v_i$的邻居属性向量。为了计算$n_i$，我们通过向更近的邻居分配更高的权重（即，拥有与$v_i$更高的拓扑接近度）来聚集邻居的属性，如下所示:
$$n_{ik}=\sum _{j=1,j\ne i}^n\frac{a_{ij}}{{\sum }_{g=1,g\ne i}^n{a}_{ig}}{x}_{jk},\text{\hspace{1em}(3)}$$
其中$a_{ij}$表示$v_i$和$v_j$之间的拓扑接近度。在这项工作中，我们遵循(Cao, Lu, and Xu 2016; Shen et al 2019)采用PPMI指标来测量网络中$K$步内节点之间的拓扑邻近性。$a_{ij}$的正值越大，表示$v_i$和$v_j$之间的网络关系越密切，而$a_{ij}=0$表示$v_j$在$\mathcal{G}$中的$K$步内不是$v_i$的邻居。

Concatenation Layer

接下来，我们馈送由FE1学习的最深潜在节点属性表示，即$h_{f_1}^{(l_f)}(x_i)$，以及由FE2学习的最深潜在邻居属性表示，即$h_{f_2}^{(l_f)}(n_i)$到如下的级联层:
$$e_i=ReLU([h_{f_1}^{(l_f)}(x_i),h_{f_2}^{(l_f)}(n_i)]W_c+b_c),\text{\hspace{1em}(4)}$$
其中$e_i\in R^{1\times d}$表示ACDNE最终学习的$v_i$的节点表示，$d$是嵌入维数。

• 一方面，通过利用每个节点自己的属性作为FE1的输入，共享相似属性的节点将具有相似的潜在节点属性表示，无论它们是否具有网络连接。
• 另一方面，通过利用邻居的属性作为FE2中的输入，共享相似邻域的节点或其共享相似属性的邻居将具有相似的潜在邻居属性表示。

然后，通过整合由FE1和FE2学习的潜在表示来学习级联层之后的最终节点表示，可以很好地保持节点之间的属性亲和力和拓扑邻近性。

Pairwise Constraint

接下来，我们将以下成对约束合并到节点表示中，以显式保持每个网络中节点之间的拓扑邻近性:
$${\mathcal{L}}_p=\frac{1}{n^s}\sum _{v_i,v_j\in V^s}{a}_{ij}||e_i-e_j|{|}^2+\frac{1}{n^t}\sum v_i,v_j\in V^t{a}_{ij}||e_i-e_j|{|}^2,\text{\hspace{1em}(5)}$$
其中$n_s$和$n_t$分别表示${\mathcal{G}}^s$和${\mathcal{G}}^t$的节点数。通过最小化${\mathcal{L}}_p$，源网络或目标网络中连接更强的节点将具有更相似的节点表示。为了简单起见，我们将与前述深度网络嵌入模块相关联的所有可训练参数表示为${\theta }_e=\{\{W_{f_1}^{(k)},b_{f_1}^{(k)},W_{f_2}^{(k)},b_{f_2}^{(k)}{\}}_{k=1}^{l_f},W_c,b_c\}$.

Node Classifier

为了使节点表示区分标签，我们通过在深度网络嵌入模块的顶部添加节点分类器来合并来自源网络的监督信号，如下所示:
$${\hat{y}}_i=\varphi (e_i{W}_y+b_y),\text{\hspace{1em}(6)}$$
其中${\hat{y}}_i\in R^{1\times c}$表示$v_i$在$c$个类别标签上的预测概率。$\varphi (\cdot )$是分类器的输出函数，它可以采用Softmax函数用于multi-class分类或者采用Sigmoid函数用于multi-lable分类。${\theta }_y=\{W_y,b_y\}$表示与节点分类相关的待训练的参数。通过使用源网络中所有带标签节点进行训练，Softmax交叉熵损失被定义成一个multi-classn节点分类，如下：
$${\mathcal{L}}_y=-\frac{1}{n^s}\sum _{v_i\in V^s}\sum _{k=1}^c{y}_{ik}\log ({\hat{y}}_{ik}),\text{\hspace{1em}(7)}$$
其中$y_{ik}$表示$v_i$的ground-truth标签，如果$v_i$与标签$k$相关，则$y_{ik}=1$，否则$y_{ik}=0$。${\hat{y}}_{ik}$表示$v_i$的在类别$k$下的预测概率。另外，对于multi-lable节点分类，one-vs-rest Sigmoid交叉熵损失被定义为：
$${\mathcal{L}}_y=-\frac{1}{n^s}\sum _{v_i\in V^s}\sum _{k=1}^c{y}_{ik}\log ({\hat{y}}_{ik})+(1-y_{ik})\log (1-{\hat{y}}_{ik}),\text{\hspace{1em}(8)}$$

Adversarial Domain Adaptation

接下来，我们采用一种对抗的域自适应方法来使ACDNE网络学习的节点表示不变。首先，可以将深度网络嵌入模块学习到的节点表示馈送给域鉴别器，以预测节点来自哪个网络，如下：
$$\begin{gathered} h_d^{(k)}(e_i)=ReLU(h_d^{(k-1)}(e_i)W_d^{(k)}+b_d^{(k)}),1\le k\le l_d, \\ \widehat{d_i}=Softmax(h_d^{l_d}(e_i)W_d^{(l_d+1)}+b_d^{(l_d+1)}),\text{\hspace{1em}(9)} \end{gathered}$$
其中$h_d^{(0)}(e_i)=e_i,h_d^{(k)}(e_i)\in R^{1\times d(k)}$表示$v_i$在域鉴别器的第$k$个隐藏层下所学习到的域表示，$d(k)$是第$k$个隐藏层的维度，$l_d$是域鉴别器中的隐藏层数。${\theta }_d=\{W_d^{(k)},b_d^{(k)}{\}}_{k=1}^{l_d+1}$表示域鉴别器中待训练的参数。然后，通过使用源网络和目标网络中的节点一同训练，域分类损失被定义成为：
$${\mathcal{L}}_d=-\frac{1}{n^s+n^t}\sum _{v_i\in \{V^S\cup V^t\}}(1-d_i)\log (1-{\hat{d}}_i)+d_i\log ({\hat{d}}_i),\text{\hspace{1em}(10)}$$
其中$d_i$是$v_i$的ground-truth域标签，如果$v_i\in V^t$则$d_i=1$，并且$v_i\in V^S$则$d_i=0$。${\hat{d}}_i$表示$v_i$来自目标网络的预测概率。为了使节点表示网络不变，域鉴别器和深度网络嵌入模块以对抗的方式相互竞争。

• 一方面，${\min }_{{\theta }_d}\{{\mathcal{L}}_d\}$使得域鉴别器能够准确地区分源网络的节点表示和目标网络的节点表示。
• 另一方面，${\min }_{{\theta }_d}\{-{\mathcal{L}}_d\}$使得深度网络嵌入模块被训练成通过跨网络不可区分的生成节点表示来欺骗域鉴别器。

Joint Training

通过集成深度网络嵌入、节点分类器和对立域适应，ACDNE的目标是优化以下minimax目标:
$$\underset{{\theta }_e,{\theta }_y}{\min }\{{\mathcal{L}}_y+p{\mathcal{L}}_p+\lambda \underset{{\theta }_d}{\max }\{-{\mathcal{L}}_d\}\},\text{\hspace{1em}(11)}$$
其中$p,\lambda$是平衡不同项效果的trade-off参数。在这项工作中，我们遵循(Ganin et al 2016)在深度网络嵌入模块和域鉴别器之间插入梯度反转层(GRL)，以便在反向传播期间同时更新它们。GRL对域分类损失${\mathcal{L}}_d$对网络嵌入参数${\theta }_e$的偏导数求逆，并将它们乘以系数$\lambda$。然后，可以通过随机梯度下降(SGD)优化ACDNE，如下所示：
$$\begin{gathered} {\theta }_e\leftarrow {\theta }_e-\mu \left(\frac{\partial {\mathcal{L}}_y}{\partial {\theta }_e}+p\frac{\partial {\mathcal{L}}_p}{\partial {\theta }_e}-\lambda \frac{\partial {\mathcal{L}}_d}{\partial {\theta }_e}\right), \\ {\theta }_y\leftarrow {\theta }_y-\mu \frac{\partial {\mathcal{L}}_y}{\partial {\theta }_y}, \\ {\theta }_d\leftarrow {\theta }_d-\mu \frac{\partial {\mathcal{L}}_d}{\partial {\theta }_d},\text{\hspace{1em}(12)} \end{gathered}$$
其中$\mu$表示学习率。算法1显示了ACDNE的训练过程。首先，在每个mini-batch中，我们分别从源网络和目标网络中抽取一半的节点。然后，在第3-10行中，使用相同的深度网络嵌入模块来学习两个网络的节点表示。然后，在行11-13中为每个小批量计算成对约束损失、节点分类损失和域分类损失。接下来，ACDNE的可训练参数由第14行中的SGD更新。在ACDNE最终收敛或达到最大训练迭代后，可以使用优化的网络嵌入参数${\theta }_e^{\ast }$来生成跨网络的标签区分和网络不变的节点表示，即$\{e_i^s{\}}_{i=1}^{n^s}$和$\{e_j^t{\}}_{j=1}^{n^t}$。接下来，优化的节点分类参数${\theta }_y^{\ast }$将被用在$\{e_j^t{\}}_{j=1}^{n^t}$上，以预测目标网络的节点标签。

实验