【神经网络】GAN:生成对抗网络
GAN:生成对抗网络
Generator(生成器)概念
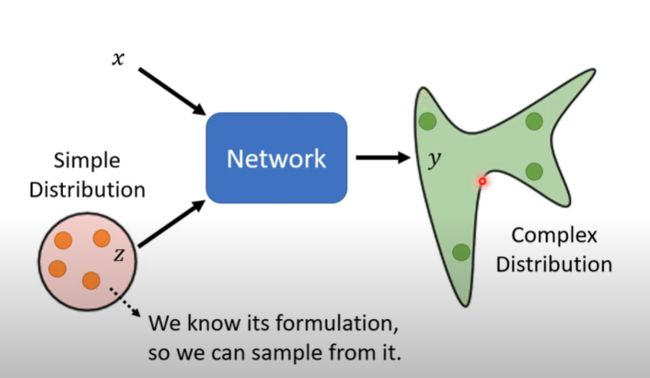 和传统的神经网络不同,Generator除了接受x的输入之外,还会接受一个简单的分布作为z进行输入,从而使得网络的输出也是一个复杂的分布
和传统的神经网络不同,Generator除了接受x的输入之外,还会接受一个简单的分布作为z进行输入,从而使得网络的输出也是一个复杂的分布
为什么输出需要时一个分布呢?以视频预测为例,比如说在糖豆人游戏中,我们需要预测视频的接下来的10帧是怎么样的

问题是传统的神经网络(NN)训练出来的结果,在拐角处,一个糖豆人会分裂为两个糖豆人,一个向左一个向右,这是因为在普通NN中,糖豆人向左和向右都有可能,是概率不同,因此他将这两个结果都显示了出来
更抽象地说,当我们的输出需要有一些“创造力”,也就是面对一个输入,需要有多个混合的输出的时候,我们就需要Generator,比如说在画图方面,同样输入“白发红瞳”,不同的人会画出不同的样子
因此其输入反而是一个相对低维度的向量,而输出是一个很高维度的向量。比如说一个一维向量代表了生成动漫人物的特征(发色、瞳距、表情等),而输出则是一张动漫图片,这肯定比输入要高纬度。刚开始的低维输入指的是x,而为了给生成器一个基准,我们还会输入一些动漫图片的采样,这个就是z
GAN
除了Generator之外,还需要一个Discriminator(鉴别器),他会输出一个数字,用于评判输出符合输入的程度。
以动画生成为例:
在GAN中,第一次迭代几乎是随机生成的,因此一般会生成一塌糊涂,而鉴别器则会给出很低的分数,比如鉴别器通过是否有眼睛判断是否是动漫
下一次迭代中,生成器会进行优化,尽量去满足第一代鉴别器的要求,使得在鉴别器Gen 1中得到较高的分数
而鉴别器也会进化,采用更加复杂的策略来进行评判
以此类推,不断进化,最后使得生成的结果越来越像输入x和z
进一步详细说明,刚开始我们会传入x和一个分布z到GAN中
Step 1
固定生成器,训练鉴别器
这个z实际上是一些动漫图片的采样,因为如果是纯随机生成的一代GAN,估计会跟电视坏了一样,因此给一些适当的基准是好的
接着我们用真正的动漫图片作为数据集1,并且对比数据集1和GAN生成的图片的差异,用这个去生成能够将真实数据(数据集1)和GAN生成图片分离开来的鉴别器
Step 2
固定鉴别器Discriminator ,训练生成器,使得生成器产生出来的图片能够“欺骗”鉴别器,因为鉴别器参数已经被固定了,所以生成器可以不断改变自身参数,生成出鉴别器更喜欢的图像,从而提高鉴别器分数
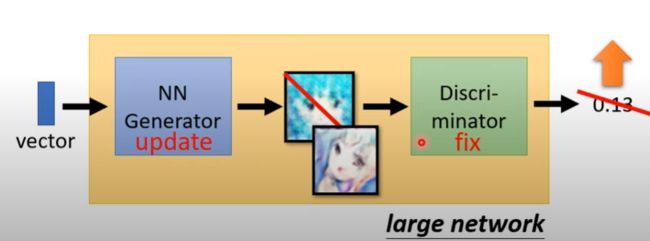
反复进行Step1和Step2,使得他们不断进化。也就是生成器不断调整参数使得它能够“欺骗”鉴别器,使得鉴别器认为它生成的图片就是一张真实的动漫图片;而鉴别器的任务则是仔细寻找生成图片和真实图片的区别,使得它能够区分生成的图
Generator详解
以一维向量为例,z作为一个随机采样的分布,他采样是相对平均的,而 P d a t a P_{data} Pdata表示的是真实数据,可以看到,经过生成器之后,生成出来的 P G P_G PG已经很接近 P d a t a P_{data} Pdata了

简单来说,生成器的评判标准和最优化反向,是让生成结果 P G P_G PG尽量接近 P d a t a P_{data} Pdata,公式如下
G ∗ = a r g m i n G D i v ( P G , P d a t a ) G^* = arg\:min_G\: Div(P_G, P_{data}) G∗=argminGDiv(PG,Pdata)
也就是要对G进行取值,使得Div(P_G, P_{data})最小,也就是使得 P G P_G PG和 P d a t a P_{data} Pdata更接近 。
对鉴别器D的训练也是如此,分别对 P G P_G PG和 P d a t a P_{data} Pdata进行采样。当 P G P_G PG和 P d a t a P_{data} Pdata中的点比较接近的时候, V ( D , G ) V(D,G) V(D,G)是较小的。但是对于鉴别器来说,他的任务是要将生成的图片和真实的图片区分开来,也就是 P G P_G PG和 P d a t a P_{data} Pdata分得越开越好,因此 m a x D V ( D , G ) max_D\:V(D,G) maxDV(D,G),也就是寻找参数D,使得 V ( D , G ) V(D,G) V(D,G)最大

实际上,在公式 G ∗ = a r g min G D i v ( P G , P d a t a ) G^* = arg\:\min_G\: Div(P_G, P_{data}) G∗=argminGDiv(PG,Pdata)中, D i v Div Div函数是很难计算的,但好消息是 D i v ( ) Div() Div()的结果和 m a x D V ( D , G ) max_D\:V(D,G) maxDV(D,G)是近似的(在此不作数学证明),因此 G ∗ G* G∗可以写作
G ∗ = a r g min G max D ( D , G ) G^* = arg\:\min\limits_{G}\: \max_D\:(D,G) G∗=argGminDmax(D,G)
也就是说,生成器要寻找参数G,使得 max D ( D , G ) \max_D\:(D,G) maxD(D,G)最小,而鉴别器需要寻找参数D,使得 D ( D , G ) D\:(D,G) D(D,G)最大。这就是GAN的对抗过程,对应上面介绍的step1和step2,因此方程G*就是GAN的最优化方程
GAN训练小技巧(施工中)
Wasserstein distance
对于 P G P_G PG和 P d a t a P_{data} Pdata,他们的重叠空间可能及其小。如果数据维度越高,那想要重合的难度也就越高。
第二个是因为在对 P G P_G PG和 P d a t a P_{data} Pdata处理的时候,我们都是进行采样处理,很难知道两个分布的全貌,这也使得两个分布明明是重叠的,但我们仅靠采样判断的话,看似是可以画一条线将他们分开的。 P G P_G PG和 P d a t a P_{data} Pdata部分重叠代表着生成器在当前G1的参数下生成的内容是和真实样本相近的,但是在鉴别器上,他看起来和完全无重叠的情况一样,也就是鉴别器会认为他们完全不相像,这会使得生成器认为G1参数很烂,从而不采用它
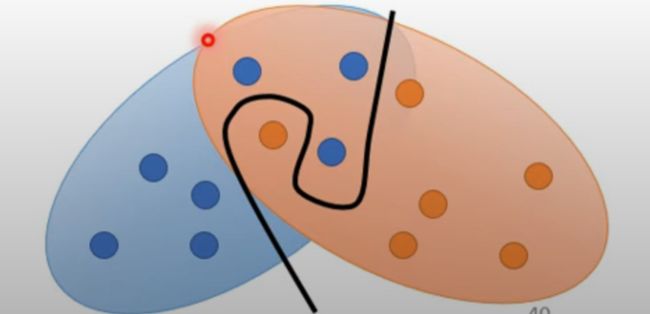
最简单的解决方案就是直接增加采样数量,但是这会增加训练时间
后来有一种新方法称之为Wasserstein distance
这种方法类似一种推土机,会整体地考虑两个点集之间的距离,而非直接使用二分,其最优化公式如下
max D ∈ 1 − L i p s c h i t z E x P d a t a [ D ( x ) ] − E x P G [ D ( x ) ] \max_{D\in1-Lipschitz}{E_{x~P_{data}}[D(x)]-E_{x~P_{G}}[D(x)]} D∈1−LipschitzmaxEx Pdata[D(x)]−Ex PG[D(x)]
GAN
GAN由生成器和鉴别器组成,这也导致只要有其中一方出现问题,就会导致整个系统瘫痪。