B站左程云算法视频基础提升04

树形DP

使用前提：如果题目求解目标是S规则，则求解流程可以定成以每一个节点为头结点的子树在S规则下的每一个答案，并且最终答案一定在其中。

二叉树的节点间的最大距离：

设以X为头结点的整棵树的最大距离分两种情况讨论：1）X不参与，要求返回的信息是左子树的最大距离maxdistance和右子树的最大距离maxdistance；2）X参与，左高度height+1+右高度height

返回值结构：maxdistance、height

maxdistance在左子树的最大距离maxdistance和右子树的最大距离maxdistance和左高度height+1+右高度height中取max

public static int maxDistance(Node head){
    return process(head)maxDistance;
}

public static class Info{
    public int maxDistance;
    public int height;
    public Info(int dis, int h){
        maxDistance = dis;
        height = h;
    }
}
//返回以x为头的整棵树的两个信息
public static Info process(Node x){
    if(x == null){
        return new Info(0,0);
    }
    Info leftInfo = process(x.left);
    Info rightInfo = process(x.right);
    //Info
    int p1 = leftInfo.maxDistance;
    int p2 = rightInfo.maxDistance;
    int p3 = leftInfo.height + 1 + rightInfo.height;
    int maxDistance = Math.max(p3, Math.max(p1,p2));
    int height = math.max(leftInfo.hight, rightInfo.height) + 1;
    return new Info(maxDistance, height);
}

套路：

一）以某节点X为节点的子树中，分析可能性（以X左、X右和X整棵树考虑）；

二）由一）列出所有的信息

三）合并二）的信息，对左和右提出同样的要求，并写出信息结构

四）设计递归函数，是以X为头的答案

        basecase

        默认得到在左树和右树所有信息

         所有可能性整合

         返回三）的信息结构

派对的最大快乐值（leetcode 337）

X参与：X乐+A不来的整棵树的最大快乐值+B不来的整棵树的最大快乐值+C不来的整棵树的最大快乐值

X不参与：0+max{A不来的整棵树的最大快乐值，A来的整棵树的最大快乐值}+max{B来的整棵树的最大快乐值，B来的整棵树的最大快乐值}+...

public static class Info{
    public int laiMaxHappy;
    public int buMaxHappy;
    public Info(int lai, int bu){
        laiMaxHappy = lai;
        buMaxHappy = bu;
    }
}

public static Info process(Employee x){
    if(x.nexts.isEmpty()){//x是基层员工
        return new Info(x.happy,0);
    }
    int lai = x.happy;
    int bu = 0;
    for(Employee next : x.nexts){
        Info nextInfo = process(next);
        lai += nextInfo.buMaxHappy;
        bu += Math.max(nextInfo.laiMaxHappy, nextInfo.buMaxHappy);
    }
    return new Info(lai,bu);
}

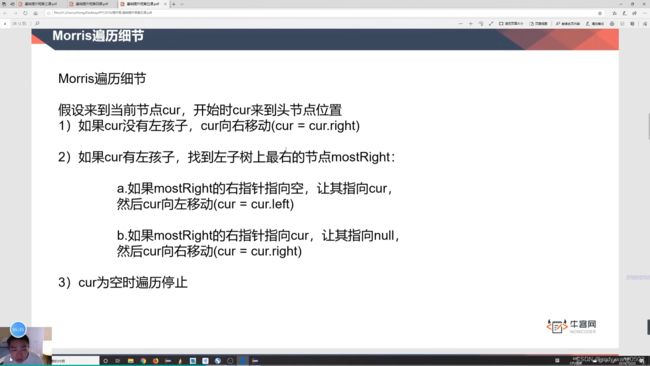
Morris遍历（通过来回标记遍历整棵树）

一种遍历二叉树的方式 时间复杂度o(N) 空间复杂度o(1)

利用原树中大量空闲指针的方式，达到节省空间的目的

 

无左树，只有一次到达自己

有左树，根据左树的最右节点指向判断第几次达到自己

public static void morris(Node head){
    if(head == null){
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while(cur != null){//过流程
        mostRight = cur.left;//mostRight是cur左孩子
        if(mostRight != null){//有左子树
            while(mostRight.right != null && mostRight.right != cur){
                mostRight = mostRight.right;
            } 
            //mostRight变成了cur左子树上，最右的节点
            if(mostRight.right == null){//第一次来到cur
                mostRight.right = cur;
                cur =cur.left;
                continue;
            }else{   //mostRight.right = cur 
                mostRight.right = null;
            }
        }
        cur = cur.right;
    }
}

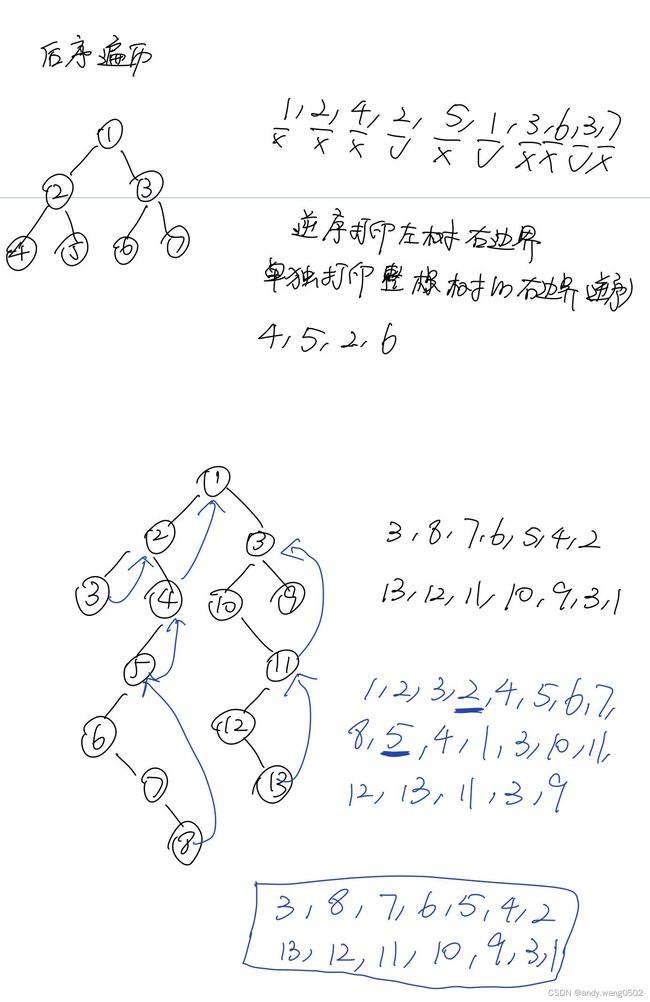
所有节点遍历自己的左子树右边界，总代价O(N)

 

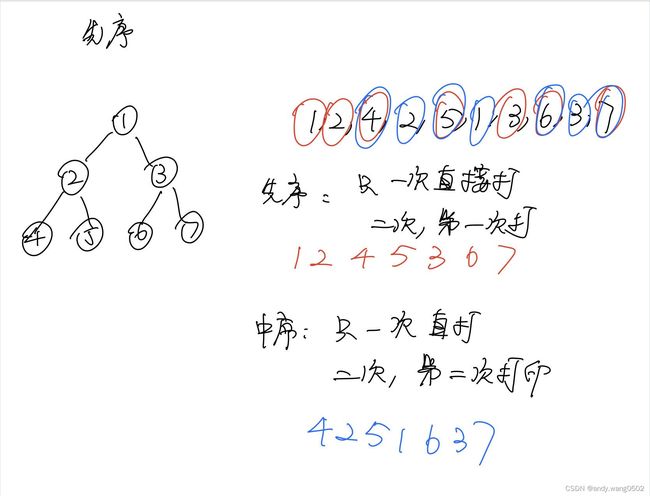
先序遍历和中序遍历

 

public static void morrisPre(Node head){
    if(head == null){
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while(cur != null){//过流程
        mostRight = cur.left;//mostRight是cur左孩子
        if(mostRight != null){//有左子树
            while(mostRight.right != null && mostRight.right != cur){
                mostRight = mostRight.right;
            } 
            //mostRight变成了cur左子树上，最右的节点
            if(mostRight.right == null){//第一次来到cur
                System.out.println(cur.value);
                mostRight.right = cur;
                cur =cur.left;
                continue;
            }else{   //mostRight.right = cur 
                mostRight.right = null;
            }
        }else{//没有左子树的情况
                System.out.println(cur.value);
            }
            cur = cur.right;
    }
}

public static void morrisin(Node head){
    if(head == null){
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while(cur != null){//过流程
        mostRight = cur.left;//mostRight是cur左孩子
        if(mostRight != null){//有左子树
            while(mostRight.right != null && mostRight.right != cur){
                mostRight = mostRight.right;
            } 
            //mostRight变成了cur左子树上，最右的节点
            if(mostRight.right == null){//第一次来到cur
                mostRight.right = cur;
                cur =cur.left;
                continue;
            }else{   //mostRight.right = cur 
                    mostRight.right = null;
            }
         }
            System.out.println(cur.value);
            cur = cur.right;
    }
}

后序遍历

 

//以X为头的树，逆序打印
public static void printEdge(Node X){
    Node tail = reverseEdge(X);
    Node cur = tail;
    while(cur != null){
        System.out.print(cur.value + " ");
        cur = cur.right;
    }
    reverseEdge(tail);
}

public static Node reverseEdge(Node from) {
    Node pre = null;
    Node next = null;
    while (from != null){
        next = from.right;
        from.right = pre;
        pre = from;
        from = next;
    }
    return pre;
}
public static void morrisPos(Node head){
    if(head == null){
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while(cur != null){//过流程
        mostRight = cur.left;//mostRight是cur左孩子
        if(mostRight != null){//有左子树
            while(mostRight.right != null && mostRight.right != cur){
                mostRight = mostRight.right;
            } 
            //mostRight变成了cur左子树上，最右的节点
            if(mostRight.right == null){//第一次来到cur
                mostRight.right = cur;
                cur =cur.left;
                continue;
            }else{   //mostRight.right = cur 
                    mostRight.right = null;
                    printEdge(cur.left);
            }
         }
            cur = cur.right;
    }
    printEdge(head);
    System.out.println();
}

判断一棵树是否是搜索二叉树？

原先的做法：中序遍历，看是否升序

现在：

public static void isBst(Node head){
    if(head == null){
        return true;
    }
    Node cur = head;
    Node mostRight = null;
    int preValue = Integer.MIN_VALUE;
    while(cur != null){//过流程
        mostRight = cur.left;//mostRight是cur左孩子
        if(mostRight != null){//有左子树
            while(mostRight.right != null && mostRight.right != cur){
                mostRight = mostRight.right;
            } 
            //mostRight变成了cur左子树上，最右的节点
            if(mostRight.right == null){//第一次来到cur
                mostRight.right = cur;
                cur =cur.left;
                continue;
            }else{   //mostRight.right = cur 
                mostRight.right = null;
            }
        }
        if(cur.value <= preValue){
            return false;
        }
        preValue = cur.value;
        cur = cur.right;
    }
    return true;
}

二叉树题目的最优解：如果要用第三次信息的强整合要用递归套路，如果不需要第三次信息的强整合morris遍历是最优解。

大数据题目：位图解决某一范围上数字的出现情况，并可以节省大量空间

32位无符号整数的范围是0~4，294，967，295，现在有一个正好包含40亿个无符号整数的文件，所以在整个范围中必然存在没出现过的数，可以使用最多1GB的内存，怎么找到所有未出现过的数？

进阶：内存限制为3KB，但是只用找到一个没出现过的数即可

range：0~-1

count:40亿

/8=500M

一个bit表现数出现过没有。

进阶：所有的内存生成一个无符号整性数组 int[]，3KB/4 =750 接近512，申请一个长度512的数组，把range分为长度为512的数组，一共/512 = 8388608，0位置上的值表示0~8388607上的数出现的次数，依次类推，等量的512份；一定存在某范围上的数不够8388608个，找到不够的区间，在该范围继续分成512份，继续过四十亿个数，还是有不够的，周而复始，能找到缺的数字

比如1，1/8388608 = 0，所以arr[0]++

利用词频统计一定不够来实现定位

（时间换空间）

假设只能申请有限几个变量，怎么确定没出现过的数字：

0~-1二分 左侧和右侧一定有一个不满，继续二分，能找到缺的数字，最多32次