B站左程云算法视频中级班2~3

题目一：给定一个整数n，代表二叉树的节点个数，返回能形成多少种不同的二叉树结构

public static int process(int n){
    if(n < 0){
        return 0;
    }
    if(n == 1){
        return 1;
    }
    if(n == 2){
        return 2;
    }
    
    int res = 0;
    for(int leftNum = 0; leftNum <= n - 1; leftNum++){
        int leftWays = process(leftNum);
        int rightWays = process(n - 1 - leftNum);
        res += leftWays * rightWays; 
    }
    return res;
}

 动态规划

public static int numTrees(int n){
    if(n < 2){
        return 1;
    }
    int[] dp = new int[n + 1];
    dp[0] = 1;
    for(int i = 1; i < n + 1; i++){//节点个数为i的时候
        for(int j = 0; j < i ; j++){//左侧节点个数为j-1， 右侧节点个数为i-j
            dp[i] += dp[j] * dp[i - j - 1];
        }
    }
    return dp[n];
}

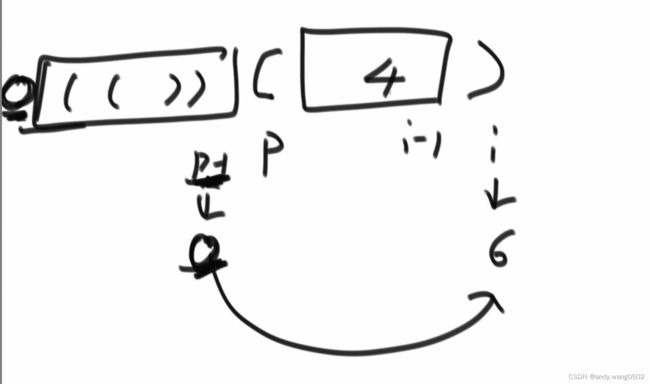
题目二：完整的括号字符串：有一个括号字符串S，现在需要在其中任意位置尽量少的添加括号，将其转化为一个完整的括号字符串。请问至少需要多少个括号

思路：遍历字符串，count = 0；遇到左括号，count++，右括号，count--

1）如果出现了count<0,字符串不完整

2）结束后，count=0，字符串完整

当count=-1，ans++，然后设count=0，继续遍历，最后ans+count就是结果

public static int needParentheses(String str){
    int count = 0;
    int ans = 0;
    for(int i = 0; i < str.length(); i++){
        if(str.charAt(i) == '('){
            count++;
        }else{
            if(count == 0){
                ans++;
            }else{
                count--;
            }
        }
    }
    return count + ans;
}

题目三：给定一个arr，求差值为k的去重数字对

哈希表

public static List> allPair(int[] arr, int k){
    HashSet set = new HashSet<>();
    for(int i = 0; i < arr.lengtj; i++){
        set.add(arr[i]);
    }
    List> res = new ArrayList<>();
    for(Integer cur : set){
        if(set.contains(cur + k)){
            res.add(Arrays.asList(cur, cur +k));
        }
    }
    return res;
}

题目四：给一个包含n个整数元素的集合a，一个包含m个整数元素的集合b

给定magic操作，从一个集合中取出一个元素，放到另一个集合里，且操作过后每个集合的平均值都大于操作前

问可以进行几次magic操作

注意点：1）不可把一个集合的元素取空，这就没有平均值了

                2）值为x的元素从集合b取出放入集合a，但集合a中已经有值为x的元素，则a的平均值不变（集合元素不会重复），但b的平均值可能会改变

情况1：   A ： 100    B ： 100   不拿

情况2：   A ： 50   B ： 100  A不拿

情况3：  A ： 100  B ： 50      拿大于50小于100的数

假设50~100之间的数有 60， 70， 80， 90 拿满足要求最小的数字（B中不存在，A不为空）

会使得A的平均值最大幅度上升，B的平均值最小幅度上升，使得magic的次数尽量多

//保证arr1无重复数字，arr2无重复数字，且arr1和arr2肯定有数字
public static int maxOps(int[] arr1, int[] arr2){
    double sum1 = 0;
    for(int i = 0; i < arr1.length; i++){
        sum1 += (double) arr1[i]; 
    }
    double sum2 = 0;
    for(int i = 0; i < arr2.length; i++){
        sum2 += (double) arr2[i];
    }
    if(avg(sum1, arr1.length) == avg(sum2, arr2.length)){
        return 0;
    }

    //平均值不等
    int[] arrMore = null;
    int[] arrLess = null;
    double sumMore = 0;
    double sumLess = 0;
    if(avg(sum1, arr1.length) > avg(sum2, arr2.length)){
        arrMore = arr1;
        sumMore = sum1;
        arrLess = arr2;
        sumLess - sum2;
    }else{
    arrMore = arr1;
        arrMore = arr2;
        sumMore = sum2;
        arrLess = arr1;
        sumLess - sum1;
    }
    Arrays.sort(arrMore);
    HashSet setLess = new HashSet<>();
    for(int num : arrLess){
        setLess.add(num);
    }
    int moreSize = arrMore.length; //平均值大的集合还剩几个数
    int lessSize = arrLess.length;//平均值小的集合还剩几个数
    int ops = 0;
    for(int i = 0; i < arrMore.length; i++){
        double cur = (double) arrMore[i];
        if(cur

题目五：最长有效子串

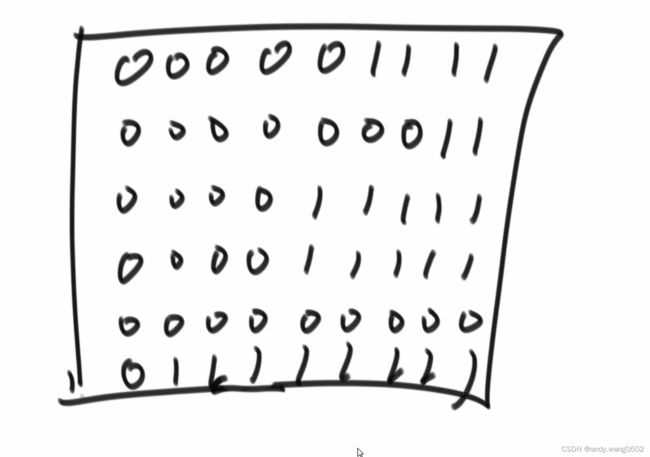
最大深度：遇到（，count++，遇到），count--，count的最大值就是最大深度

拓展：找到最长的有效括号子串

例如：（））（）（（））（）））（       为8

dp[                            ]

dp[i]：子串必须从i位置字符结尾，最长的有效长度是多少

（   ）（   ）（（   ））（  ））  ）  （  （      ））

  0 1     2  3    4   5  6 7   8  9  10  11  12  13  14  15

dp[0 ? 0 ? 0 0 ? ?  0 ???00??]

(    xxxx    )

        i-1   i

如果i-1 = 4，则 i= 6

 举例子

public static int maxLength(String s){
    if (s == null || s.equals("")){
        return 0;
    }
    char[] str = s.toCharArray();
    int[] dp = new int[str.length];
    int pre = 0;
    int res = 0;
    for(int i = 1; i < str.length; i++){
        if(str[i] == ')'){
              pre = i - dp[i - 1] - 1; //与str[i]配对的左括号的位置pre
              if(pre >= 0 && str[pre] == '('){
                    dp[i] = dp[i - 1] + 2 + (pre > 0 ? dp[pre - 1] : 0);
                } 
        }
        res = Math.max(res, dp[i]);
    }
    return res;
}

 题目6：请编写一个程序，对一个栈里的整型数据，按升序进行排序（即排序前，栈里的数据是无序的，排序后最大元素位于栈顶），要求最多只能使用一个额外的栈存放临时数据，但不得将元素复制到别的数据结构中

思路：准备一个辅助栈由小到大

题目七：将给定的数据转换成字符串：1转换成a，2转换成b

编写一个函数，给出可以转换的不同字符串的个数

str 来到i位置，即求i位置出发到最后能有多少种有效的字符串

 

public static int convertWays(int num) {
    if(num < 1){
        return 0;
    }
    return process(String.valueOf(num).toCharArray(),0);
}

//0..index-1已经转换完毕，并且转换正确
//str[index...]能转换出多少种有效的字符串表达
public static int process(char[] str, int index){
    if(index == str.length){
        return 1;
    }
    //index及其后续是还有数字字符的
    //0..
    if(str[index] == '0'){ //开头为0
        return 0;
    }
    // index及其后续是还有数字字符的，且不以0开头，以1~9开头
    int res = process(str, index + 1);//做了一个决定，就让str[index]自己作为一个部分
    if (index == str.length - 1){//除了index之外，后续没有字符串了
        return res;
    }
    //index+1依然没有越界
    //index 和index+1共同组成一个部分 <27
    if(((str[index] - '0') * 10 + str[index + 1] - '0') < 27) {
        res += process(str, index + 2);
    }
    return res;
}

简化

public static int dpWays(int num){
    if(num < 1){
        return 0;
    }
    char[] str = String.valueOf(num).toCharArray();
    int N = str.length;
    int[] dp = new int[N + 1];
    dp[N] = 1;
    dp[N - 1] = str[N - 1] == '0' ? 0 : 1;
    for(int i = N - 2; i >= 0; i--){
        if(str[i] == '0'){
            dp[i] = 0;
        }else {
            dp[i] = dp[i + 1]
                    + (((str[i] - '0') * 10 + str[i + 1] - '0') < 27 ? dp[i + 2] : 0);
        }
    }
    return dp[0];
}

题目八：

//全局变量，只在到达叶节点的时候，有可能更新
public static int maxSum = Integer.MIN_VALUE;

public static int maxPath(Node head) {
    p(head, 0);
    return maxSum;
}

//从根节点出发，到当前节点上方的节点，获得的路径和
public static void p(Node x, int pre){
    if(x.left == null && x.right == null){//   当前x是叶节点
        maxSum = Math.max(maxSum, pre + x.value);
    }
    if(x.left != null) {
        p(x.left, pre + x.value);
    }
    if(x.right != null){
        p(x.right, pre + x.value);
    }
}

套路解

//以x为头的整棵树上，最大路径和是多少，返回
//路径要求，一定从x出发，到叶节点，算作一个路径
public static int process2(Node x){
    if(x.left == null && x.right == null){
        return x.value;
    }
    int next = Integer.MIN_VALUE;
    if(x.left != null){
        next = process2(x.left);
    }
    if(x.right != null){
        next = Math.max(next, process2(x.right));
    }
    return x.value + next;
}

题目九：剑指offer04

给定一个元素为非负整数的二维数组matrix，每行和每列都是从小到大有序的。再给定一个非负整数aim，请判断aim是否在matrix中

拓展：返回1最多的一行