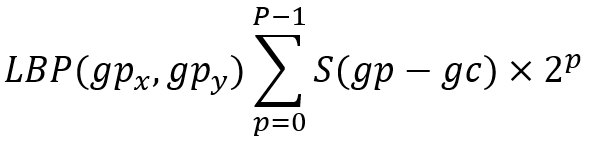二进制算法
介绍 ( Introduction)
The main idea behind LBP is to describe the neighborhood of image elements using binary codes. This method is usually used to study their local properties and identify the characteristics of individual parts of the image.
背后LBP 吨他的主要思想是描述使用二进制代码的图像元素的附近。 此方法通常用于研究其局部属性并识别图像各个部分的特征。
This algorithm is a combination of statistical and structural methods. It was first proposed by T. Ojala, M. Pietikanen, T. Mehpaa from Oulu University in Finland in 1994. It is considered a theoretically time-effective and straightforward method, showing excellent results in many studies.
该算法是统计方法和结构方法的组合。 它最初是由来自芬兰奥卢大学的T. Ojala, M。Pietikanen和T. Mehpaa于1994年提出的。它被认为是一种理论上有效且简单的方法,在许多研究中均显示出优异的结果。
如何运作❓ ( How it works❓)
As the name suggests, Local Binary Pattern (LBP for short) is a feature of the local representation of an image. It is composed of relative values by comparing each pixel with its neighboring pixels.
顾名思义,局部二进制模式( LBP )是图像局部表示的特征。 它是通过将每个像素与其相邻像素进行比较而由相对值组成的。
The main characteristics of LBP are:
LBP的主要特点是:
1-Low calculation cost
1-低计算成本
2-Resistance to fluctuations in image gray scale values
2-抵抗图像灰度值波动
A lot of improvements have been made since the first proposal in 1994. Especially in non-deep learning systems, it is widely used for facial image recognition, texture segmentation, and other image analysis applications.
自1994年提出第一个建议以来,已经进行了很多改进 。特别是在非深度学习系统中,它广泛用于面部图像识别,纹理分割和其他图像分析应用程序。
The LBP detects microstructures such as edges, lines, spots, flat areas, which can be estimated by the histogram.
LBP检测可以通过直方图估计的微观结构,例如边缘,线条,斑点,平坦区域。
* LBP方法步骤* (*LBP method steps*)
image by the author 作者形象1- Convert the image into grayscale space.
1-将图像转换为灰度空间。
2- For each pixel(gp) in the image, select the P neighborhoods that surround the central pixel. the coordinates of gp are given by
2-对于图像中的每个像素(gp),选择围绕中心像素的P个邻域。 gp的坐标为
(gc_x-Rsin(2πp/P),gc_y + Rcos(2πp/P))3- Take the center pixel (gc) and set it as a threshold for its P neighbors.
3-取中心像素(gc)并将其设置为其P邻居的阈值。
4- Set to 1 if the value of the adjacent pixel is greater than or equal to the value of the center pixel, 0 otherwise.
4-如果相邻像素的值大于或等于中心像素的值,则设置为1,否则设置为0。
5- Now compute the LBP value: Sequentially counterclockwise, write a binary number consisting of digits adjacent to the center pixel. This binary number (or its decimal equivalent) is called LBP-central pixel code and, further, is used as a characteristic selected local texture.
5-现在计算LBP值:逆时针顺序写一个二进制数字,该数字由与中心像素相邻的数字组成。 该二进制数(或其十进制等效数)称为LBP中心像素代码,并且进一步用作特征选择的局部纹理。
Uniform LBP formula 统一的LBP公式gc- the intensity value of the central pixel
gc-中心像素的强度值
gp- the intensity of the neighboring pixel with index p
gp-索引为p的相邻像素的强度
the function S can be expressed as:
函数S可以表示为:
P- number of sampling points on a circle of radius R(circular neighborhood).
P-半径为R(圆形邻域)的圆上的采样点数。
P- controls the quantization of the method.
P-控制方法的量化。
R- determines the spatial resolution of the method or operator.
R-确定方法或运算符的空间分辨率。
The gray values of neighbors which do not fall exactly in the center of a pixel(block) are estimated by interpolation.
通过内插来估计未完全落入像素(块)的中心的邻居的灰度值。
*详细示例* (*Detailed example*)
Now let’s take, for instance, the following chunk of a grayscale image:
现在,让我们以灰度图像的以下块为例:
image by the author 作者形象you can express the size of this window(3x3) in terms of The radius of the circle which equals to (2*R + 1), if the radius is 1, then we get a 3x3 matrix.
您可以用以下公式表示此窗口的大小(3x3):圆的半径等于(2 * R + 1),如果半径为1,则得到3x3矩阵。
The coordinates of the central pixel denoted by gc(gc_x,gc_y) is (1,1) according to the coordinated axis of the matrix(3x3). The value of this pixel is 33(center) gc =33. Let’s take for our example 8 neighbor samples (P=8). The coordinates of each sample point can be expressed as
根据矩阵(3x3)的坐标轴,由gc(gc_x,gc_y)表示的中心像素的坐标为(1,1)。 该像素的值为33(中心)gc = 33。 我们以8个邻居样本(P = 8)为例。 每个采样点的坐标可以表示为
(gc_x-Rsin(2πp/P),gc_y + Rcos(2πp/P))P = 8
P = 8
p = 0, 1 ,2 …,P-1
p = 0,1,2…,P-1
gc_x = gc_y = 1
gc_x = gc_y = 1
So for the previous matrix, we have the following coordinates for each sample:
因此,对于先前的矩阵,每个样本具有以下坐标:
(gp_x,gp_y)(g0_x,g0_y) => (1.0, 2.0)(g1_x,g1_y) =>(0.2929, 1.7071)...(g7_x,g7_y) =>(1.7071, 1.7071)Lets denote by Theta_i = 2πp/P => Theta=
让我们用Theta_i =2πp/ P => Theta =来表示
0pi/4pi/23pi/4pipi+pi/43pi/27pi/4Now we need to compare, as the formula suggests, the intensity of each neighbor pixel with the intensity of the central one, gc.
现在,如公式所示,我们需要将每个相邻像素的强度与中心像素gc的强度进行比较。
g0 = 80g1 = ?(on the circle at angle pi/4)g2 = 41g3 = ?g4 = 29g5 = ?g6 = 56g7 = ?g0 = 80 > gc = 33 ==> put 1g2 = 41 > gc = 33 ==> put 1g4 = 29 < gc = 33 ==> put 0g6 = 56 > gc = 33 ==> put 1Now the problem is to find the intensity values of g1, g3, g5, g7
现在的问题是找到g1,g3,g5,g7的强度值
In order to find these values, the paper suggests applying an interpolation.
为了找到这些值, 本文建议应用插值。
Since we have a 2d space(2-dimensional image), so we need a 2d interpolation method.
由于我们有一个二维空间(二维图像),因此我们需要一个二维插值方法。
Now one of the methods that I do remember from my education in numerical analysis is the bilinear interpolation.
现在,我从数学分析中学到的一种方法是双线性插值。
*双线性插值* (*bilinear interpolation*)
The term Interpolation is a way to calculate the intermediate value of a function from several of its already known values.
术语插值是一种从函数的多个已知值中计算函数的中间值的方法。
Bilinear interpolation is a linear interpolation of the function of two variables, that is, four-point interpolation. If the values of the function at these points are known f(x1,y1),f(x2,y1),f(x1,y2),f(x2,y2)
双线性插值是两个变量的函数的线性插值,即四点插值。 如果这些点的函数值已知f(x1,y1),f(x2,y1),f(x1,y2),f(x2,y2)
*Vectorization*It is reasonable to assume that the value at some point (x, y) located in the square bounded by these points can be found by interpolating twice, first by the x coordinate for two pairs of points, and then by the y coordinate, using the previous result.
*矢量化*合理地假设,可以通过两次插值(首先是两对点的x坐标,然后是y)来找到位于这些点所包围的正方形中的某个点(x,y)的值坐标,使用先前的结果。
In order to compute the intensity of g1, g3, g5, g7, we need to find the coordinates of the outer box containing the unknown pixel value.
为了计算g1,g3,g5,g7的强度,我们需要找到包含未知像素值的外框的坐标。
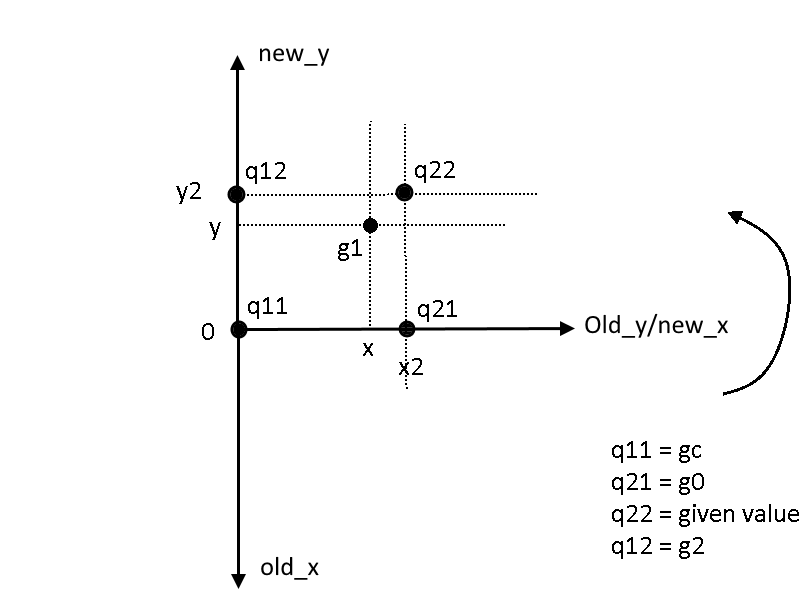
So for example, g1, which lies in between theta = 0 and theta = pi/2, the figure would looks like the following:
因此,例如,位于theta = 0和theta = pi / 2之间的g1,该图将如下所示:
image by the author 作者形象The pixel value of g1 can be interpolated using the formulas:
可以使用以下公式对g1的像素值进行插值:
Back to our example:
回到我们的例子:
[[25 41 24][29 33 80][38 56 65]]q11 = gc = 33q21 = 80q22 = 24q12 = 41We can translate the coordinated system to the origin => this will imply that
我们可以将协调系统转换为原点=>这意味着
x1=y1=0(origin point)
x1 = y1 = 0(原点)
x2=y2=1(one pixel away from the center in both axis)
x2 = y2 = 1(两个轴的中心距离一个像素)
x and y values of the unknown point need to be translated into the regular coordinated system(90 degrees counterclockwise rotation, which means new_x = old_y and new_y = - old_x )
未知点的x和y值需要转换为常规坐标系(逆时针旋转90度,这意味着new_x = old_y和new_y =-old_x)
applying this formula on the unknow samples we can find :
将这个公式应用于未知样本,我们可以找到:
g1 = 39 (this seems to be logically true, because it lies inside the boundries 33 , 80, 24, 41)g3 = 29g5 = 39g7 = 63Now the threshold matrix is equal to:
现在,阈值矩阵等于:
now applying the LBP formulas
现在应用LBP公式
LBP = (2⁰)*1 + (2¹)*1 + (2²)*1 +(2³)*0 +(2⁴)*0 +(2⁵)*1 +(2⁶)*1+ (2⁷)*1 = 1 + 2 + 4 + 32 + 64 + 128 = 231
LBP =(2⁰)* 1 +(2¹)* 1 +(2²)* 1 +(2³)* 0 +(2⁴)* 0 +(2⁵)* 1 +(2⁶)* 1 +(2⁷)* 1 = 1 + 2 + 4 + 32 + 64 + 128 = 231
image by the author 作者形象This process will repeat for each block of the image (along x and y axes)
对于图像的每个块(沿x和y轴)将重复此过程
⚠️ Note that the size of the image is reduced by a factor of 2*R lines and 2*R columns like in our example we have a 9x9 image would result in a 7x7 image (R=1 for this example)
⚠️请注意,图像的大小减少了2 * R行和2 * R列,例如在我们的示例中,我们有一个9x9的图像会导致7x7的图像(在此示例中R = 1)
In order to find if a pixel needs an interpolation or not, we can compute the fractional part of gpx and gpy, if the fractional part for both x and y is zero(like g0, g2, g4, g6) then, the pixel lies perfectly in the center of the block, otherwise we need to do an interpolation(g1, g3, g5, g7). For this example we have 4 pixels needs to perform the bilinear interpolation, and the other four points don’t need it since the value of this pixel is already given by the matrix.
为了确定像素是否需要插值,我们可以计算gpx和gpy的小数部分,如果x和y的小数部分均为零(例如g0,g2,g4,g6),则该像素位于完美地位于块的中心,否则我们需要进行插值(g1,g3,g5,g7)。 对于此示例,我们有4个像素需要执行双线性插值,而其他四个点则不需要它,因为此像素的值已由矩阵给出。
*伪代码* (*Pseudo-code*)
TO implement this method in python for the purpose of the visualization of the LBP, you are required 3 for loops :
为了在LBP中实现此方法以实现LBP的可视化,需要3个for循环:
For i in height range:
For j in width range:
Select a chunck of the image to compute its LBP value
For each block neighbors:
check if interpolation is needed
Compute_LBP(bock)
Add the result
Update the matrix with the value of LBPFor python implementation, you can check out my code on GitHub, under Visualize_LBP class.
对于python实现,您可以在GitHub的 Visualize_LBP类下签出我的代码。
*矢量化* (*Vectorization*)
Vectorization is the core of the internal implementation of NumPy. Vectorization is the absence of an explicit loop in code development. The loops themselves cannot be avoided, but their internal implementation is replaced with other constructs in the code.
向量化 是NumPy内部实现的核心。 向量化是代码开发中没有显式循环的条件。 循环本身是不可避免的,但是其内部实现被代码中的其他构造所替代。
The vectorization application makes the code more capacious and readable. Thanks to vectorization, many operations take a more mathematical form. For example, NumPy allows you to express the multiplication or addition of two matrices like this:
矢量化应用程序使代码更加宽敞和可读。 由于矢量化,许多运算采用了更数学的形式。 例如,NumPy允许您表达两个矩阵的乘法或加法,如下所示:
C = A*BC = np.add(A, B, casting="unsafe")
#if A and B have two different types(like int16,float32), use casting="unsafe"Now we can write our program using only one for loop to cycle through the neighbors' samples
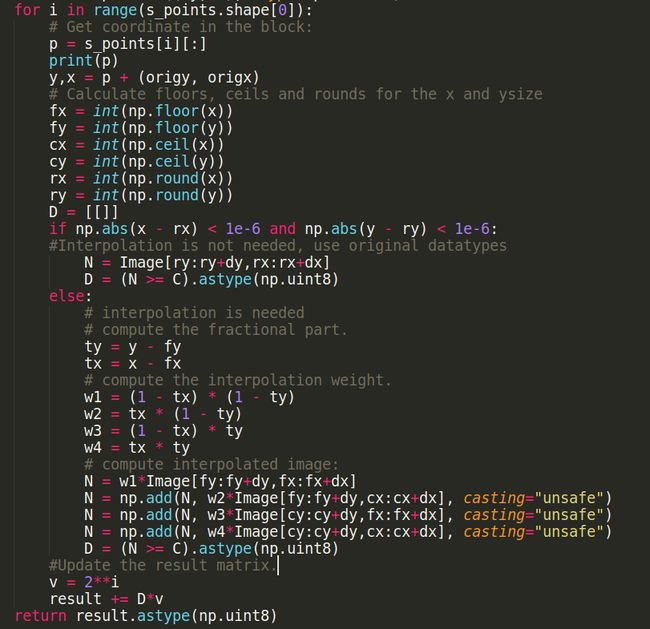
现在我们可以只使用一个for循环来编写程序,以循环浏览邻居的样本
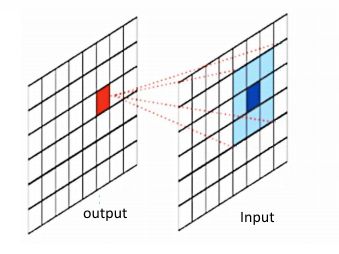
Github Github上的代码This code groups all the neighbors of the image together for each iteration of the For loop. the following illustration will clarify the mechanism of this algorithm.
对于For循环的每次迭代,此代码将图像的所有邻居分组在一起。 下图将阐明该算法的机制。
I have translated this code from the original one written in Matlab(source)
我已经从用Matlab编写的原始代码中翻译了此代码( source )
结论 ( Conclusion)
Experimental studies have shown that the application of LBP can significantly reduce time and computing costs for feature extraction(which will be discussed in future work).
实验研究表明,LBP的应用可以大大减少特征提取的时间和计算成本(将在以后的工作中进行讨论)。
If you find this post useful, feel free to share it, and follow me to tune in for my future posts.
如果您发现此帖子有用,请随时分享,并跟随我收听我将来的帖子。
Finally, You can check out the code on my repo.
最后,您可以在我的repo上签出代码。
Moral: “If you don't know enough, you may be beaten by the ignorant!”
道德:“如果您不够了解,您可能会被无知所殴打!”
Peace ✋
和平✋
翻译自: https://medium.com/swlh/local-binary-pattern-algorithm-the-math-behind-it-️-edf7b0e1c8b3
二进制算法