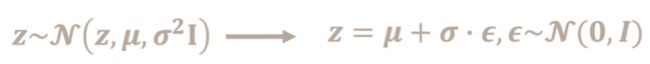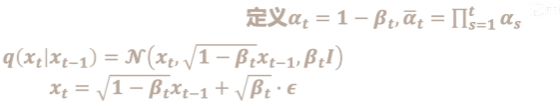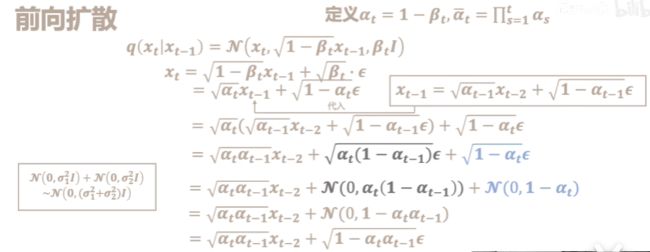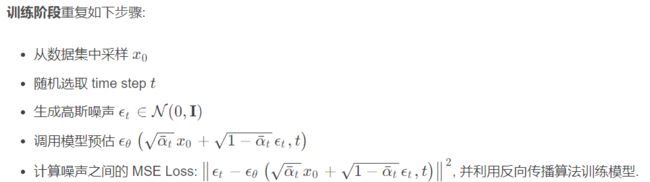生成模型的发展,扩散模型的原理,stable diffusion的实现
文章目录
- 图像生成模型前期发展
- 扩散模型发展
-
- DDPM
-
- 实现细节
- 代码抽象
-
- 重参数技巧
- 前向过程
- 反向过程
- 损失函数
- 总结
- improved DDPM
- diffusion beats GAN
- GLIDE
- DALL·E 2
-
- 框架
- prior模型-diffusion prior
- 后续发展
- **Imagen**
- stable diffusion
- 动机
- 技术实现
-
- 核心技术:Latent Diffusion
- **框架**
- 感知压缩--隐空间
- 语义压缩
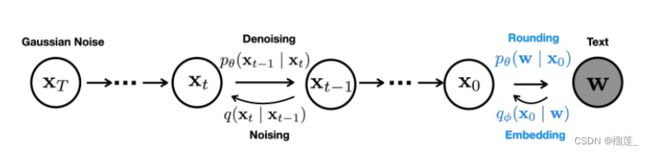
- stable diffusion文字生成图片过程
- 反向扩散过程
-
- 反向扩散细节:单轮去噪U-Net引入多头Attention(改进U-Net结构)
- 扩散损失
- 名词解释
-
- 贝叶斯法则
- 什么是高斯噪声
- 各向同性的高斯分布
- 变分贝叶斯
- 期望
- 边缘概率分布
- 参数重整化
- 扩散过程推导过程
-
- 扩散过程
- 逆过程
图像生成模型前期发展
GAN:左右手互博,对抗学习。两个网络:生成器和判别器。生成器生成图片,判别器判别这是假的图片,互相提高。保真度非常高。
最致命缺点:训练不够稳定。图像多样性不好(创造性不好)。是一个网络隐式的生成,不是概率模型。
Auto-Enocoder:自己重建自己
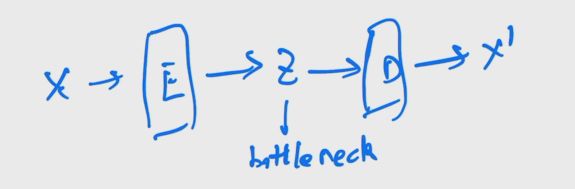
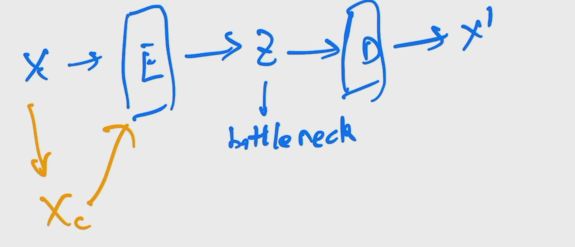
DAE:后续又出现了denoising auto encoder(DAE),简单来说就是对原图的一个打乱,把经过扰乱后的输入 x ′ x' x′传入编码器.后续和Auto-Enocoder一样重建原始 x x x,这个改进会使得视觉训练出来的更吻合.后面MAE也同理.DAE最终目的还是去学习中间的bottleneck,然后把bottleneck做一些分类检测目标分割任务,并不是做生成的.缺点是由于学到的是特征而不是概率分布,没法进行采样.但是encoder-decoder结构值得借鉴.
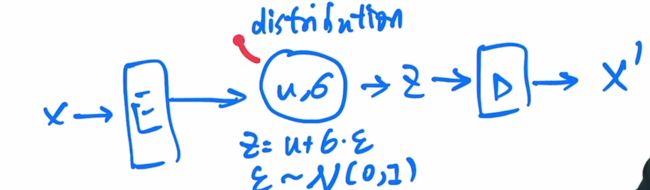
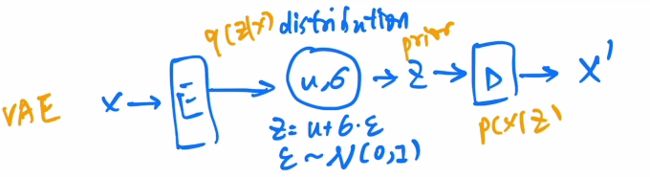
VAE:中间不是学习bottleneck特征,而是一个高斯分布,就可以通过特征和方差进行描述.用fc层预测均值和方差,然后使用公式$z = u+\sigma e $采样一个z,经过解码器就可以生成照片了.
前面部分是后验概率,后面部分是先验分布.最终目的是maximizing likelihood.而且从分布中抽样的多样性也会增加.
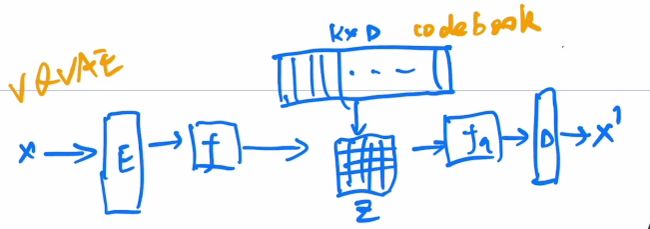
VQ-VAE:(VQ:vector context目的是把VAE做量化).现实生活中需要把连续的任务离散化,把回归任务变成分类任务,所以需要把VAE做大,因此用codebook进行表示,形成VQ-VAE.这个codebook可以看成聚类中心,大小一般是8192x768.从 f f f输出得到的特征图向量到codebook里面做对比看谁最接近 ,然后把最接近的聚类中心放到Z里面(Z里面存的是编号).根据Z的存储生成新的特征图,然后优化起来就比较容易(因为范围固定).
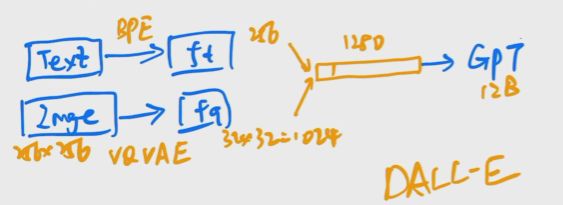
DALL-E:把VQ-VAE结合GPT通过自回归的方式生成图片.
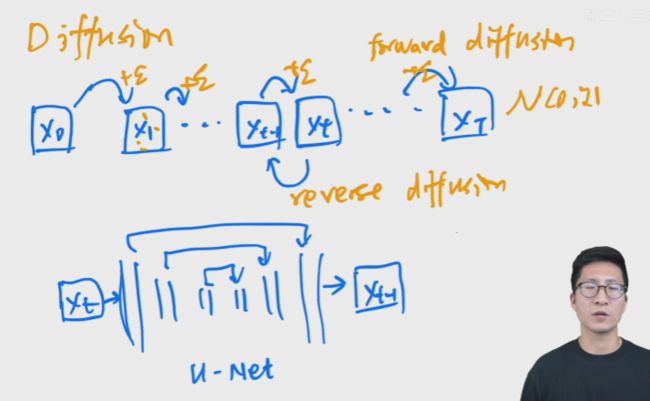
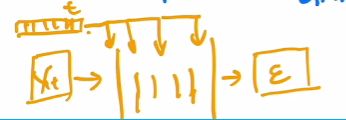
Diffusion model:forward diffusion是每一步都加入正态分布的噪声.最终获得一个各向同性的正态分布(真正的噪声).reverse diffusion:使用unet.(扩散模型的缺点是生成时间太长了,推理速度太慢.)
ps:每一步使用unet进行 x t x_t xt到 x t − 1 x_{t-1} xt−1的推理,unet在每个阶段是共享参数的.
扩散模型发展
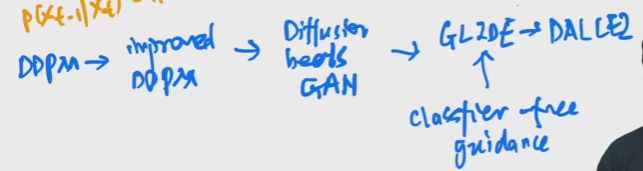
之前的工作的缺点是保真度比不过GAN,因为扩散模型是一个概率分布模型,在分布中抽样保持多样性。后续的一系列工作DDPM,Improved DDPM,Diffusion Models Beat GANs,一直到最新的GLIDE。其中有一个技巧是叫做guidance technique牺牲一部分多样性达到保真性。
DDPM
前提条件:1.马尔可夫过程。2.微小噪声变化。
在DDPM中我们基于初始图像状态以及最终高斯噪声状态,通过贝叶斯公式以及多元高斯分布的散度公式,可以计算出每一步骤的逆向分布。之后继续重复上述对逆向分布的求解步骤,最终实现从纯高斯噪声,恢复到原始图片的步骤。
模型优化部分通过最小化分布的交叉熵,预测出模型逆向分布的均值和方差,将其带入步骤一中的推理过程即可。
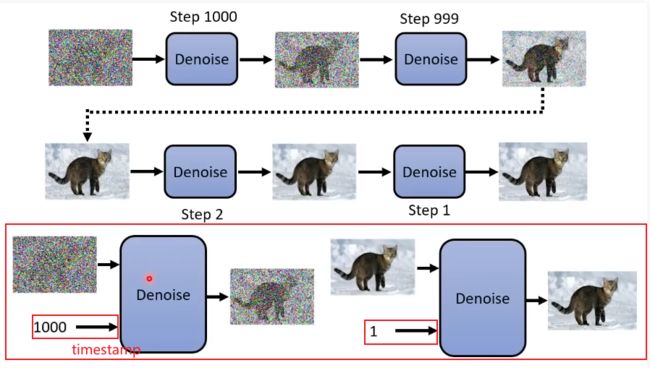
DDPM主要贡献:1.从预测转换图像改进为预测噪声(噪声预测出来后, x t − x_t- xt−噪声= x t − 1 x_{t-1} xt−1)。
Diffusion Model (扩散模型) 是一类生成模型, 和 VAE (Variational Autoencoder, 变分自动编码器), GAN (Generative Adversarial Network, 生成对抗网络) 等生成网络不同的是, 扩散模型在前向阶段对图像逐步施加噪声, 直至图像被破坏变成完全的高斯噪声, 然后在逆向阶段学习从高斯噪声还原为原始图像的过程.
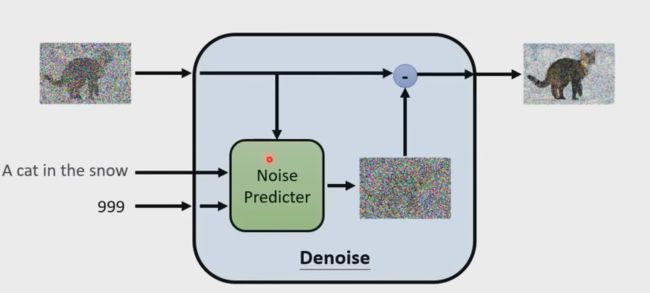
解决了推理步骤过长的问题,将通过Unet预测图片改成预测添加的噪声从而减少运算.t是一个timestamp embedding,告诉unet现在是反向过程的第几步,这个相当于transformer的位置编码.这个做法对整个图像的生成和采样都很有帮助.
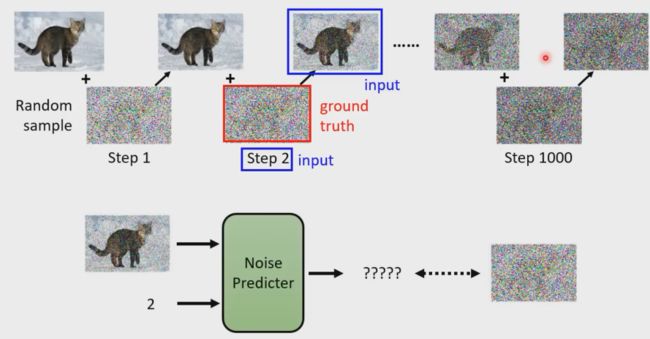
所以损失函数就是对预测噪声和前向过程的ground-truth逼近就行.
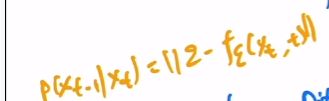
DDPM做出的第二个贡献:在预测过程中只需要预测均值即可,因为方差只要是一个常数值就已经效果很好了.
DDPM和VAE有很多相似之处,DDPM也可以看作一个Encoder-Decoder的结构模型,不过与VAE相比,DDPM的forward diffusion过程模型是固定的,并且整个过程中维度是不变化的.
实现细节
参考:https://www.bilibili.com/video/BV1PY411Z74Z/?spm_id_from=333.337.search-card.all.click&vd_source=68d178d902f684eaf83247c083d8c279
https://blog.csdn.net/Eric_1993/article/details/127455977
https://zhuanlan.zhihu.com/p/599887666
https://mp.weixin.qq.com/s/Xyg00v3KueCgEc1nrKIuyw
https://blog.csdn.net/Eric_1993/article/details/127455977
代码抽象
https://zhuanlan.zhihu.com/p/577778277
重参数技巧
![]()
前向过程
- 1/添加噪声:函数q是用来给输入数据添加噪声
其中 β t \beta_t βt是随着时间增长不断变大的.

反向过程
Denoise的实现细节
ground-truth
怎么把文字加入进来
损失函数
![]()
总结
- 前向加噪的过程中,噪声遵循高斯分布,可以从 x 0 x_0 x0很容易就推到到 x t x_t xt,这个噪声从0.0001逐步增加到0.02。进一步可以直接推导出一个公式计算出任一步加噪过程的图片结果。
- 反向去噪过程中,根据 x t x_t xt反向去噪还原成 x 0 x_0 x0是无法直接通过上面的推导的公式计算的,因为噪声是从正态分布中随机生成的,因此提出使用U-net模拟出噪声的均值和方差,再根据重参数化技巧获得噪声。
- 优化目标:虽然没法直接求出每阶段的噪声分布 p θ ( x t ) p_\theta(x_t) pθ(xt),但是我们是知道先验分布 p θ ( x t ∣ x t − 1 ) p_\theta(x_{t}|x_{t-1}) pθ(xt∣xt−1)和后验分布的,结合贝叶斯公式和ELBO和KL散度,进一步最小化「噪声估计模型 ϵ θ ( x t , t ) ϵ_θ(x_t,t) ϵθ(xt,t)估计的噪声」与「真实噪声」之间的差距。
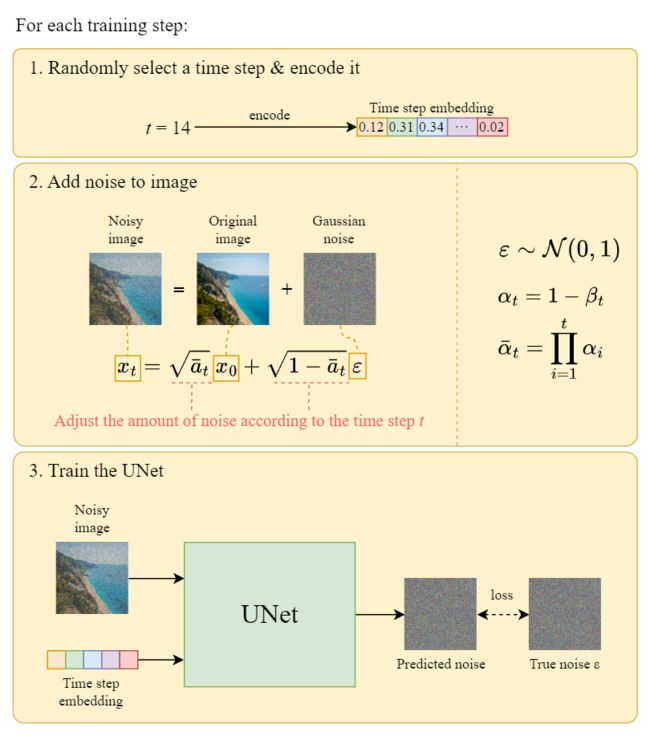
加噪的过程如下
然后反向推导的过程如下
整个训练过程
![]()
improved DDPM
20年底放到Arxiv.进行了方差的学习,把噪声的schedule从一个线性的变成余弦的,然后使用了大模型生成了更好的生成结果
diffusion beats GAN
把模型加大加宽,加注意力头的数量,提出了新的归一化方式,通过步数归一化.还使用了classifier guidance的方法加速了图像生成.即在训练过程中训练一个分类器(为了提高图像预测的准确性).
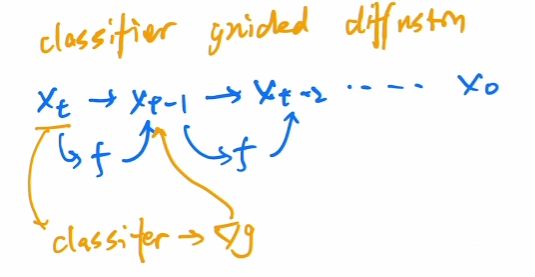
然后有人思考是否不只是用梯度控制图像的采样和生成,而是通过文本/图像/特征等控制采样和生成.但是这个成本很高且不可控
GLIDE
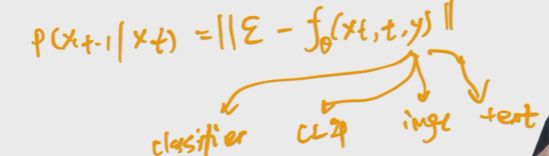
使用classifier free guidance.找到别的指导信号.y是有条件时的输出,空集是无条件时的输出,进行逼近.
DALL·E 2
Hierarchical Text-ConditionalImage Generation with CLIP Latents
优势:DALL·E 2并不是一对一的映射,让艺术的创造触手可及。输入文本,能够生成一个自创的图片,并且能够考虑图片的纹理等信息以及指定不同的位置生成,还有考虑指定物体在图片上生成的合理性。还能给定已有图片,去生成很多类似的图片风格。
和DALL·E 1相比分辨率也更高了。
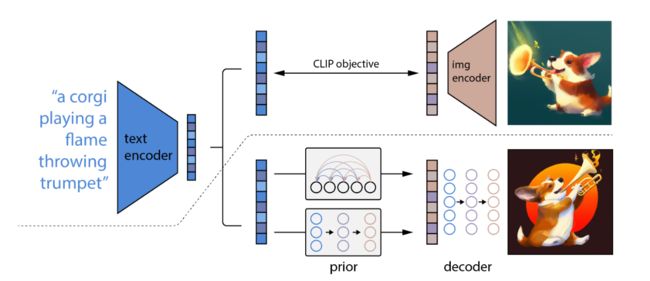
框架
生成方式:整个过程就是给定一个文本从clip(模型固定)输出对应的图像特征作为ground truth,然后经过prior通过文本生成另外图像特征(增加图像的diversity),然后。使用层级式的方法生成高分辨率的图像,比如从64x64上采样到256x256再上采样到1024x1024.使用clip中提取文本,然后生成新的图像。
模型:本质上是CLIP模型+GLIDE模型(基于扩散模型的文本图像生成方法)。模型训练是两个阶段:prior和decoder。
为什么两阶段
prior模型-diffusion prior
过程中使用了classifier-free guidance.还训练了一个decoder-only transformer,因为方便处理prior输出的序列问题.优化目标是预测输出与clip输出的均方误差.
![]()
后续发展
Imagen
stable diffusion
参考链接
网址:https://stablediffusionweb.com/#demo
GitHub:https://github.com/CompVis/stable-diffusion
diffusion用于生成模型的发展过程Latent Diffusion Models->stable diffusion做了哪些改进和提升
主要参考文章:https://zhuanlan.zhihu.com/p/600251419
核心代码讲解十分清晰:https://zhuanlan.zhihu.com/p/613337342
动机
对于带有噪声的图,通过迭代的生成噪声片段来一步一步消除噪声 比 直接在原图上去除噪声要好(扩散模型的马尔可夫过程).但扩散模型的最大问题在于对算力要求极高,所以Stable Diffusion使用Latant Diffusion模型不直接操作图像,而是在潜在空间中进行操作,将原始数据编码到更小空间,让U-Net可以在低纬表示上添加和删除噪声.
技术实现
核心技术:Latent Diffusion
概念:潜在空间简单的说是对压缩数据的表示。通过降维我们可以过滤掉一些不太重要的信息你,只保留最重要的信息。因此,空间变小,以便提取和保留最重要的属性。这就是潜在空间适用于扩散模型的原因。
作用:将GAN的感知能力、扩散模型的细节保存能力和Transformer的语义能力三者结合.与其他方法相比,Latent Diffusion不仅节省了内存,而且生成的图像保持了多样性和高细节度,同时图像还保留了数据的语义结构。
阶段:任何生成性学习方法都有两个主要阶段:感知压缩和语义压缩。
框架
感知压缩–隐空间
在感知压缩学习阶段,学习方法必须去除高频细节将数据封装到抽象表示中。用自动编码器 (Auto Encoder) 结构捕获感知压缩。自动编码器中的编码器将高维数据投影到潜在空间,解码器从潜在空间恢复图像。
损失函数:该损失函数确保重建限制在图像流形内,并减少使用像素空间损失(例如 L1/L2 损失)时出现的模糊。
语义压缩
图像生成方法必须捕捉到数据中的语义结构.这种概念和语义结构提供了图像中各种对象的上下文和相互关系的保存。Transformer擅长捕捉文本和图像中的语义结构。Transformer的泛化能力和扩散模型的细节保存能力相结合,提供了两全其美的方法,并提供了一种生成细粒度的高度细节图像的方法,同时保留图像中的语义结构。
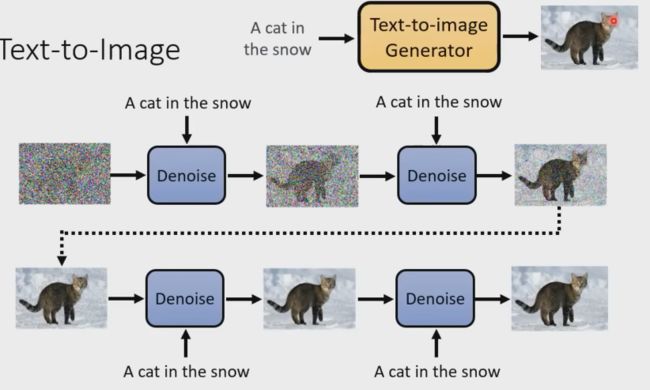
stable diffusion文字生成图片过程
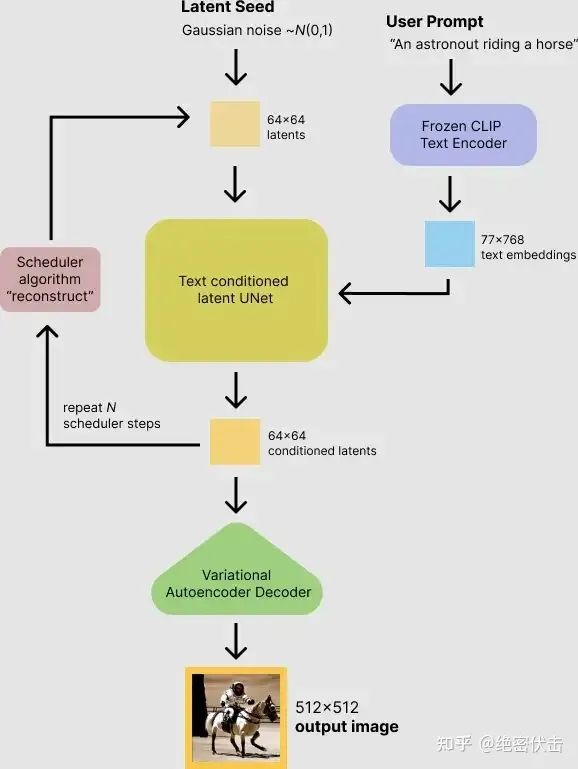
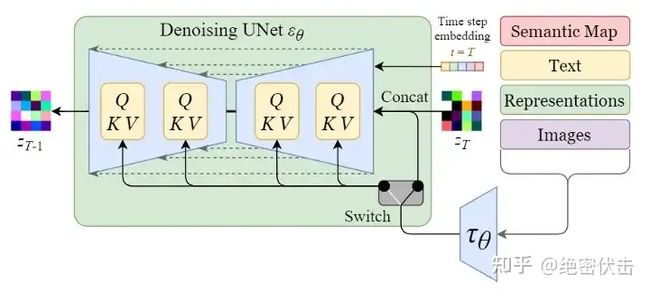
可以看到,对于输入的文字(图中的“An astronout riding a horse”)会经过一个CLIP模型转化为text embedding,然后和初始图像(初始化使用随机高斯噪声Gaussian Noise)一起输入去噪模块(也就是图中Text conditioned latent U-Net),最后输出 512×512 大小的图片。在文章(绝密伏击:十分钟读懂Diffusion:图解Diffusion扩散模型)中,我们已经知道了CLIP模型和U-Net模型的大致原理,这里面关键是Text conditioned latent U-net,翻译过来就是文本条件隐U-net网络,其实是通过对U-Net引入多头Attention机制,使得输入文本和图像相关联
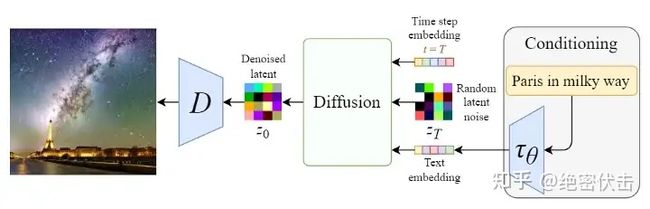
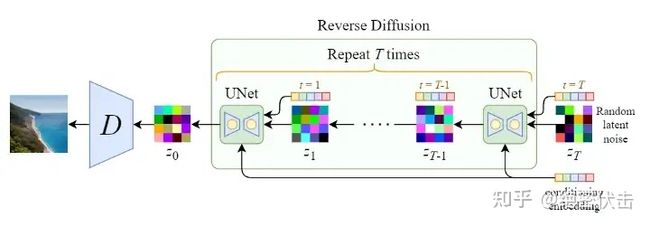
反向扩散过程
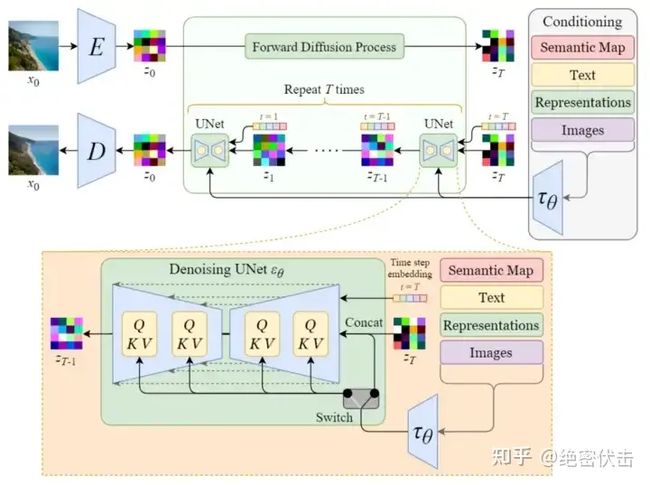
反向扩散细节:单轮去噪U-Net引入多头Attention(改进U-Net结构)
上图的最左边里面的Semantic Map、Text、Representations、Images稍微不好理解,这是Stable Diffusion处理不同任务的通用框架:
- Semantic Map:表示处理的是通过语义生成图像的任务
- Text:表示的就是文字生成图像的任务
- Representations:表示的是通过语言描述生成图像
- Images:表示的是根据图像生成图像
这里我们只考虑输入是Text,因此首先会通过模型CLIP模型生成文本向量,然后输入到U-Net网络中的多头Attention(Q, K, V)。
这里补充一下多头Attention(Q, K, V)是怎么工作的,我们就以右边的第一个Attention(Q, K, V)为例。
扩散损失
条件扩散:扩散模型是依赖于先验的条件模型。在图像生成任务中,先验通常是文本、图像或语义图。为了获得先验的潜在表示,需要使用转换器(例如 CLIP)将文本/图像嵌入到潜在向量中。因此,最终的损失函数不仅取决于原始图像的潜在空间,还取决于条件的潜在嵌入。
注意力机制:使用交叉注意力机制将CLIP这种潜在嵌入和Z这个隐空间表达进行结合.
名词解释
贝叶斯法则
在贝叶斯法则中,每个名词都有约定俗成的名称:
- Pr(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
- Pr(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
- Pr(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
- Pr(B)是B的先验概率或边缘概率,也作标准化常量(normalized constant)。
全事件一般是统计获得的,所以称为先验概率,没有实验前的概率。新事件一般是实验,如试验B,此时的事件背景从全事件变成了B,该事件B可能对A的概率有影响,那么需要对A现在的概率进行一个修正,从P(A|Ω)变成 P(A|B),所以称 P(A|B)为后验概率,也就是试验(事件B发生)后的概率
有条件概率的都可以被称之为后验概率。按这些术语,Bayes法则可表述为:后验概率 = (似然度 * 先验概率)/标准化常量
也就是说,后验概率与先验概率和似然度的乘积成正比。另外,比例Pr(B|A)/Pr(B)也有时被称作标准似然度(standardised likelihood),Bayes法则可表述为:后验概率 = 标准似然度 * 先验概率。
什么是高斯噪声
https://www.zgbk.com/ecph/words?SiteID=1&ID=113493&SubID=101453

各向同性的高斯分布
各向同性的高斯分布(球形高斯分布)指的是各个方向方差都一样的多维高斯分布,协方差为正实数与identity matrix相乘。
因为高斯的circular symmetry,只需要让每个轴上的长度一样就能得到各向同性,也就是说分布密度值仅跟点到均值距离相关,而不和方向有关。
各向同性的高斯每个维度之间也是互相独立的,因此密度方程可以写成几个1维度高斯乘积形式。要注意的是,几个高斯分布乘在一起得到各向同性,但几个Laplace分布相乘就得不到各向同性!
此类高斯分布的参数个数随维度成线性增加,只有均值在增加,而方差是一个标量,因此对计算和存储量的要求不大,因此非常讨人喜欢。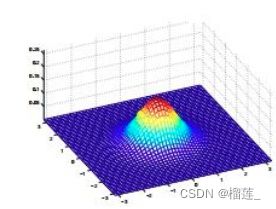
变分贝叶斯
同时对分布Q ( z ) 求期望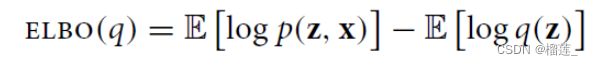
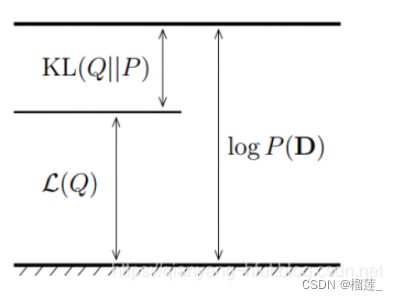
在使用变分推断时,首先需要计算的便是ELBO。从上面的公式可以看到,要计算ELBO,需要写出联合概率密度p (z, x) 和q (z) 。
期望
在概率论和统计学中,一个离散性随机变量的期望值(或数学期望,亦简称期望,物理学中称为期待值)是试验中每次可能的结果乘以其结果概率的总和。换句话说,期望值像是随机试验在同样的机会下重复多次,所有那些可能状态平均的结果,便基本上等同“期望值”所期望的数。期望值可能与每一个结果都不相等。换句话说,期望值是该变量输出值的加权平均。期望值并不一定包含于其分布值域,也并不一定等于值域平均值。
如果 X {\displaystyle X} X是在概率空间 ( Ω , F , P ) ( Ω , F , P ) {\displaystyle (\Omega ,F,P)}{\displaystyle (\Omega ,F,P)} (Ω,F,P)(Ω,F,P)中的随机变量,那么它的期望值 E ( X ) {\displaystyle \operatorname {E} (X)} E(X)的定义是:
E ( X ) = ∫ Ω X d P E ( X ) = ∫ Ω X d P {\displaystyle \operatorname {E} (X)=\int _{\Omega }X\,\mathrm {d} P}{\displaystyle \operatorname {E} (X)=\int _{\Omega }X\,\mathrm {d} P} E(X)=∫ΩXdPE(X)=∫ΩXdP
并不是每一个随机变量都有期望值的,因为有的时候上述积分不存在。
如果两个随机变量的分布相同,则它们的期望值也相同。
如果 X {\displaystyle X} X是离散的随机变量,输出值为 x 1 , x 2 , … x 1 , x 2 , … {\displaystyle x_{1},x_{2},\ldots }x_{1},x_{2},\ldots x1,x2,…x1,x2,… ,和输出值相应的概率为 p 1 , p 2 , … p 1 , p 2 , … {\displaystyle p_{1},p_{2},\ldots }p_{1},p_{2},\ldots p1,p2,…p1,p2,… (概率和为1)。
若级数 ∑ i p i x i ∑ i p i x i {\displaystyle \sum _{i}p_{i}x_{i}}{\displaystyle \sum _{i}p_{i}x_{i}} i∑pixii∑pixi绝对收敛,那么期望值 E ( X ) E ( X ) {\displaystyle \operatorname {E} (X)}{\displaystyle \operatorname {E} (X)} E(X)E(X)是一个无限数列的和。
E ( X ) = ∑ i p i x i E ( X ) = ∑ i p i x i {\displaystyle \operatorname {E} (X)=\sum _{i}p_{i}x_{i}}{\displaystyle \operatorname {E} (X)=\sum _{i}p_{i}x_{i}} E(X)=i∑pixiE(X)=i∑pixi
上面赌博的例子就是用这种方法求出期望值的。如果 X {\displaystyle X} X是连续的随机变量,存在一个相应的概率密度函数 f ( x ) f ( x ) {\displaystyle f(x)}f(x) f(x)f(x),若积分 ∫ − ∞ ∞ x f ( x ) d x ∫ − ∞ ∞ x f ( x ) d x {\displaystyle \int _{-\infty }^{\infty }xf(x)\,\mathrm {d} x}{\displaystyle \int _{-\infty }^{\infty }xf(x)\,\mathrm {d} x} ∫−∞∞xf(x)dx∫−∞∞xf(x)dx绝对收敛,那么 X {\displaystyle X} X的期望值可以计算为:
E ( X ) = ∫ − ∞ ∞ x f ( x ) d x E ( X ) = ∫ − ∞ ∞ x f ( x ) d x {\displaystyle \operatorname {E} (X)=\int _{-\infty }^{\infty }xf(x)\,\mathrm {d} x}{\displaystyle \operatorname {E} (X)=\int _{-\infty }^{\infty }xf(x)\,\mathrm {d} x} E(X)=∫−∞∞xf(x)dxE(X)=∫−∞∞xf(x)dx。
是针对于连续的随机变量的,与离散随机变量的期望值的算法同出一辙,由于输出值是连续的,所以把求和改成了积分。

在写出这两个式子之后,带入ELBO公式,分别求对数。之后,分别求期望。在期望计算完之后,针对具体的变分参数,求偏导,并令偏导为0,即可得到变分参数的更新公式。
在实际公式推导过程中,关键点就在于如何求期望。其计算期望往往需要用到指数分布族的性质,即可以将期望计算转化成求导计算。具体的细节可以参考:https://qianyang-hfut.blog.csdn.net/article/details/87247363
边缘概率分布
https://zh.m.wikipedia.org/zh-hans/%E8%BE%B9%E7%BC%98%E5%88%86%E5%B8%83
参数重整化
扩散过程推导过程
对于扩散模型而言,加入的噪声符合高斯分布/正态分布: X∼N(μ,σ2)
扩散过程
加入噪音进行扩散的过程:
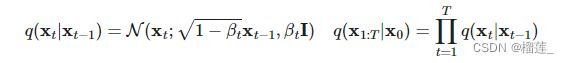
这个条件概率满足正态分布,其中 ( 1 − β t x t − 1 ) \sqrt{(1-\beta_t x_{t-1})} (1−βtxt−1)是均值, β t I \beta_t I βtI是方差。其中 { β t ∈ ( 0 , 1 ) } t = 1 t \{\beta_t \in (0,1)\}_{t=1}^t {βt∈(0,1)}t=1t,这个是在每个阶段自己设置的,可以像学习率一样设置,不过这个是逐渐升高的值(学习率是逐渐减小)
![]()
那么怎么算出 x t x_t xt呢?使用参数重整化技巧,因为 x t x_t xt符合上面公式的分布,那么在正态分布中生成一个 z z z,然后按照下式
x t = a t x t − 1 + 1 − α t z t − 1 x_t = \sqrt {a_t}x_{t-1} + \sqrt {1- \alpha _t z_{t-1}} xt=atxt−1+1−αtzt−1(这个公式就是上面的那个均值乘以 x t − 1 x_{t-1} xt−1 + 上面的那个标准差(方差取根号)乘以随机生成的正态分布的随机量 这就是重整化技巧)
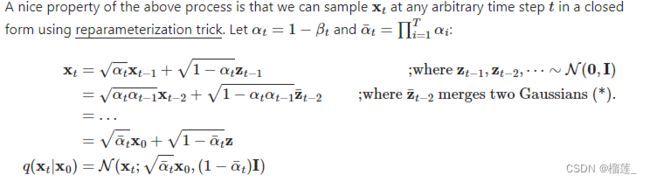
所以扩散过程是一个不含参的分布.扩散过程是对原始图像一步一步加噪,使得图像变成一个高斯分布.但是我们是希望让模型有预测功能.

逆过程
逆过程是从高斯噪声中恢复原始数据,可以假设它是一个高斯分布,但是无法逐步拟合分布,所以需要构建一个参数分布来做估计.逆扩散过程仍然是一个马尔科夫链过程.

AI绘画与CV多模态能力的起源:从VAE、扩散模型DDPM、DETR到ViT/MAE/Swin transformer
CV多模态和AIGC的原理解析:从CLIP、BLIP到Stable Diffusion、Midjourney