数据结构

目录

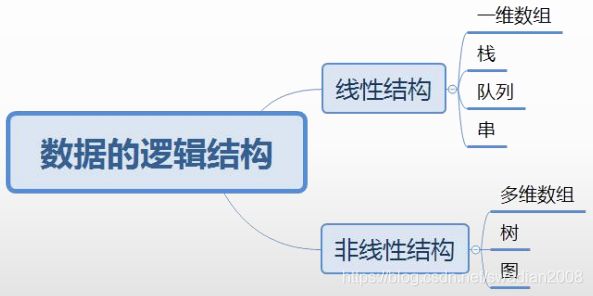
一、数据的线性结构

1、线性表

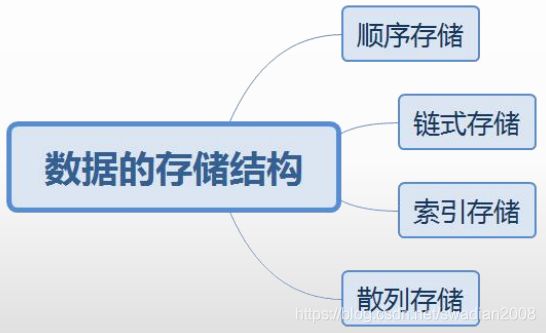
（1）顺序存储

（2）链式存储

（3）单链表和单向循环链表

（4）双向链表和双向循环链表

2、栈

（1）顺序存储

（2）栈的链式存储

3、队列

（1）顺序存储

（2）循环队列

（3）链接存储

（4）双端队列

4、串

二、数据的非线性结构

1、二维数组和特殊矩阵

2、树

3、二叉树

4、二叉树的遍历

5、二叉树的存储

（1）顺序存储

（2）链式存储

6、二叉查找树

7、哈夫曼树

8、图

（1）无向完全图和有向完全图

（2）连通图和强连通图

（3）图的存储——邻接矩阵和邻接表

（4）图的遍历

---

一、数据的线性结构

1、线性表

（1）顺序存储

用一组地址连续的存储单元依次存储线性表中的数据元素，从而使得逻辑上相邻的元素在物理位置上也相邻。

优点：随机存取表中的元素。

缺点：插入和删除操作需要移动元素。

移动元素的期望值：插入元素n/2个；删除元素（n-1）/2个  （// TODO需要解释）

（2）链式存储

线性表的链式存储是用通过指针链接起来的结点来存储数据元素。

存储各数据元素的结点的地址并不要求是连续的，因此存储数据元素的同时必须存储元素之间的逻辑关系。另外，结点空间只有在需要的时候才申请，无须事先分配。

（3）单链表和单向循环链表

单链表只能从头结点开始往后顺序遍历整个链表。

循环单链表可以从表中的任一结点开始遍历整个链表。

单链表

单项循环链表

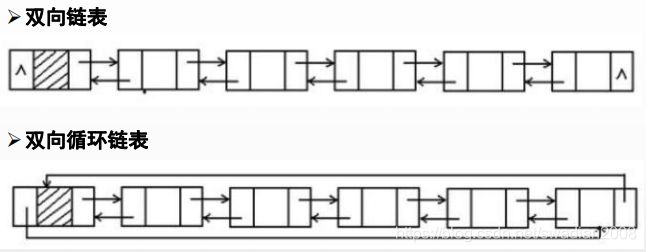
（4）双向链表和双向循环链表

典型真题一

若对线性表的最常用操作是访问任意指定序号的元素，并在表尾加入和删除元素，则适宜采用（ ）存储。

• A．顺序表
• B．单链表
• C．双向链表
• D．哈希表

试题分析

采用顺序表(即数组)，可以任意访问指定序号的元素，便于在表尾加入和删除元素，但不便于在表头插入和删除元素，在表头操作时需要移动大量元素。

要注意的是，题目中要求在表尾加入和删除元素，而不是在表头操作，因此适宜采用顺序表。

采用链表插入、删除元素较为方便，但是访问指定序号的元素较为麻烦，需要从头指针开始遍历。

参考答案：A

典型真题二

设有一个包含n个元素的有序线性表。在等概率情况下删除其中的一个元素，若采用顺序存储结构，则平均需要移动（）个元素；若采用单链表存储，则平均需要移动（）个元素。

• A．1                  B．(n-1)/2                  C．Log2n                      D．n
• A．0                   B．1                          C．(n-1)/2                      D．n/2

参考答案：B、A

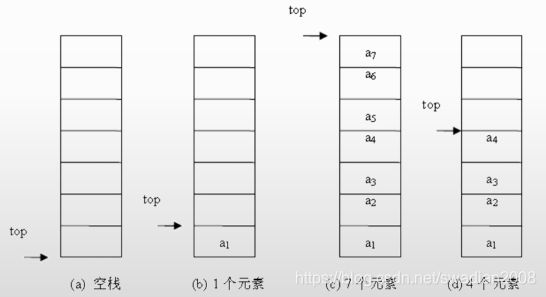
2、栈

（1）顺序存储

预先申请栈空间，栈满则元素不能入栈。

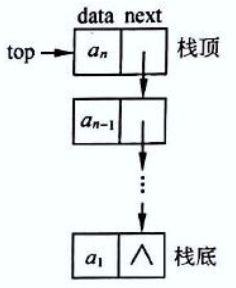
（2）栈的链式存储

用链表表示栈，用链表实现的栈称为链栈。由于栈中元素的插入和删除仅在栈顶一端进行，因此不必另外设置头指针，链表的头指针就是栈顶指针。

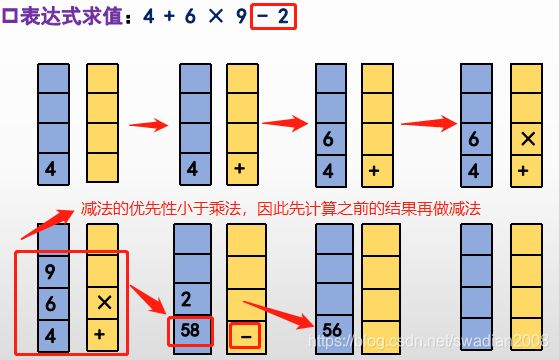
应用：表达式求值过程

典型真题一

栈的特点是后进先出，若用单链表作为栈的存储结构，并用头指针作为栈顶指针，则（ ）。

• A.入栈和出栈操作都不需要遍历链表
• B.入栈和出栈操作都需要遍历链表
• C.入栈操作需要遍历链表而出栈操作不需要
• D.入栈操作不需要遍历链表而出栈操作需要

试题解析：

本题用单链表作为栈的存储结构，因为栈的操作是先进后出，因此无论是入栈还是出栈，都只对栈顶元素操作，而在单链表中用头指针作为栈顶指针，此时无论是出栈还是入栈，都只需要对头指针指向的栈顶指针操作即可，不需要遍历链表。

参考答案：A

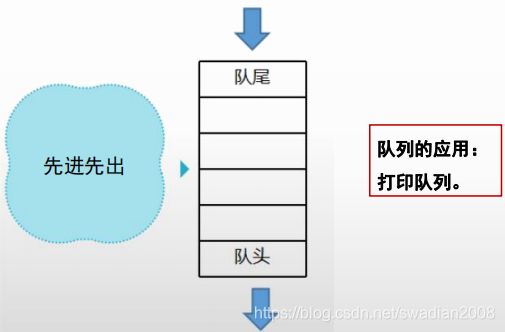
3、队列

（1）顺序存储

队列的顺序存储结构又称为顺序队列，它也是利用一组地址连续的 存储单元存放队列中的元素。

由于队列中元素的插入和删除限定在表的两端进行，因此设置队头指针和队尾指针，分别指出当前的队头和队尾。

典型真题一

对于一个长度为n(n＞1)且元素互异的序列，令其所有元素依次通过一个初始为空的栈后，再通过一个初始为空的队列。假设队列和栈的容量都足够大，且只要栈非空就可以进行出栈操作，只要队列非空就可以进行出队操作，那么以下叙述中，正确的是（ ）。

• A出队序列和出栈序列一定互为逆序
• B出队序列和出栈序列一定相同
• C入栈序列与入队序列一定相同
• D入栈序列与入队序列一定互为逆序

试题分析_可以举例分析

本题考查数据结构基础知识。

栈和队列都是线性的数据结构。栈的操作要求是入栈和出栈都在表尾进行，即在栈中有多个元素时，后进去的元素先出来，特点是后进先出，元素入栈的顺序与出栈的顺序可以相同也可以不同。而队列的修改要求是在队尾加入元素，在队头删除元素，特点是先进先出，元素的入队顺序与出队顺序一定相同。将一个栈和队列连接后，进出队列的元素顺序是相同的，而进入队列的元素顺序正是从栈中出来的元素顺序，因此，正确的叙述为出队序列与出栈序列一定相同。

参考答案：B

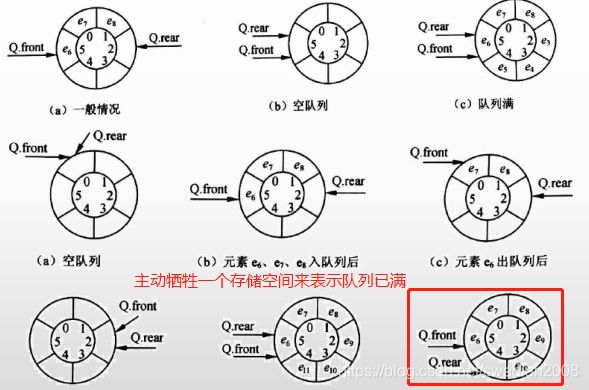
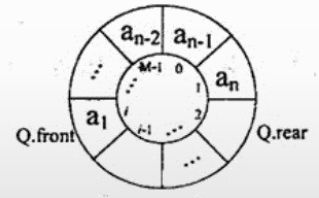
（2）循环队列

典型真题

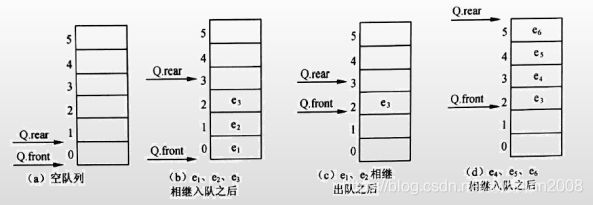
设某循环队列Q的定义中有front和rear两个域变量，其中，front指示队头元素的位置，rear指示队尾元素之后的位置，如下图所示。若该队列的容量为M，则其长度为（）。

• A (Q.rear-Q.front +1)                             B (Q.rear-Q.front+M)
• C (Q.rear-Q.front+1)%M                        D (Q.rear-Q.front+M)%M

试题分析

本题考查数据结构基础知识。根据题目中所给的示意图，Q.front为队头元素的指针，Q.rear表示队尾元素之后的一个空位置，故队列长度为Q.rear-Q.front，由于队列中存储位置编号是在0～M－1之间循环的，Q.rear-Q.front的结果有可能是负数，故在Q.rear-Q.front基础上加上M可恢复为正数，而此正数有可能超出0～M－1的范围，故用整除，M取余运算恢复一下，因此长度计算的式子为(Q.rear-Q.front+M)%M。

参考答案：D

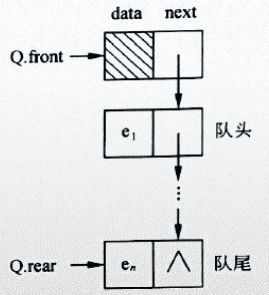
（3）链接存储

用链接存储线性表实现队列，用链表实现的队列称为链接队列。

典型真题

队列的特点是先进先出，若用循环单链表表示队列，则( )。

• A.入队列和出队列操作都不需要遍历链表
• B.入队列和出队列操作都需要遍历链表
• C.入队列操作需要遍历链表而出队列操作不需要
• D.入队列操作不需要遍历链表而出队列操作需要

参考答案：A

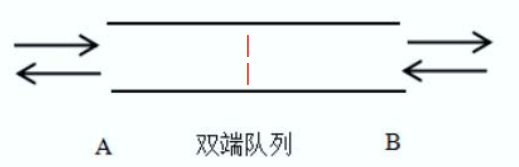
（4）双端队列

某双端队列如下图所示，要求元素进出队列必须在同一端口，即从A端进入的元素必须从A端出、从B端进入的元素必须从B端出。

典型真题

双端队列是指在队列的两个端口都可以加入和删除元素，如下图所示，现在要求元素进队列和出队列必须在同一端口。

即从a端进队的元素必须从a端出，从b端进队的元素必须从b端出。

则对于四个元素的序列a.b.c.d，若要。求前两个元素a.b从a端口按次序全部进入队列。后两个元素Cd从b端口按次序全部进入队列，则不可能得到的出队序列是（ ）。

• A.d、a、b、c               B.d、c、b、a
• C.b、a、d、c               D.b、d、c、a

相当于两个栈

参考答案：A

4、串

串是仅由字符构成的有限序列，是一种线性表。一般记为s= ‘a1a2......an’(n>0)，其中，s是串的名称，用单引号括起来的字符序列是串值。串的基本概念：

1. 空串：长度为零的串称为空串，空串不包含任何字符。
2. 空格串：由一个或多个空格组成的串。
3. 子串：由串中任意长度的连续字符构成的序列称为子串。

含有子串的串称为主串。空串是任意串的子串。

典型真题

设S是一个长度为n的非空字符串，其中的字符各不相同，则其互异的非平凡子串（非空且不同于S本身）个数为 （ ） 。

• A．2n-1                                         B．n²
• C．n(n+1)/2                                  D．(n+2) (n-1)/2

试题分析

任取一个字符串abcd，它的非空子集有：a、b、c、d、ab、bc、cd、abc、bcd共9个。注意：abd、acd、bd、ad等不属于它的子串。

参考答案：D

二、数据的非线性结构

1、二维数组和特殊矩阵

二维数组

特殊矩阵——只考虑这一种

这一种的存储方式也是两种：按行存和按列存

典型真题一

某n阶的三对角矩阵A如下图所示，按行将元素存储在一堆数组M 中，设a1,1存储在M[1]，那么ai，j(1<=i，j<=n且ai，j位于三条对角线中），存储在M（）。

• A.i+2j         B.2i+j       C.i+2j-2        D.2i+j-2

试题分析

本题用带入法，取满足题干要求的i和j的数值，带入四个选项可得选项D是正确答案。使用a1,1存储在M[1]，和a2,1存储在M[2]进行代入计算

参考答案：C

典型真题二

对于一个n阶的对称矩阵A，将其下三角区域（含主对角线）的元素按行存储在一维数组中，设元素A[i][y]存放在S[k]中，且S[1]=A[0][0]，则k与i，y（i<=y）的对应关系是（ ）。

• A.K=i（i+1）/2+y-1     B.k=i（i+1）/2+y+1   
• C.K=i（i-1）/2+y-1      D.k=i（i-1）/2+y-1

试题分析

这道题可以将“S[1]=A[0][0]”这个条件带入四个选项中，

只有选项B符合要求。

参考答案：B

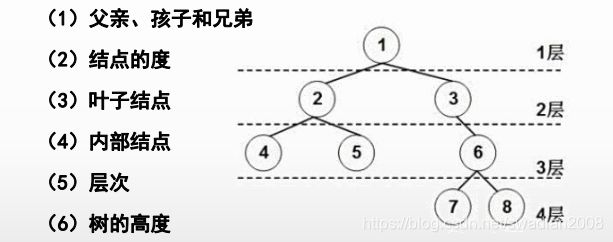
2、树

3、二叉树

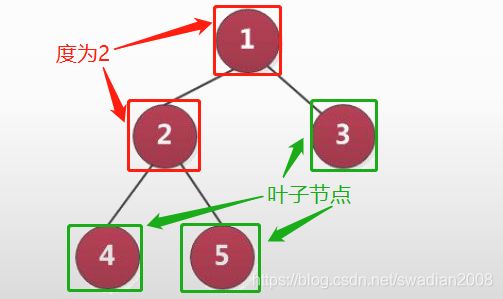
度为2的树——>二叉树，即每个节点最多有两个孩子节点。

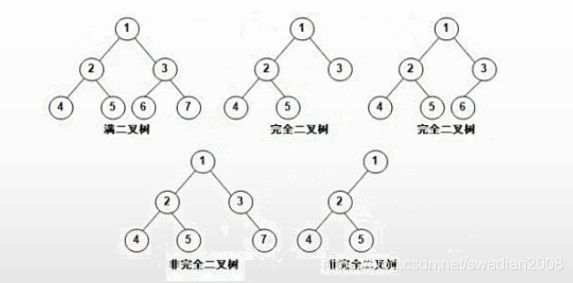
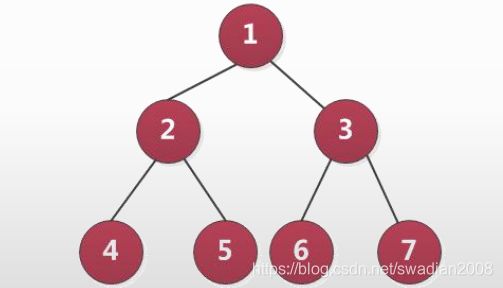
满二叉树：每个节点都有两个分支。

完全二叉树：除了最下边一层，所有上层都是满二叉树，并且最底层元素从左到右排列。

二叉树：

1. 在二叉树的第 i 层上最多有2^(i-1）个结点（i≧1）——>每一层的元素，为2的(n-1)次方个
2. 深度为 k 的二叉树最多有(2^k)-1个结点（k≧1）——>有n层就有2的n次方-1个元素（根节点只有一个）
3. 对于任何一棵二叉树，如果其叶子结点数为N0 ，度为 2 的结点数为N2，则N0=N2+1

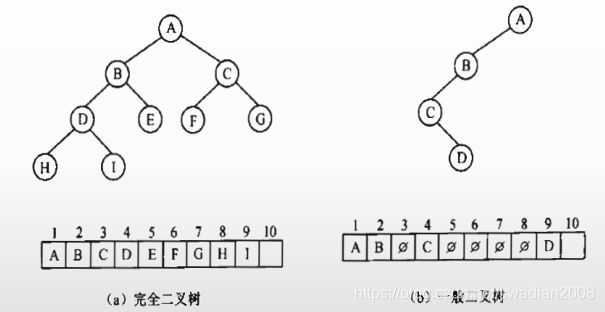
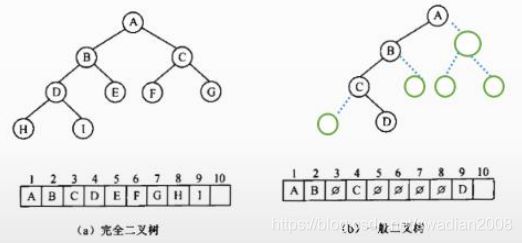
完全二叉树：——使用画图代入法

   ——求二叉树的深度

—— log以2为底n的对数向下取整 + 1 ——>“L”符号为向下取整，倒过来为向上取整

如果i=1(i表示第1个节点)，则结点i无父结点，是二叉树的根；如果i＞1，则，父结点是⌊ i/2⌋ ；

如果2i＞n(节点个数)，则结点i为叶子结点，无左子结点；否则，其左子结点是2i；

如果2i+1＞n，则结点i无右子结点，否则，其右子节点是结点2i+1。

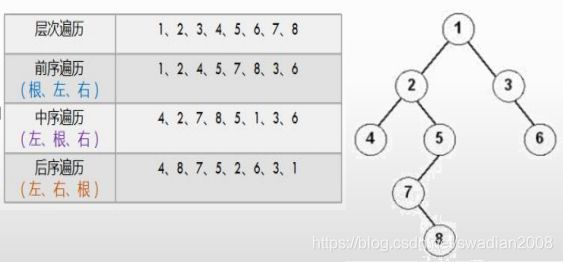
4、二叉树的遍历

二叉树的遍历：是指从根结点出发，按照某种次序依次访问二叉树中所有的结点，使得每个结点被访问一次且仅被访问一次。

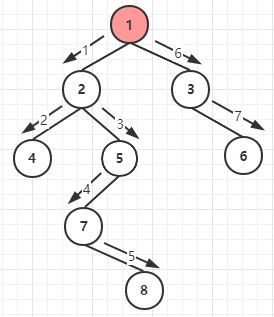
前序遍历——节点在前（中、左、右）

先遍历节点——>然后遍历节点的左子树——>最后遍历节点的右子树

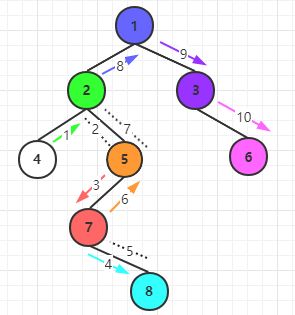
中序遍历——节点在中（左、中、右）

先遍历节点的左子树——>然后遍历节点——>最后遍历节点的右子树

后续遍历——节点在后（左、右、中）

先遍历节点的左子树——>然后遍历节点的右子树——>最后遍历节点

典型真题一

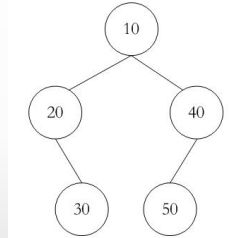
某二叉树的中序，先序遍历序列分别为{20，30，10，50，40}，{10，20，30，40，50}则该二叉树的后序遍历序列为（ ）。

• A.50，40，30，20，10
• B.30，20，10，50，40
• C.30，20，50，40，10
• D.20，30，10，40，50

试题分析

根据要求构造出二叉树。

可以看出后序遍历是 30,20,50,40,10

参考答案：C

典型真题二

已知某二叉树的先序遍历序列为A B C D E F、中序遍历序列为B A D C F E，则可以确定该二叉树（ ）。

• A.是单支树（即非叶子结点都只有一个孩子）
• B.高度为4（即结点分布在4层上）
• C.根结点的左子树为空
• D.根结点的右子树为空

试题解析：

根据先序遍历和中序遍历序列可以构造出二叉树高度为4的所以

选择B

参考答案：B

5、二叉树的存储

（1）顺序存储

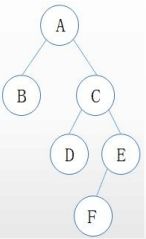
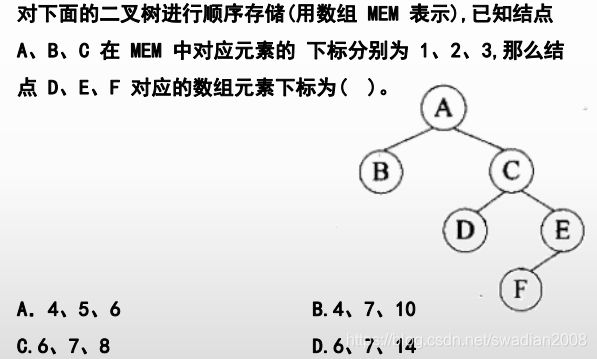
典型真题一

试题分析

为题干中B的子树构造一些虚拟的结点，所以 D、E、F 对应的数组元素下标为6、7、14。

参考答案：D

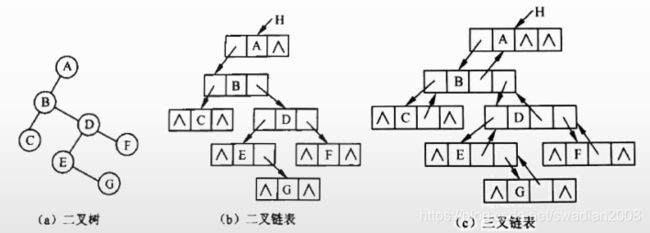
（2）链式存储

典型真题

设某二叉树采用二叉链表表示（即结点的两个指针分别指示左、右孩子）。当该二叉树包含 k 个节点时，其二叉链表节点中必有（）个空的孩子指针。

• A．k-1
• B．K
• C．k+1
• D．2k

试题分析

二叉链表中每个结点有2个指针，一共有2K个指针。在二叉树中除了根结点之外，其他的结点都有一条边进入该结点，即一个指针指向该结点，所以二叉树中边的总个数为k-1，也就说 明非空指针的个数为k-1个。那么空指针的个数为：总的结点数-非空指针的个数=2k-（k-1）=k+1。

参考答案：C

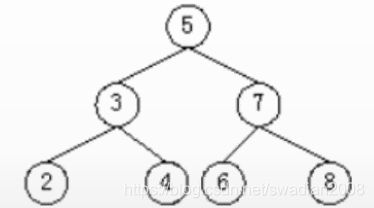
6、二叉查找树

二叉排序树又称为二叉查找树，其定义为二叉排序树或者是一棵空二叉树，或者是具有如下性质的二叉树：

（1）若它的左子树非空，则左子树上所有结点的值均小于根结点。

（2）若它的右子树非空，则右子树上所有结点的值均大于根结点。

（3）左、右子树本身又各是一棵二叉排序树。

如果中序遍历二叉排序树，就能得到一个排好序的结点序列。

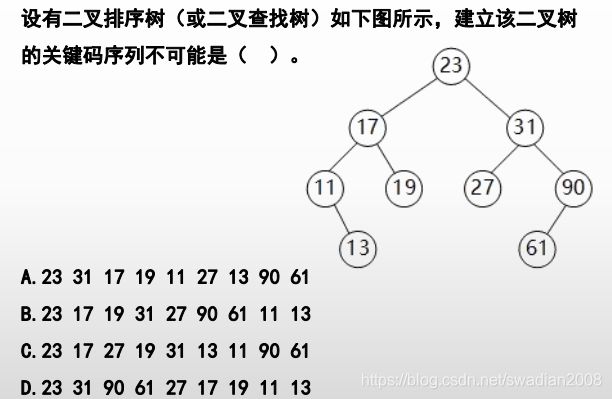
典型真题

试题分析

注意27在31的后面可以得到答案C

试题答案：C

7、哈夫曼树

哈夫曼编码——>压缩文件

一定条件下，寻找目标数据，为了减少判断次数，选取合适的根节点

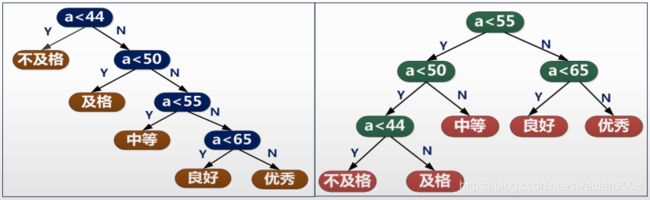
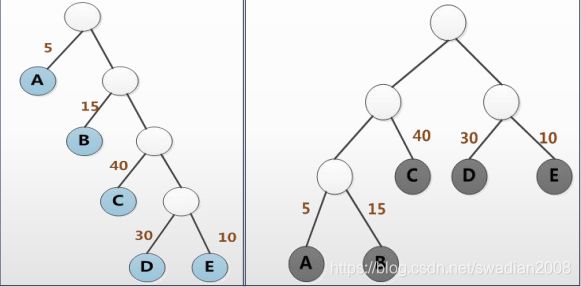
设置：A不及格、B及格、C中等、D良好、E优秀，根据数据占比和深度计算带权长度

带权路径长度WPL1=1×5+2×15+3×40+4×30+4×10=315

带权路径长度WPL2=3×5+3×15+2×40+2×30+2×10=220

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(HuffmanTree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

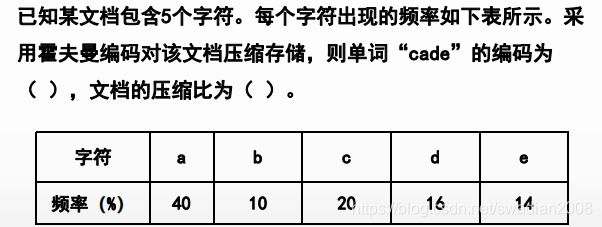
典型真题

• A.1110110101          B.1100111101
• C.1110110100          D.1100111100
• A.20%                      B.25%
• C.27%                      D.30%

试题分析

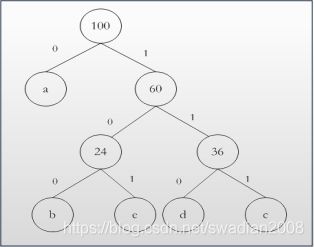
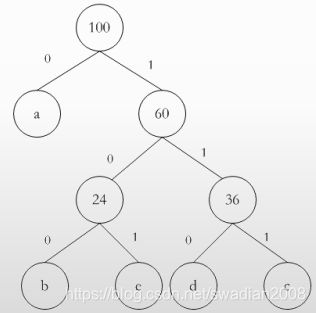
根据题意构造哈夫曼树如下。

• 第一步，从a,b,c,d,e中选取两个频率最小的构造成一棵小的树，题中频率最小的是b和e，构造父亲节点(H)就是（b+e=24）；
• 第二部，除去b和e后，从a,c,d和构造父亲节点(H)中再选取两个最小的构成一个小的树，根据题意选取d和c，构造父亲节点(F)就是（d+c=36）；
• 第三步，除去c,d后，从a和构造父亲节点(H)，构造父亲节点(F)中，选取两个最小的，根据题意，选择构造父亲节点(H)和构造父亲节点(F)，得新的构造父亲节点(G)为（24+36=60）
• 第四步，选取剩下的a和构造父亲节点(G)，组成一棵新的树，新树的根节点为（60+40=100）

a的编码：0，b的编码100，c的编码111，d的编码110,e的编码：101。

单词“cade”的编码就是“1110110101”。

压缩前，属于定长编码，每个字符用3位编码（2^3 > 5），无压缩的编码长度是：3*(40%+10%+20%+16%+14%)=3*100%=3

压缩后编码长度是：1*40%+3*10%+3*20%+3*16%+3*14%=2.2，压缩率：（3- 2.2）/3=27%

参考答案：A、C

8、图

图G由两个集合V和E组成，记为G=（V,E），其中V是顶点的有穷非空集合，E是V中顶点偶对（称为边）的有穷集合。

通常，也将图G 的顶点集和边集分别记为V(G)和E(G)。E(G)可以是空集。若 E(G)为空，则图G只有顶点而没有边。

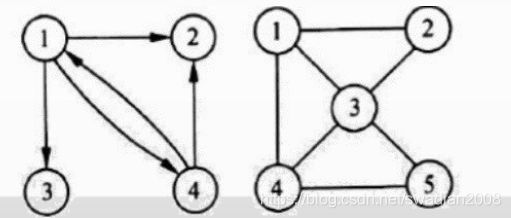
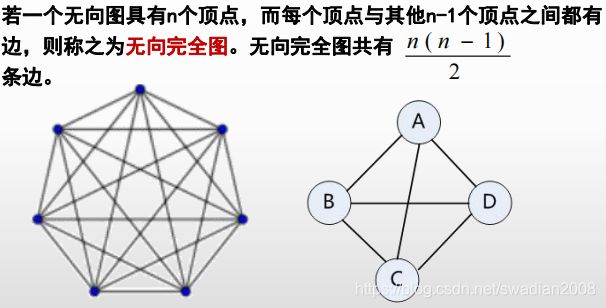
（1）无向完全图和有向完全图

1.1-无向完全图——每个顶点与其他顶点之间都有边

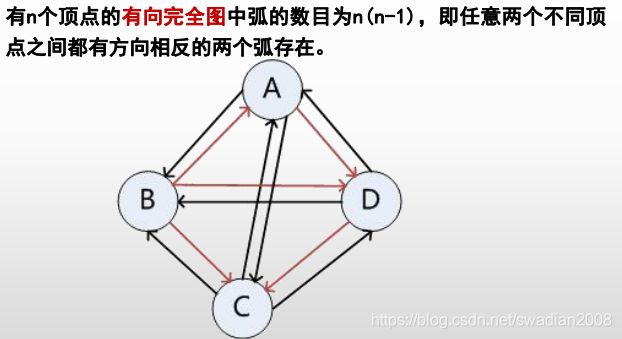
1.2-有向完全图——任意两个不同顶点之间都有方向相反的两个弧存在

（2）连通图和强连通图

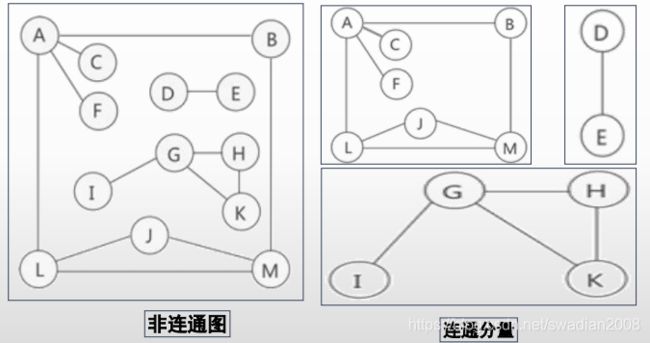
2.1-连通图

无向图中，任意两个顶点都是连通的

在无向图G中，若从顶点vi<到顶点vj有路径，则称顶点vi和顶点vj 是连通的。如果无向图G中任意两个顶点都是连通的，则称其为连通图。无向图的极大连通子图称为G的连通分量。

2.2-强连通图

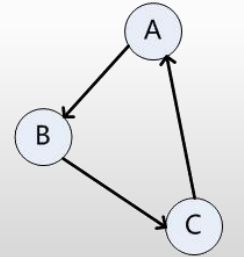
有向图中，任意两个顶点都是联通的

有向图中，若任意两个顶点 Vi 和 Vj，满足从 Vi 到 Vj 以及从 Vj 到 Vi 都连通，也就是都含有至少一条通路，则称图为强连通图。有向图中的极大连通子图称为有向图的强连通分量。

（3）图的存储——邻接矩阵和邻接表

3.1-邻接矩阵存储

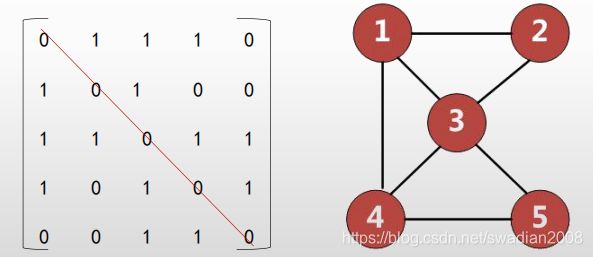
邻接矩阵可以表示每个点与点之间的关系（n*n矩阵），缺点是，如果大量的点之间没有关系，容易造成空间的浪费。

有向图的邻接矩阵不一定对称。

无向图的邻接矩阵是对称的。

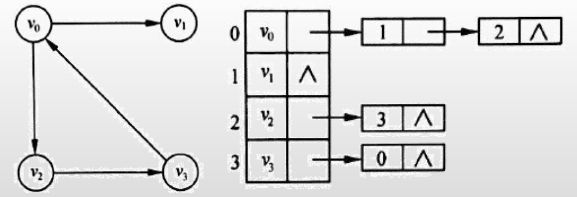
3.2-邻接表存储

在图的邻接表中，为图的每个顶点建立一个链表，且第i个链表中的结点代表与顶点i相关联的一条边或由顶点i出发的一条弧。

有n 个顶点的图，需用n个链表表示，这n个链表的头指针通常由顺序线性表存储。

（4）图的遍历

图的遍历是指从某个顶点出发，沿着某条搜索路径对图中的所有顶点进行访问且只访问一 次的过程。

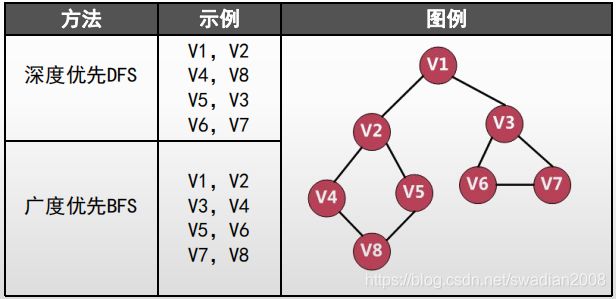
深度优先——>相当于树的前序遍历

广度优先——>相当于树的层序遍历

典型真题一

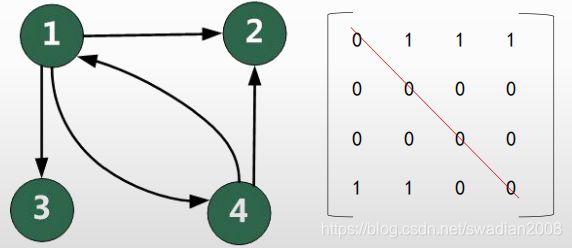
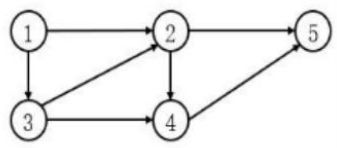
对于如下所示的有向图，其邻接矩阵是一个（）的矩阵，采用邻接链表存储时顶点的表结点个数为2，顶点5的表结点个数为0，顶点2和3的表结点个数分别为（）。

• A.5 *5         B.5*7
• C.7*5          D.7*7
• A.2.1          B. 2.2
• C.3.4          D.4.3

试题分析

5个结点的有向图若采用邻接矩阵存储是一个5*5 的矩阵， 若采用邻接表的方式存储，顶点2和3的表结点个数分别为2、2。

参考答案：A、B

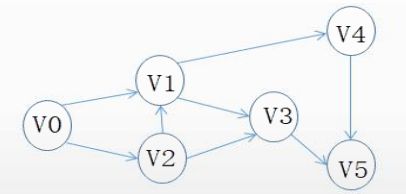
典型真题二

• A.v0、v1、v2、v3、v4、v5
• B.v0、v2、v4、 v5、v1、v3
• C.v0、v1、v3、v5、v2、v4
• D.v0、v2、v4、v3、v5、v1

试题分析

图中，V1和V2没有先后顺序，V3和V4没有先后顺序。

参考答案：B、A