图像处理:Retinex算法
目录
前言
概念介绍
Retinex算法理论
单尺度Retinex(SSR)
多尺度Retinex(MSR)
多尺度自适应增益Retinex(MSRCR)
Opencv实现Retinex算法
SSR算法
MCR算法
MSRCR算法
效果展示
总结
参考文章
前言
这里将会介绍一种图像增强的算法——Retinex算法。在查找资料的过程中,我发现对于这一部分的讲解并不是很清楚,所以这里我觉得有必要写一篇通俗且清晰的介绍。这里主要介绍三种Retinex算法的变种,它们在原有的Retinex算法的基础上做了进一步的改进和优化。
概念介绍
Retinex是一种常用于图像增强的算法,其核心思想是在保留图像细节信息的前提下,调整图像的对比度和亮度。Retinex算法主要有三种不同的实现方式:单尺度Retinex(SSR)、多尺度Retinex(MSR)和多尺度自适应增益Retinex(MSRCR)。
- 单尺度Retinex算法假设图像中的光照变化主要集中在低频分量上,因此只需对图像进行一次滤波处理即可去除低频分量,然后对得到的中高频分量进行增强。
- 多尺度Retinex算法将图像分解成不同尺度的图像,对每个尺度的图像进行增强,以保留不同尺度的细节信息。
- 多尺度自适应增益Retinex算法综合了前两种算法,先分解成不同尺度的图像,然后使用自适应增益函数对每个尺度的图像进行增强,最后重建图像以达到增强效果。
Retinex算法理论
Retinex的理论基础是三色理论和颜色恒常性。
这意味着物体的颜色是由它对红、绿、蓝三种光线的反射能力来决定的,而不是由反射光强度的绝对值来决定的。同时,物体的颜色也不会受到光照不均匀性的影响,具有一致性。
Retinex模型利用这种颜色恒常性,可以在动态范围压缩、边缘增强和颜色恒常三个方面打到平衡,因此可以对各种不同类型的图像进行自适应的增强,不同于传统的只能增强图像某一类特征的方法。
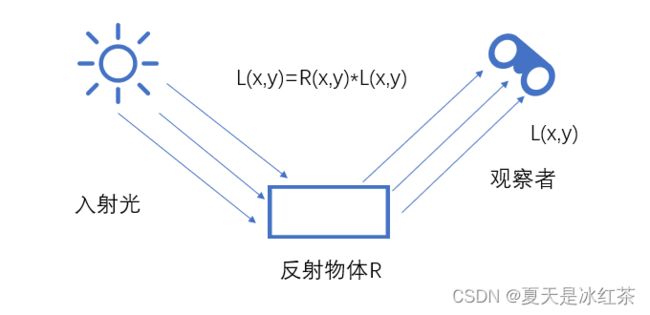
Retinex理论认为图像是由照度图像与反射图像组成。照度图像指的是物体的入射分量的信息,用表示;反射图像指的是物体的反射部分,用表示。公式:
同时,由于对数形式与人类在感受亮度的过程属性最相近,因此将上述过程转换到对数域进行处理,这样做也将复杂的乘法转换为加法:
Retinex算法的流程一般包括以下几个步骤:
高斯滤波:对输入图像进行高斯模糊处理,以消除图像中的噪声和细节。
计算照度图像:将处理后的图像转换为对数空间,并通过高斯滤波计算出照度图像,即物体的入射分量信息。
计算反射图像:通过计算原始图像和照度图像的差异得到反射图像,即物体的反射部分。
反对数变换:将照度图像和反射图像转换回线性空间。
图像拉伸:对输出图像进行亮度调整,以增强图像的对比度和细节。
当然,上面的流程是Retinex基本框架,不同的Retinex算法可能会有不同的细节处理方式。
单尺度Retinex(SSR)
单尺度视网膜算法是 Retinex 算法中最基础的一个算法。运用的就是上面的方法:
- 将输入图像转换为对数空间:
其中,为输入图像,为对数图像。
- 对对数图像进行高斯平滑:
其中,为平滑后的对数图像,为高斯滤波核。
- 计算照度图像:
其中,为照度图像,即物体的入射分量信息。
- 计算反射图像:
其中,为反射图像,即物体的反射部分。
- 将照度图像和反射图像进行指数变换:
其中,和分别为指数变换后的照度图像和反射图像。
- 对输出图像进行亮度调整:
其中,为输出图像,为反射图像中的最大值。通过将反射图像归一化到[0,1]区间,再将其放大到[0, 255]区间,可以增强图像的对比度和细节。
需要注意的是,SSR算法中只使用了一个固定的高斯滤波尺度(没有使用高斯滤波,只是高斯核),因此称为单尺度Retinex。虽然算法简单,但在一些场景下仍能取得较好的效果。
多尺度Retinex(MSR)
1.将原始图像分解为多个尺度的图像
......
其中为高斯滤波器,表示第层尺度的高斯核尺度,表示第层尺度的图像。
2.对每一层尺度图像进行 Retinex 处理
其中表示第层尺度的反射分量,表示第层尺度的光照分量,表示第层尺度的增强后的图像。
3.将各层增强后的图像进行加权融合,得到最终的增强图像
其中表示第层尺度的权重。
综上所述,多尺度Retinex算法与单尺度Retinex算法的不同之处在于对图像的分解方式,它将原始图像分解为多个尺度的图像,然后对每一层尺度的图像进行Retinex处理,最后进行加权融合得到最终的增强图像。
多尺度自适应增益Retinex(MSRCR)
MSRCR算法是在MSR算法的基础上进一步改进而来的,主要是通过自适应增益控制算法的方式来实现对图像的增强。相对于MSR算法,MSRCR算法主要增加了以下步骤:
- 多尺度分解:将原始图像分解成不同尺度的子图像。
- 对数域操作:对每个尺度下的子图像进行对数变换,得到对数域图像。
- 自适应增益控制:对于每个尺度下的对数域图像,通过计算每个像素点周围像素点的标准差,来确定该像素点的增益系数,即:
其中,表示像素点的增益系数,表示像素点周围的像素点的标准差,为一个常数,用于控制增益系数的大小。
- 增强处理:对每个尺度下的对数域图像进行乘法增强,即:
其中,为增强后的像素值,为原始对数域图像的像素值。
- 逆对数变换:对每个尺度下的增强后的对数域图像进行逆对数变换,得到增强后的子图像。
- 尺度合成:将所有增强后的子图像进行合成,得到最终增强后的图像。
需要注意的是,MSRCR算法中的增益系数计算公式与MSR算法不同,增加了常数,这样可以控制增益系数的大小,避免增益系数过大导致图像的过度增强。此外,MSRCR算法中还增加了多尺度分解、增强处理和尺度合成等步骤,进一步提高了对不同尺度、不同光照条件下图像的增强效果。
Opencv实现Retinex算法
在python中是没有集成的第三方库的函数(可能调查不到位),这里我们就根据它的这个原理来实现这三种Retinex算法。
在我这里我讲详细一点,尽量让大家去理解,而不是只是套代码去用。
SSR算法
def SSR(img, sigma):
img_log = np.log1p(np.array(img, dtype="float") / 255)
img_fft = np.fft.fft2(img_log)
G_recs = sigma // 2 + 1
result = np.zeros_like(img_fft)
rows, cols, deep = img_fft.shape
for z in range(deep):
for i in range(rows):
for j in range(cols):
for k in range(1, G_recs):
G = np.exp(-((np.log(k) - np.log(sigma)) ** 2) / (2 * np.log(2) ** 2))
result[i, j] += G * img_fft[i, j]
img_ssr = np.real(np.fft.ifft2(result))
img_ssr = np.exp(img_ssr) - 1
img_ssr = np.uint8(cv2.normalize(img_ssr, None, 0, 255, cv2.NORM_MINMAX))
return img_ssr实现思路:
将输入图像转换为了对数空间。/255将像素值归一化到0到1之间,np.log1p取对数并加1是为了避免出现对数运算中分母为0的情况。二维离散傅里叶变换将图像从空间域变换到频率域,可以提取出图像中的频率信息。G_recs是用于计算高斯核的半径,result用于最后三通道的叠加。然后循环用于计算加权后的频率域图像,再逆二维离散傅里叶变换,得到反射图像,对反射图像进行指数变换,得到最终的输出图像。
MCR算法
def MSR(img, scales):
img_log = np.log1p(np.array(img, dtype="float") / 255)
result = np.zeros_like(img_log)
img_light = np.zeros_like(img_log)
r, c, deep = img_log.shape
for z in range(deep):
for scale in scales:
kernel_size = scale * 4 + 1
# 高斯滤波器的大小,经验公式kernel_size = scale * 4 + 1
sigma = scale
img_smooth = cv2.GaussianBlur(img_log[:, :, z], (kernel_size, kernel_size), sigma)
img_detail = img_log[:, :, z] - img_smooth
result[:, :, z] += cv2.resize(img_detail, (c, r))
img_light[:, :, z] += cv2.resize(img_smooth, (c, r))
img_msr = np.exp(result+img_light) - 1
img_msr = np.uint8(cv2.normalize(img_msr, None, 0, 255, cv2.NORM_MINMAX))
return img_msr实现思路:
MSR算法在图像增强中与SSR不同的是,它不需要进行频域变换,它主要是基于图像在多个尺度下的平滑处理和差分处理来提取图像的局部对比度信息和全局对比度信息,从而实现对图像的增强。
在 MSR 算法中,先对图像进行对数变换得到对数图像,然后在不同的尺度下,使用高斯滤波对图像进行平滑处理,得到不同尺度下的平滑图像。接着,通过将对数图像和不同尺度下的平滑图像进行差分,得到多个尺度下的细节图像。最后,将这些细节图像加权融合,输出最终的增强图像。
关于尺度选择
经验上来说,选择的尺度范围通常是1到10左右,也就是说选择3到4个不同的尺度值进行多尺度处理。尺度的大小可以取任意奇数或偶数,但是建议就选奇数尺度大小,这样可以保证在进行高斯滤波时,中心像素周围的权值更大,从而更好地保留图像的细节信息。
MSRCR算法
def MSRCR(img, scales, k):
img_log = np.log1p(np.array(img, dtype="float") / 255)
result = np.zeros_like(img_log)
img_light = np.zeros_like(img_log)
r, c, deep = img_log.shape
for z in range(deep):
for scale in scales:
kernel_size = scale * 4 + 1
# 高斯滤波器的大小,经验公式kernel_size = scale * 4 + 1
sigma = scale
G_ratio=sigma**2/(sigma**2+k)
img_smooth = cv2.GaussianBlur(img_log[:, :, z], (kernel_size, kernel_size), sigma)
img_detail = img_log[:, :, z] - img_smooth
result[:, :, z] += cv2.resize(img_detail, (c, r))
result[:, :, z]=result[:, :, z]*G_ratio
img_light[:, :, z] += cv2.resize(img_smooth, (c, r))
img_msrcr = np.exp(result+img_light) - 1
img_msrcr = np.uint8(cv2.normalize(img_msrcr, None, 0, 255, cv2.NORM_MINMAX))
return img_msrcr实现思路:
这一部分我只是将MSR的实现进行了扩充,添加了自适应增益控制,即是对于每个尺度下的对数域图像,通过计算每个像素点周围像素点的标准差,来确定该像素点的增益系数。这里的k值为一个常数,我的建议是取10-20之间,当k取值较小时,图像的细节增强效果比较明显,但会出现较强的噪点,当k取值较大时,图像的细节增强效果不明显,但噪点会减少。因此,需要根据实际应用场景进行适当的调整。
效果展示
 上(左)原图,上(右)SSR,下(左)MSR,下(右)MSRCR
上(左)原图,上(右)SSR,下(左)MSR,下(右)MSRCR
if __name__=="__main__":
path=r'./Images/AI2.png'
img=cv2.imread(path)
imgSSR=SSR(img,7)
imgMSR=MSR(img, [1, 3, 5])
imgMSRCR=MSRCR(img,[1,3,5],12)
imgStack=zjr.stackImages(0.6,([img,imgSSR],[imgMSR,imgMSRCR]))
cv2.imshow("retinex",imgStack)
cv2.waitKey(0)
总结
在尝试实现像Retinex这种没有集成函数的算法时,我遇到了一些困难。这些算法需要深入理解其原理和流程,并在代码具体实现。为了解决这些问题,我参考了其他大佬的代码,但大多数代码并不完整,经常出现报错。我也只能依照自己对算法的理解来实现其功能,可能存在部分错误。因此,我希望可以与大家共同讨论,一起学习和进步。
参考文章
(6条消息) Retinex 算法_chaiky的博客-CSDN博客
(7条消息) Retinex算法详解_ChenLee_1的博客-CSDN博客
(6条消息) Retinex图像增强算法——SSR,MSR,MSRCR,MSRCP,autoMSRCR_Chaoy6565的博客-CSDN博客
传统图像处理——图像增强Retinex - 知乎 (zhihu.com)
Retinex图像增强算法理论基础 - 知乎