几何向量:向量到平面投影和LookAt
在研究所保密开发完后回来隔离两波,已经接近四五个月没碰外网电脑了,可以说是活成了原始人。
因为某些开发细节原因,需要实现向量投影和LookAt功能,记录一下。
首先实现向量到平面投影,如下:
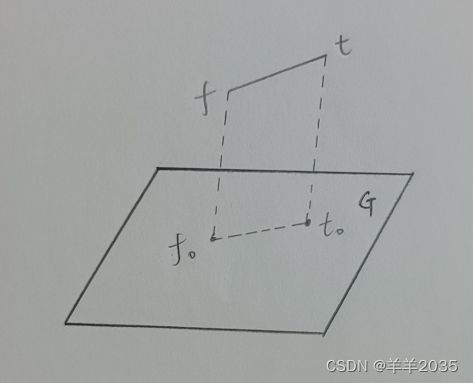
前面我们聊过点向量平面之间的关系,好像写过好几篇文章,这里就从简。其实计算投影无非就是计算P在平面G上的投影P0,计算如下:
 我们根据平面G方程得到ABCD分量,然后求出系数k,带入X0、Y0、Z0代数式就能达到P0坐标了,如下:
我们根据平面G方程得到ABCD分量,然后求出系数k,带入X0、Y0、Z0代数式就能达到P0坐标了,如下:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class PALAVectorProjection : MonoBehaviour
{
public Transform ground0;
public Transform ground1;
public Transform ground2;
public Transform from;
public Transform to;
void Start()
{
}
void Update()
{
Vector3 g0 = ground0.position;
Vector3 g1 = ground1.position;
Vector3 g2 = ground2.position;
Debug.DrawLine(g0, g1, Color.black);
Debug.DrawLine(g1, g2, Color.black);
Debug.DrawLine(g2, g0, Color.black);
Vector3 f = from.position;
Vector3 t = to.position;
Debug.DrawLine(f, t, Color.yellow);
Vector3 f0 = GetProjectPoint(f, g0, g1, g2);
Vector3 t0 = GetProjectPoint(t, g0, g1, g2);
Debug.DrawLine(f0, t0, Color.white);
}
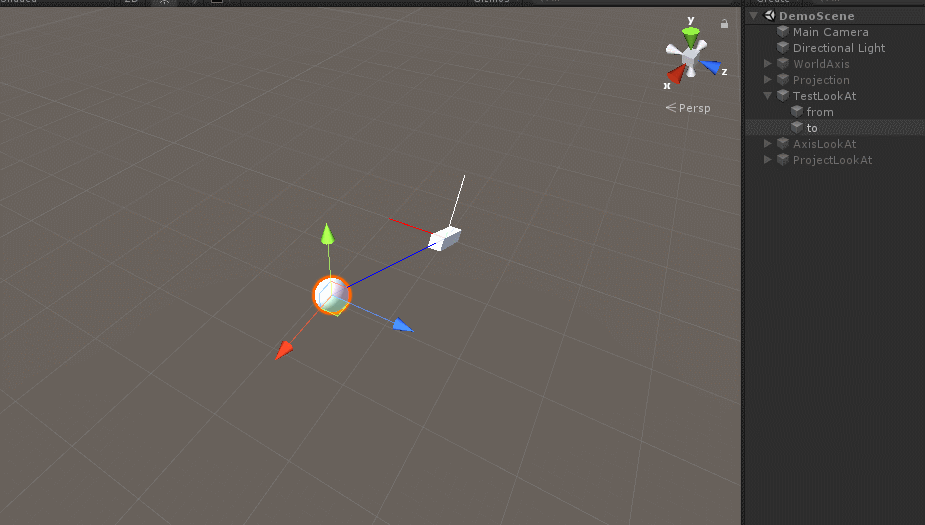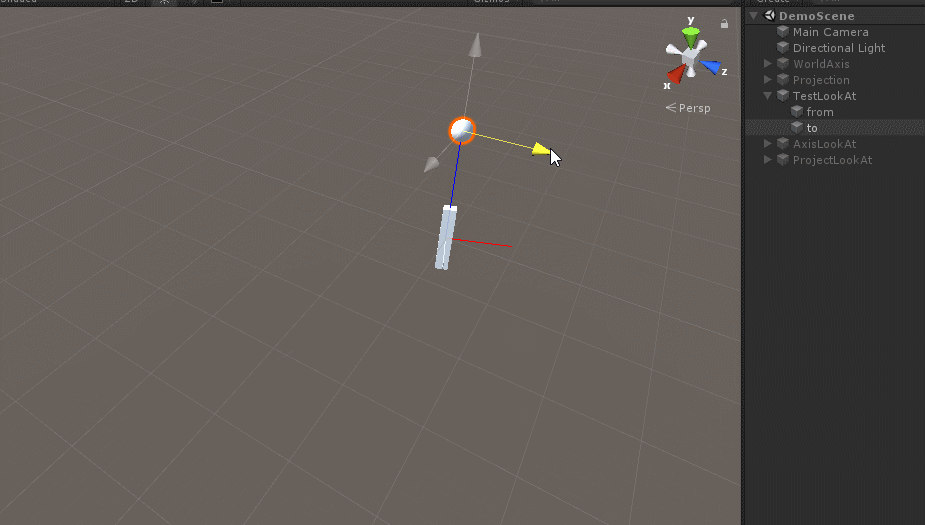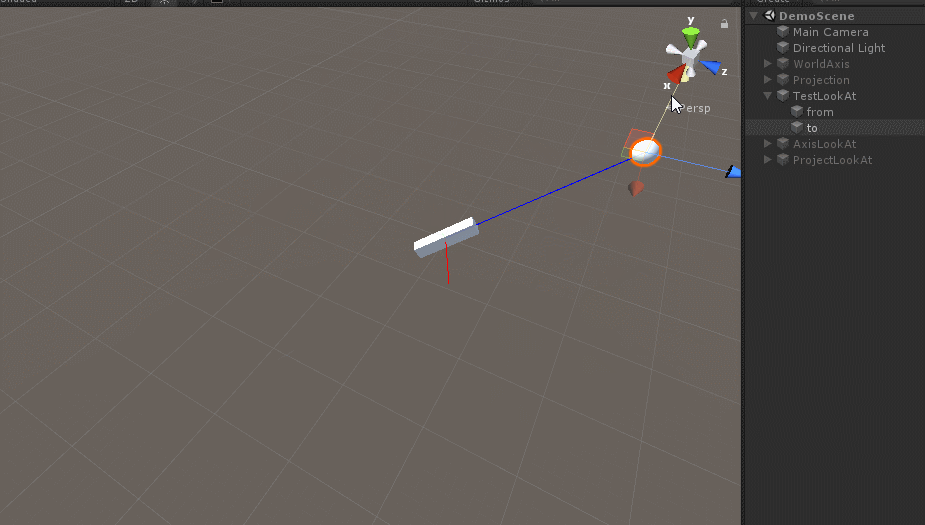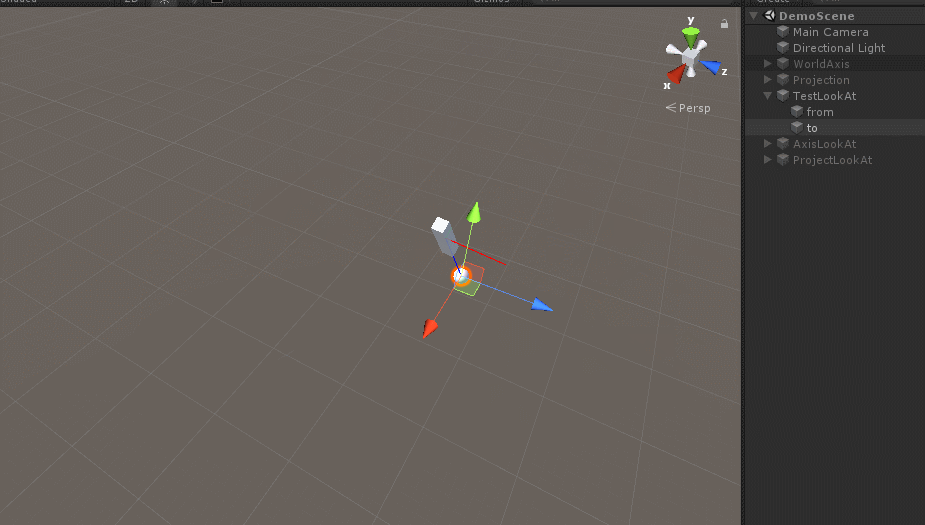
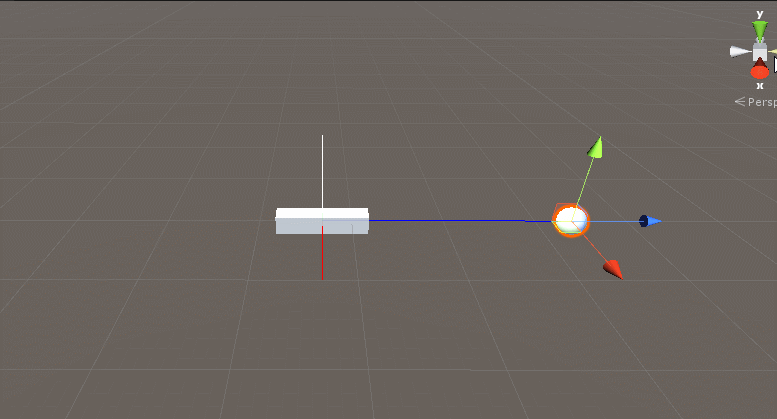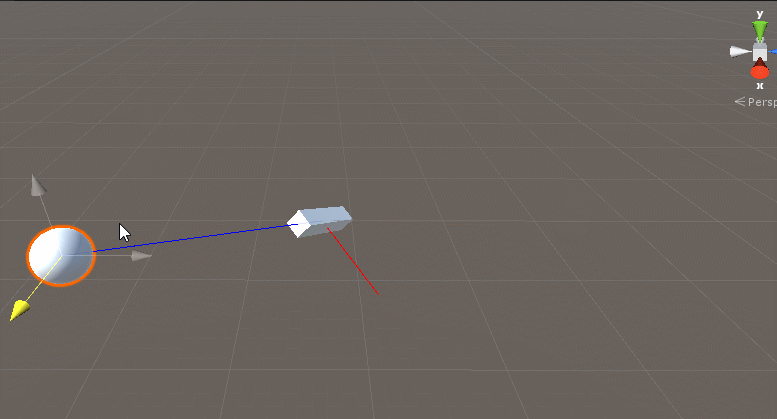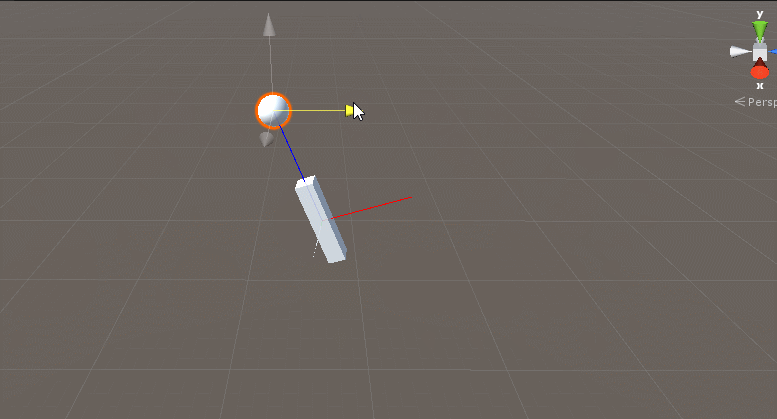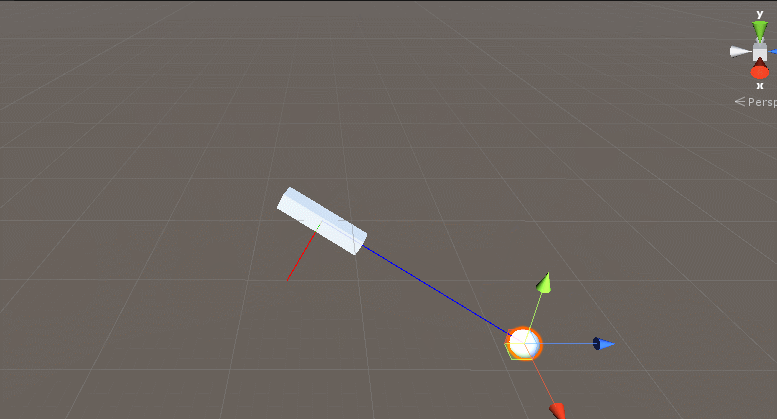
/// 效果如下:
白色的线段是黄色线段在平面G上的投影。
继续,接下来要实现一下LookAt功能,首先看一下unity的API,如下:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class PALATestLookAt : MonoBehaviour
{
public Transform from;
public Transform to;
void Start()
{
}
void Update()
{
Debug.DrawLine(from.position, to.position, Color.blue);
Debug.DrawLine(from.position, from.position + from.right, Color.red);
Debug.DrawLine(from.position, from.position + from.up, Color.green);
from.LookAt(to);
}
}
朝向计算就是半角向量的180度旋转计算,设Z轴上模长等于ft模长的向量ft0绕半角向量ft1旋转180度,就变成了向量ft
实现一下:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class PALAAxisLookAt : MonoBehaviour
{
public Transform from;
public Transform to;
void Start()
{
}
void Update()
{
Debug.DrawLine(from.position, to.position, Color.blue);
Debug.DrawLine(from.position, from.position + from.right, Color.red);
Debug.DrawLine(from.position, from.position + from.up, Color.green);
GetAxisLookAt();
}
/// 效果如下:

这是一种LookAt的实现方法。
继续探索,现实中存在的朝向计算,坦克就是很好的例子,如下:

坦克的炮台可以想象为绕世界坐标Y轴旋转,炮筒想象成绕本地坐标X轴旋转,稍微绘制一下,如下:
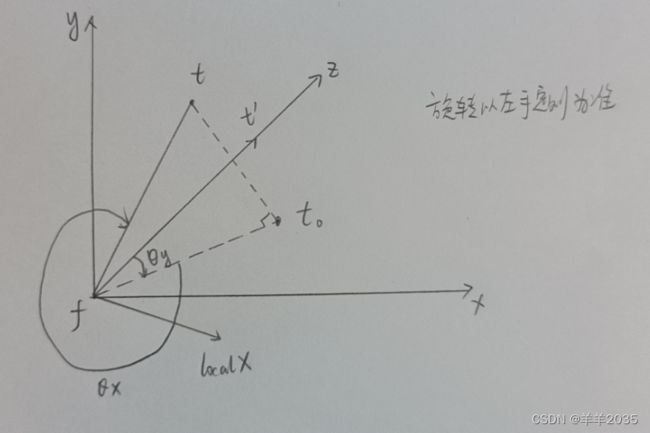
首先求得ft在平面xfz上的投影ft0,ft’(fz)与投影ft0绕世界坐标Y轴夹角θy度就是“炮台”的旋转度数,然后ft0与ft绕本地坐标X轴夹角θx度就是“炮筒”的旋转度数,旋转以左手定则为准,那么接下来代码实现:
using System.Collections;
using System.Collections.Generic;
using System.Reflection;
using UnityEngine;
public class PALAProjectionLookAt : MonoBehaviour
{
public Transform from;
public Transform to;
void Start()
{
Application.targetFrameRate = 60;
}
void Update()
{
Vector3 f = from.position;
Vector3 t = to.position;
Vector3 lx = f + from.right;
Vector3 ly = f + from.up;
Vector3 lz = f + from.forward;
Debug.DrawLine(f, lx, Color.red);
Debug.DrawLine(f, ly, Color.green);
Debug.DrawLine(f, t, Color.black);
GetProjectLookAt();
}
/// 效果如下:
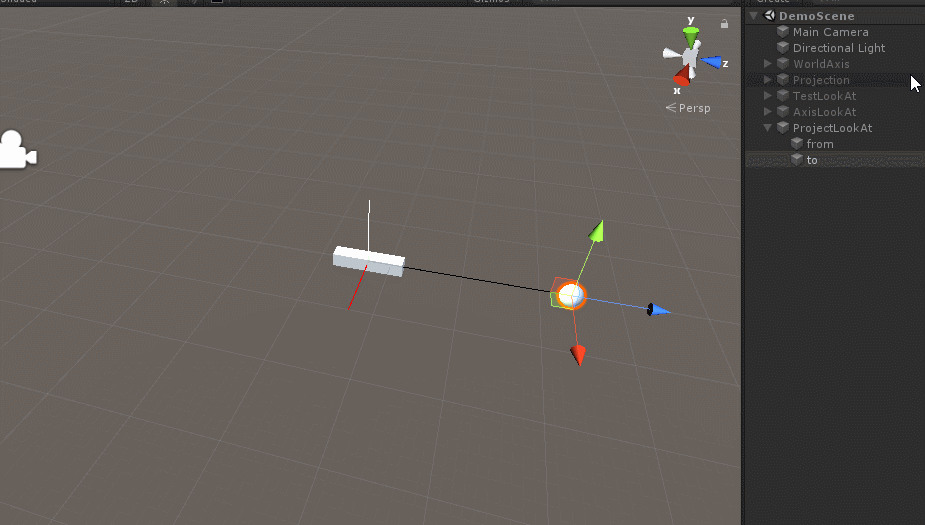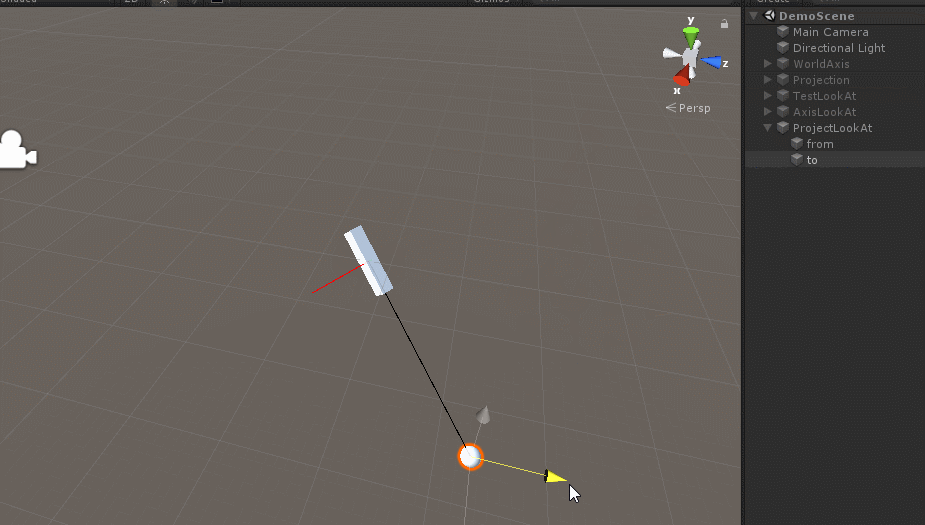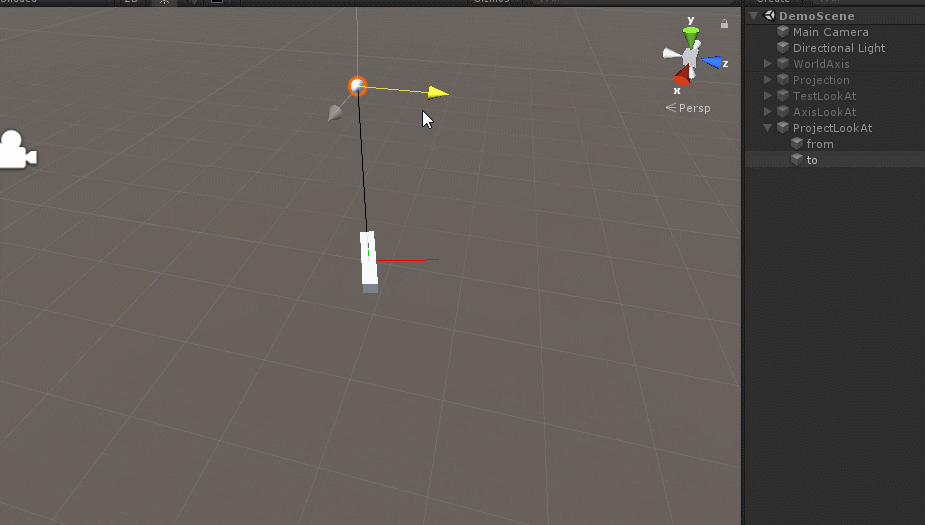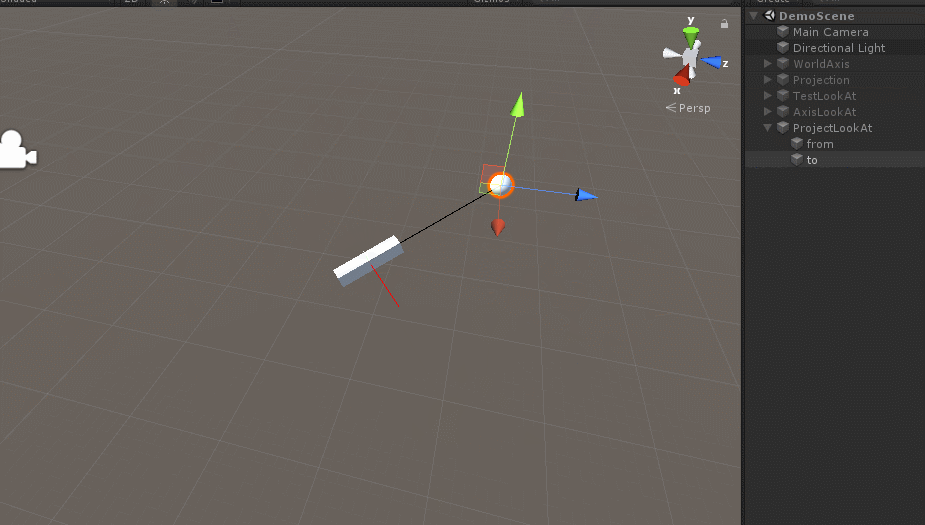
这也是一种LookAt的实现方法。
还有一种LookAt实现方法,通过叉乘向量旋转,如下:

可以看出,计算得到fc叉积向量,再计算得到fdir到ft的旋转角度θ,就能计算出LookAt朝向,代码如下:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class PALACrossLookAt : MonoBehaviour
{
public Transform from;
public Transform to;
void Start()
{
}
void Update()
{
Debug.DrawLine(from.position, to.position, Color.blue);
Debug.DrawLine(from.position, from.position + from.right, Color.red);
Debug.DrawLine(from.position, from.position + from.up, Color.green);
GetCrossLookAt();
}
/// 这也是一种LookAt的实现方式。
自己实现LookAt的好处是可以自由控制朝向轴,可能API不一定适合开发需求。
好,以后有时间继续。