k-means聚类算法（matlab实现）

k-means聚类算法

---

前言

k-means聚类算法是硬聚类算法的一种，即在n纬欧几里得空间把n个样本数据分为k类。首先根据用户要确定聚类的数目k,随机性的选取k个样本，把每一个对象成为一个种子，每一个种子代表一个类的中心，对其余的每个对象，采用近邻原则，将它们赋给最近的类。重新计算在每个类中对象的均值新形成的聚类中心，重复进行这个过程直到函数式收敛为止。

k-means聚类算法的改进：
k-means++算法链接: https://blog.csdn.net/qq_40276082/article/details/130237784?spm=1001.2014.3001.5501

---

一、k-means聚类算法简介

K-means算法是一种无监督学习算法，用于将n个数据点划分为k个簇（cluster）。该算法的主要思想是将数据点划分为k个簇，使得同一簇内的数据点彼此相似，而簇间的数据点相差较大。
K-means算法是一种迭代算法，其核心是利用距离度量来度量不同数据点之间的相似度，并利用质心来表示簇的中心。在每次迭代中，算法通过更新簇质心和重新分配数据点来优化簇的划分。具体来说，算法的步骤如下：

初始化：随机选择k个数据点作为初始质心，将所有数据点分配到距离最近的质心所在的簇中。

簇分配：对于每个数据点，计算其到k个质心的距离，将其分配到距离最近的质心所在的簇中。

更新质心：对于每个簇，计算其所有数据点的平均值，将其作为新的质心。

重复步骤2和步骤3，直到簇的分配不再改变或达到最大迭代次数。

二、k-means聚类算法步骤

三、代码实现

代码如下（示例）：

clc
clear
a=[22.5661	113.9808	66
22.6862	113.9405	65.5
22.5648	114.2446	75
22.5589	113.9507	65.5
22.559	114.2413	75
22.5628	113.9566	65.5
22.5	113.8957	66
22.5249	113.9309	65.5
22.5191	113.9358	65.5
22.4982	113.8985	66
23.0057	112.9708	75
23.0391	113.0726	66
22.9408	113.0627	72.5
23.0408	113.1116	65
23.0387	113.1074	65.5
23.0042	113.0704	66.5
23.0489	113.0719	66
23.0104	113.1463	66
23.0058	113.1356	65.5
22.8821	113.2179	68.5
23.0401	113.1075	65.5
22.9946	113.1409	72
22.9789	113.0167	72
22.9456	113.09	72
23.0441	113.1258	65.5
];
N=length(a(:,1));
X=[];
Y=[];

for j=1:N
    f=a(j,1);
w=a(j,2);
X=vertcat(X,f);
Y=vertcat(Y,w);

end
N=length(X(:,1));
plot(X, Y, 'k*'); % 绘出原始的数据点
xlabel('X');
ylabel('Y');
title('聚类之前的数据点');
n = 2; %将所有的数据点分为两类
m = 1; %迭代次数
eps = 1e-7; % 迭代结束的阈值
u1 = [X(1),Y(1)]; %初始化第一个聚类中心
u2 = [X(2),Y(2)]; %初始化第二个聚类中心
U1 = zeros(2,100);
U2 = zeros(2,100); %U1,U2 用于存放各次迭代两个聚类中心的横纵坐标
U1(:,2) = u1;
U2(:,2) = u2;
D = zeros(2,N); %初始化数据点与聚类中心的距离
while(abs(U1(1,m) - U1(1,m+1)) > eps || abs(U1(2,m) - U1(2,m+1) > eps || abs(U2(1,m) - U2(1,m+1)) > eps || abs(U2(2,m) - U2(2,m+1)) > eps))
    m = m +1;
    % 计算所有点到两个聚类中心的距离
for i = 1 : N
    D(1,i) = sqrt((X(i) - U1(1,m))^2 + (Y(i) - U1(2,m))^2);
end
for i = 1 : N
    D(2,i) = sqrt((X(i) - U2(1,m))^2 + (Y(i) - U2(2,m))^2);
end
A = zeros(2,N); % A用于存放第一类的数据点
B = zeros(2,N); % B用于存放第二类的数据点
for k = 1: N
    [MIN,index] = min(D(:,k)); 
    if index == 1  % 点属于第一个聚类中心
        A(1,k) = X(k);
        A(2,k) = Y(k);
    else           % 点属于第二个聚类中心
        B(1,k) = X(k);
        B(2,k) = Y(k);
    end
end
indexA = find(A(1,:) ~= 0); % 找出第一类中的点
indexB = find(B(1,:) ~= 0); % 找出第二类中的点
U1(1,m+1) = mean(A(1,indexA));
U1(2,m+1) = mean(A(2,indexA));
U2(1,m+1) = mean(B(1,indexB));
U2(2,m+1) = mean(B(2,indexB)); % 更新两个聚类中心
end
figure;
plot(A(1,indexA) , A(2,indexA), '*b'); % 作出第一类点的图形
hold on
plot(B(1,indexB) , B(2,indexB), '*g'); %作出第二类点的图形
hold on
centerx = [U1(1,m) U2(1,m)]
centery = [U1(2,m) U2(2,m)]
plot(centerx , centery, 'or'); % 画出两个聚类中心点
xlabel('X');
ylabel('Y');
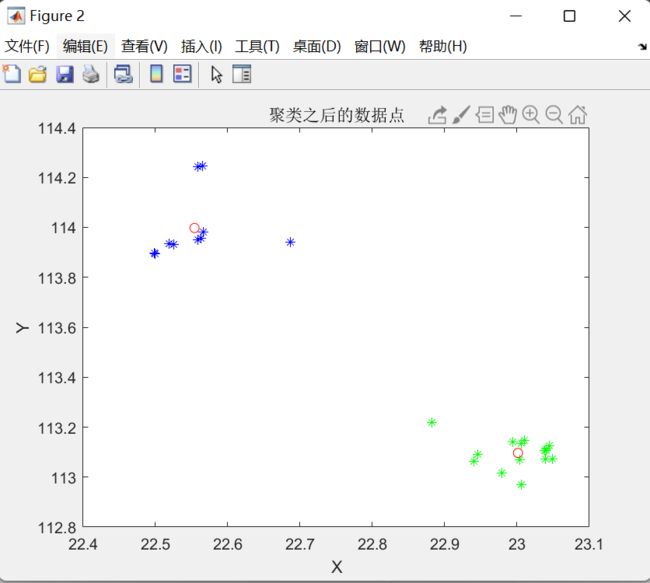
title('聚类之后的数据点');
disp(['迭代的次数为:',num2str(m)]);

运行结果：

---

总结

K-means算法的优点在于简单、易于实现，适用于大型数据集。但是，它也有一些缺点。首先，K-means算法对于数据点分布的先验知识敏感，且容易收敛到局部最优解。其次，K-means算法要求每个簇的大小相等，这在某些情况下可能会导致不合理的结果。最后，K-means算法对于噪声和异常值敏感，因为它只考虑数据点之间的欧几里德距离，而没有考虑其他距离度量或数据结构。