数据结构 总结9 内部排序

基础知识

排序方法的稳定与不稳定

• 稳定的排序方法：在排序前后，含相等关键字的记录的相对位置保持不变
• 不稳定的的排序方法：含相等关键字的记录的相对位置有可能改变

内部排序与外部排序

• 内部排序：在排序过程中，只使用计算机的内存存放待排序记录
• -外部排序：排序期间文件的全部记录不能同时存放在计算机的内存中，要借助计算机的外存才能完成排序
• 内外存之间的数据交换次数是影响外部排序速度的主要因素

练习题

1. 外部排序是把外存文件调入内存,可利用内部排序的方法进行排序,因此排序所花的时间取决于内部排序的时间（❌）
2. 顺序序列(101,88,46,70,34,39,45,58,66,10）是堆 （✔）
3. 当待排序记录已经从小到大排序或者已经从大到小排序时，快速排序的执行时间最省（❌）
4. 在执行某个排序算法过程中，出现了排序码朝着最终排序序列位置相反方向移动，则该算法是不稳定的（❌）
5. 设表中元素的初始状态是按关键值递增的，分别用堆排序，快速排序，冒泡排序和归并排序方法对其进行排序（按递增顺序）， 冒泡排序最省时间，快速排序最费时间（✔）
6. 数据序列（2，1，4，9，8，10，6，20）只能是下列排序算法中的( )的两趟排序后的结果
   A. 插入排序
   B. 冒泡排序
   C. 选择排序
   D. 快速排序
7. 排序趟数与序列的原始状态有关的排序方法是
   A. 插入
   B. 选择
   C. 冒泡
   D. 快速
8. 若不考虑基数排序，则在排序过程中，主要进行的两种基本操作是关键字的比较和记录的移动（✔）
9. 在任何情况下，归并排序都比直接插入排序快（❌）
10. 下列排序算法中,（ ）算法可能会出现下面情况：在最后一趟开始之前，所有元素都不在其最终的位置上。
    A. 堆排序
    B. 冒泡排序
    C. 快速排序
    D. 插入排序
11. 对初始状态为递增序列的表按递增顺序排序，最浪费时间的是（ ）算法，最省时间的是（ ）算法
    A. 堆排序
    B. 快速排序（最费）
    C. 插入排序（最省）
    D. 归并排序
    解析：快排退化为冒泡排序
12. 下列排序算法中 ( ) 排序在一趟结束后不一定能选出一个元素放在其最终位置上。
    A. 选择排序
    B. 冒泡排序
    C. 归并排序
    D. 堆排序
    解析：比如插入排序进行升序排序时候，最后一个是最小值的情况
13. 数据序列（8，9，10，4，5，6，20，1，2）只能是下列排序算法中的( )的两趟排序后的结果
    A. 选择排序
    B. 冒泡排序
    C. 插入排序
    D. 堆排序
    解析：前三个元素是有序的
14. 若要求尽可能快地对序列进行稳定的排序，则应选（ )
    A. 快速排序
    B. 归并排序
    C. 冒泡排序
    解析：快速排序快，但不稳定，冒泡慢于归并
15. 数据序列（2，1，4，9，8，10，6，20）只能是下列排序算法中的( )的两趟排序后的结果
    A. 插入排序
    B. 冒泡排序
    C. 选择排序
    D. 快速排序
    解析：第一次枢纽为4，第二次枢纽为20
16. 下列排序算法中，占用辅助空间最多的是( )
    A. 归并排序
    B. 快速排序
    C. 希尔排序
    D. 堆排序
17. 下面给出的四种排序法中( )排序法是不稳定性排序法。
    A. 插入
    B. 冒泡
    C. 二路归并
    D. 堆排序
18. 若R中有10000个元素，如果仅要求求出其中最大的10个元素，则最省时间的方法是（ ）
    A. 堆排序
    B. 希尔排序
    C. 快速排序
    D. 基数排序
    解析：堆排序可以直接得出指定范围的局部有序结果，其它的排序方法都需要全部排完后才能获取局部结果
19. 将两个长度分别为n，m的递增有序顺序表归并成一个有序顺序表，其元素最多的比较次数是（ ）
    A. n
    B. m+n
    C. MIN(m,n)
    D. m+n-1
20. 若一组记录的关键字序列为(46,79,56,38,40,84)，则利用快速排序的方法，以第1个关键字为轴得到的一次划分结果为（ ）
    A. 38,40,46,56,79,84
    B. 40,38,46,79,56,84
    C. 40,38,46,56,79,84
    D. 40,38,46,84,56,79

9.1 插入排序

直接插入排序

直接插入排序的思想：

1. 第一个记录有序（array[1]）
2. 从第二个记录（array[2]）开始，按关键字的大小将每个记录插入到已排好序的序列中
3. 一直进行到第n个记录

void InsertSort() {
    int i, j;
    for (i = 2; i <= len; ++i) {
        if (arr[i] < arr[i - 1]) {
            arr[0] = arr[i];  //复制为监视哨
            arr[i] = arr[i - 1];  //
            for (j = i - 2; arr[0] < arr[j]; --j)
                arr[j + 1] = arr[j];  //记录后移
            arr[j + 1] = arr[0];
        }
    }
}
排序过程  监视哨  1  2  3  4  5  6  7  8  9  10
第0次排序:   0   49 28 65 76 13 27 36 58 11 17
第1次排序:  28   28 49 65 76 13 27 36 58 11 17  //从第2个数开始比较
第2次排序:  28   28 49 65 76 13 27 36 58 11 17
第3次排序:  28   28 49 65 76 13 27 36 58 11 17
第4次排序:  13   13 28 49 65 76 27 36 58 11 17
第5次排序:  27   13 27 28 49 65 76 36 58 11 17
第6次排序:  36   13 27 28 36 49 65 76 58 11 17
第7次排序:  58   13 27 28 36 49 58 65 76 11 17
第8次排序:  11   11 13 27 28 36 49 58 65 76 17

直接插入排序算法特点

• 原序列呈正序排列时，最省时间
• 原序列程反序序列时，最费时间

算法分析

• 最好情况（顺序有序）
  比较次数 ${\sum }_{i=2}^n(1)=n-1$
  移动次数 0
• 最坏情况（逆序有序）
  比较次数 ${\sum }_{i=2}^n(i)=(n+2)(n-1)/2$
  移动次数 ${\sum }_{i=2}^n(i+1)=(n+4)(n-1)/2$
• 直接插入排序是 稳定 的排序算法
• 时间复杂度：平均 O(n²)
• 空间复杂度：O(1)

折半插入排序

折半插入排序的思想：

1. 在直接插入排序进行第i个元素时，r[1], r[2], …, r[i-1] 是一个按关键字有序的列;
2. 可以利用折半查找实现在“r[1], r[2], …, L.r[i-1]”中查找r[i]的插入位置

算法分析

• 折半插入排序是 稳定 的排序算法
• 时间复杂度：平均 O(n²)
• 空间复杂度：O(1)

9.2 希尔排序

排序思想：
将记录序列分成若干子序列，分别对每个子序列进行插入排序
例如将 n 个记录分成 d 个子序列：
{R[1], R[1+d], R[1+2d], …, R[1+kd]}
{R[2], R[2+d], R[2+2d], …, R[2+kd]}
……………………………………
{R[d], R[d+d], R[d+2d], …, R[d+kd]}
其中 d 为增量，在排序过程中从大到小逐渐缩小，最后一趟排序减至1

排序结果         1  2  3  4  5  6  7  8  9 10 11
第0次排序     : 16 25 12 30 47 11 23 36  9 18 31
第1次排序(d=5): 11 23 12  9 18 16 25 36 30 47 31 (11-16 23-25 12-36...) 
第2次排序(d=3):  9 18 12 11 23 16 25 31 30 47 36 (9-11-25-47 18-23-31-36...)
第3次排序(d=1):  9 11 12 16 18 23 25 30 31 36 37 (9 11 12 16...)

9.3 快速排序

冒泡排序

普通的冒泡排序：

void BubbleSort0(int arr[], int len) {
	int i = 0, tmp = 0;
	for (i = 0; i < len-1; i++) {
		int j = 0;
		for (j = 0; j < len-1-i; j++) {
			if(arr[j] > arr[j+1]) {
				tmp = arr[j];
				arr[j] = arr[j+1];
				arr[j+1] = tmp;
			}
		}
	}
}

• 优化一
  对于 a[]={1,2,3,4,5,6,7,8,10,9} 这组数据，按照上面的排序方式，第一趟排序后将10和9交换已经有序，接下来的8趟排序就是多余的，什么也没做。所以在交换的地方加一个标记，如果那一趟排序没有交换元素，说明这组数据已经有序，不用再继续下去。

void BubbleSort1(int arr[], int len) {
	int i = 0, tmp = 0;
	for (i = 0; i < len-1; i++) {
		int j = 0;
		int flag = 0;		 
		for (j = 0; j < len-1-i; j++) {
			if(arr[j] > arr[j+1]) {
				tmp = arr[j];
				arr[j] = arr[j+1];
				arr[j+1] = tmp;
				flag = 1;  // 标记 
			} 
		}		
		if(flag == 0) return;  // 没交换,已有序
	}
}

• 优化二
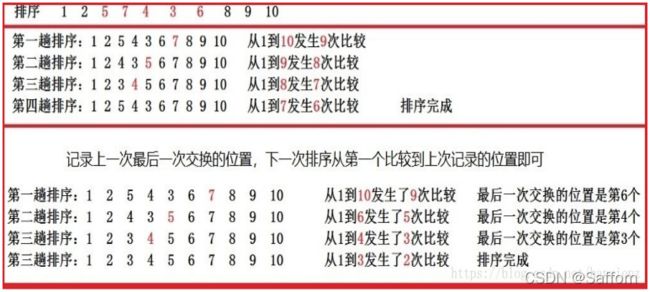
  优化一仅仅适用于连片有序而整体无序的数据 (例如：1, 2, 3, 4, 7, 6, 5) 但是对于前面大部分是无序而后边小半部分有序的数据 (1, 2, 5, 7, 4, 3, 6, 8, 9, 10) 排序效率不高对于这种类型数据，我们可以记下最后一次交换的位置，后边没有交换，必然是有序的，然后下一次排序从第一个比较到上次记录的位置结束即可
  

void BubbleSort2(int arr[], int len) {
	int i = 0, tmp = 0, flag = 0;
	int pos = 0, k = len-1;	
	for (i = 0; i < len-1; i++) {
		int j = 0;
		pos = 0;
		flag = 0;
		for (j = 0; j < k; j++) {
			if(arr[j] > arr[j+1]) {
				tmp = arr[j];
				arr[j] = arr[j+1];
				arr[j+1] = tmp;
				flag = 1;  // 标记
				pos = j;  // 交换元素后，记录最后一次交换的位置 
			} 
		}
		if(flag == 0) return;  // 没交换,已有序
		k = pos;  // 下一次比较到记录位置即可 
	}
}

• 优化三
• 一次排序可以确定两个值，正向扫描找到最大值交换到最后，反向扫描找到最小值交换到最前面。
  

void BubbleSort3(int arr[], int len) {
	int i = 0, j = 0, flag = 0;
	int pos = 0, k = len-1;
	int n = 0;  // 同时找最大值的最小需要两个下标遍历 
	
	for (i = 0; i < len-1; i++) {
		pos = 0;
		flag = 0;
		for (j = 0; j < k; j++) {
			if(arr[j] > arr[j+1]) {
				int tmp = arr[j];
				arr[j] = arr[j+1];
				arr[j+1] = tmp;
				flag = 1;  // 标记
				pos = j;  // 交换元素后，记录最后一次交换的位置 
			} 
		}
		if(flag == 0) return;  // 没交换,已有序
		k = pos;  // 下一次比较到记录位置即可
		
		for(j = k; j > n; j--) {
			int tmp = arr[j];
			arr[j] = arr[j-1];
			arr[j-1] = tmp;
			flag = 1;
		}
		n++;
		if(flag == 0) return;
	}
}

快速排序

int Partition(int low, int high)
{
    d[0] = d[low];  //用表的第一个记录作为枢纽记录
    int pivotkey = d[low].number;  //枢纽记录的关键字
    while (low < high) {  //从表的两端交替向中间扫描
        while (low < high && d[high].number >= pivotkey) --high;
        d[low] = d[high];  //将比枢纽记录关键字小的 移到低端
        while (low < high && d[low].number <= pivotkey) ++low;
        d[high] = d[low];  //将比枢纽记录关键字大的 移到高端
    }
    d[low] = d[0];  //枢纽记录归位
    return low;  //返回枢纽记录的位置
}

void QuickSort(int low, int high) {
    if (low < high) {
        int pos = Partition(low, high);  //确定枢纽位置
        QuickSort(low, pos - 1);  //对左子序列排序，不包含枢纽
        QuickSort(pos + 1, high);  //对右子序列排序，不包含枢纽
    }
}
      枢纽0 | 1  2  3  4  5  6  7  8  9  10
排序前: 49  | 49 28 65 76 13 27 36 58 11 17  //以第一个记录49作为枢纽
排序后: 49  | 17 28 11 36 13 27 49 58 76 65  
排序前: 17  | 17 28 11 36 13 27  //左子序列的第一个记录17作为枢纽，进行快排
排序后: 17  | 13 11 17 36 28 27
排序前: 13  | 13 11  //左子序列的左子序列快排
排序后: 13  | 11 13
排序前: 36  | 36 28 27  //左子序列的右子序列快排
排序后: 36  | 27 28 36
排序前: 27  | 27 28  //左子序列的右子序列的右子序列快排
排序后: 27  | 27 28
排序前: 58  | 58 76 65  //右子序列快排
排序后: 58  | 58 76 65
排序前: 76  | 76 65  //右子序列的右子序列快排
排序后: 76  | 65 76

算法分析

• 快速排序是 不稳定 的排序算法
• 时间复杂度：平均 $O(nlo{g}_{2}n)$
• 空间复杂度：需要栈的附加空间，栈平均深度 $O(lo{g}_{2}n)$
• 快速排序是所有同量级O(nlog₂n)的排序方法中，平均性能最好的

算法改进

• 若待排记录的初始状态为按关键字有序时，快速排序，将退化为起泡排序，其时间复杂度为O(n²)
  为避免出现这种情况，需在进行一次划分之前，进行“预处理”，即：先对 R(low).key, R(high).key 和 R[(low+high)/2].key，进行比较，然后取关键字为 “三者之中” 的记录作为枢轴记录

简单选择排序 略

略

9.4 堆排序

堆排序的来源

• 利用选择排序已经发生过的比较，记住比较的结果，减少重复比较次数

小根堆 大根堆

n个元素的关键字序列 R[1].key, R[2].key, … ,R[n].key
写成完全二叉树结构时，若根为R[i].key，则 左子树为R[2*i].key，右子树为R[2*i+1].key

• 小根堆：根比左子树和右子树都小（R[i].key ≤ R[2*i].key && R[i].key ≤ R[2*i+1].key）
  

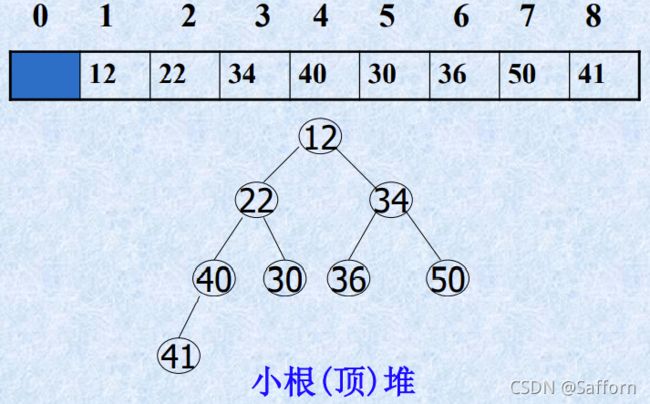
• 大根堆：根比左子树和右子树都大（R[i].key ≥ R[2*i].key && R[i].key ≥ R[2*i+1].key）
  

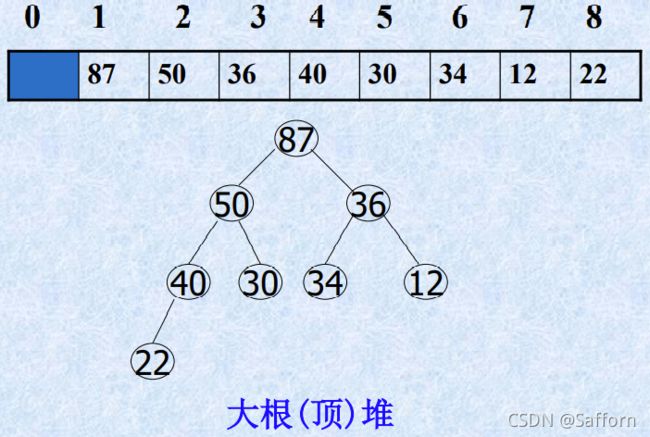
堆排序的思想

• 由无序序列建成一个堆（大根堆/小根堆）
• 输出堆顶元素后，调整剩余元素后成为一个新的堆

void HeapAdjust(int s, int m) {
    int j;
    arr[0] = arr[s];  //暂存堆顶到arr[0]
    for (j = 2 * s; j <= m; j *= 2) {
        if (j < m && arr[j] < arr[j + 1]) ++j;  //横比 j最初指向左子树
        if (arr[0] >= arr[j]) break;  //纵比 定位
        arr[s] = arr[j]; s = j;
    }
    arr[s] = arr[0];  //将调整前的堆顶记录插到位置s处
}
void HeapSort() {
    int i, temp;
    for (i = len / 2; i > 0; --i)  //建堆
        HeapAdjust(i, len);
    for (i = len; i > 1; --i) {
        temp = arr[i];
        arr[i] = arr[1];
        arr[1] = temp;
        HeapAdjust(1, i - 1);
    }
}

算法分析

• 堆排序是 不稳定 的排序算法
• 时间复杂度：$O(nlo{g}_{2}n)$
• 空间复杂度：$O(1)$

9.5 归并排序

• 归并（合并）：把两个及以上的有序序列合并成一个有序序列

2-路归并排序

算法思想

• 把长度为 n 的序列看作 n 个长度为1的有序子序列，两两归并，得到长度为 2 或 1 的有序子序列，再两两归并… 最终得到一个长度为 n 的有序序列

算法分析
对长度为 n 的记录进行2-路归并排序

• 归并排序是 稳定 的排序方法
• 时间复杂度：$O(nlo{g}_{2}n)$，每一趟归并时间复杂度为 $O(n)$，需要进行 $lo{g}_{2}n$ 趟
• 空间复杂度：$O(n)$，借助辅助空间

k-路归并排序需要进行 $lo{g}_{k}n$ 趟，时间复杂度 $O(nlo{g}_{k}n)$

9.6 基数排序

9.7 排序方法比较

排序趟数与序列的原始状态有关的排序方法是 冒泡、快速

• 插入排序

  • 在最后一趟开始之前，可能所有元素都不在其最终的位置上
  • 对初始状态为递增序列的表按递增顺序排序，最省时间

• 快速排序

  • 排序趟数与序列的原始状态有关
  • 对初始状态为递增序列的表按递增顺序排序，最费时间

• 堆排序

  • 可以直接得出指定范围的局部有序结果，例如取1000个中的最大10个

• 归并排序（2-路归并）

  • 在一趟结束后不一定能选出一个元素放在其最终位置上
  • 尽可能快地进行稳定的排序
  • 将两个长度分别为n，m的递增有序顺序表归并成一个有序顺序表，其元素最多的比较次数是 m+n-1