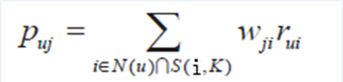算法篇--协同过滤
文章目录
-
-
- 一、长尾理论
- 二、协同过滤介绍
- 三、相似度度量方法
-
- 1. 杰卡德(Jaccard)相似系数
- 2. 余弦相似度
- 3. 皮尔逊相关系数
- 四、基于用户的协同过滤算法(User-based CF,简称UserCF)
- 五、基于物品的协同过滤算法(Item-based CF,简称ItemCF)
-
- 第一步:计算物品之间的相似度;
- 第二步:根据物品的相似度和用户的历史行为给用户生成推荐列表;
- 六、算法评估
-
- 1. 召回率
- 2. 准确率
- 3. 覆盖率
- 4. 新颖度
- 七、协同过滤算法的问题分析
-
- 1. 数据稀疏性的问题
- 2. 扩展性问题
- 3. 泛化能力弱的问题
- 4. 冷启动问题
-
- (1)介绍:
- (2)用户冷启动:
- (3)物品冷启动:
- 5. 其它一些问题和挑战
- 八、总结
-
一、长尾理论
wiki链接:https://wiki.mbalib.com/wiki/%E9%95%BF%E5%B0%BE%E7%90%86%E8%AE%BA
长尾头部的商品往往代表了绝大多数用户的需求而长尾中的商品往往代表了一小部分用户的个性化需求。因此如果要通过发掘长尾来提高销售额就必须充分研究用户的个性化兴趣。而这正是个性化推荐系统主要解决的问题。
推荐系统通过发掘用户的行为找到用户的个性化需求从而将长尾中的商品准确地推荐给需要它们的用户帮助用户发现那些他们感兴趣但很难发现的商品。
解释了“长尾效应”,接下来就要开始进入推荐系统真正的核心内容——推荐算法。如今大部门电子商务或者社交网站的推荐引擎用到的工作原理是基于物品或者用户的相似集合进行推荐。而主流的推荐算法模型仍旧是基于协同过滤来完成推荐。可以这么说,目前市面上超过半成的推荐系统仍旧依靠的是协同过滤算法,并且整体推荐效果不亚于新研究出来的其他推荐算法,并且协同过滤推荐算法的性能最为稳定,只要提到推荐系统,第一个出现在我们脑海里的算法就是协同过滤。所以,不得不说协同过滤算法是经典的、不过时的。(本段话来自:推荐算法集锦(上)——协同过滤算法)
二、协同过滤介绍
协同过滤(英语:Collaborative Filtering),简单来说是利用某兴趣相投、拥有共同经验之群体的喜好来推荐用户感兴趣的信息,个人通过合作的机制给予信息相当程度的回应(如评分)并记录下来以达到过滤的目的进而帮助别人筛选信息,回应不一定局限于特别感兴趣的,特别不感兴趣信息的纪录也相当重要。协同过滤又可分为评比(rating)或者群体过滤(social filtering)。(本段来自维基百科),发展历史可参考协同过滤和推荐算法集锦(上)——协同过滤算法中的部分内容
协同过滤(Collaborative Filtering,简称CF)是一种流行的推荐算法,其基于系统中其他用户的评分或行为进行预测和推荐。就是指用户可以齐心协力,通过不断地和网站互动,使自己的推荐列表能够不断过滤掉自己不感兴趣的物品,从而越来越满足自己的需求。
显性反馈:用户明确表示对物品喜好的行为。主要方式是评分和喜欢/不喜欢。
隐形反馈:不能明确反应用户喜好的行为。(购买日志、阅读日志、浏览日志)
目前应用比较广泛的协同过滤算法是基于邻域的方法, 而这种方法主要有下面两种算法:
- 基于用户的协同过滤算法(UserCF): 给用户推荐和他兴趣相似的其他用户喜欢的产品
- 基于物品的协同过滤算法(ItemCF): 给用户推荐和他之前喜欢的物品相似的物品
协同过滤的核心是构建用户物品的评分矩阵,这个矩阵是稀疏的,因为用户不可能对所有的物品进行评价。向量维度上的取值可以是简单的 0 或者 1,也可以是1,2,3,4,5这种评分数据。以下是两种典型的稀疏矩阵存储格式:
- CSR:这个存储稍微复杂点,是一个整体编码方式。它有三个组成:数值、列号和行偏移共同编码。
- COO:这个存储方式很简单,每个元素用一个三元组表示(行号,列号, 数值),只存储有值的元素,缺失值不存储。
这些存储格式,在常见的计算框架里面都是标准的,如 Spark 中,Python 的 NumPy 包中。一些著名的算法比赛也通常都是以这种格式提供数据。把原始行为日志转换成上面的格式,就可以使用常用计算框架的标准输入了。(来自:推荐系统组队学习——协同过滤)
三、相似度度量方法
1. 杰卡德(Jaccard)相似系数
两个用户 u 和 v 交互商品交集的数量占这两个用户交互商品并集的数量的比例,称为两个集合的杰卡德相似系数,用符号 sim 表示,其中 N(u),N(v)分别表示用户 u 和用户 v 交互商品的集合。

由于杰卡德相似系数一般无法反映具体用户的评分喜好信息, 所以常用来评估用户是否会对某商品进行打分, 而不是预估用户会对某商品打多少分。(这句话的准确性有待考证)

2. 余弦相似度
余弦相似度衡量了两个向量的夹角,夹角越小越相似。首先从集合的角度描述余弦相似度,相比于Jaccard公式来说就是分母有差异,不是两个用户交互商品的并集的数量,而是两个用户分别交互的商品数量的乘积,公式如下:

从向量的角度进行描述,令矩阵 A 为用户-商品交互矩阵(因为是TopN推荐并不需要用户对物品的评分,只需要知道用户对商品是否有交互就行),即矩阵的每一行表示一个用户对所有商品的交互情况,有交互的商品值为1没有交互的商品值为0,矩阵的列表示所有商品。若用户和商品数量分别为 m,n的话,交互矩阵 就是一个 m 行 n 列的矩阵。此时用户的相似度可以表示为(其中 u*v 指的是向量点积):

为了避免存储这么大的稀疏矩阵,在计算用户相似度的时候一般会采用集合的方式进行计算。理论上向量之间的相似度计算公式都可以用来计算用户之间的相似度,但是会根据实际的情况选择不同的用户相似度度量方法。
from sklearn.metrics.pairwise import cosine_similarity
i = [1, 0, 0, 0]
j = [1, 0.5, 0.5, 0]
consine_similarity([a, b])
3. 皮尔逊相关系数
皮尔逊相关系数的公式与余弦相似度的计算公式非常的类似,首先对于上述的余弦相似度的计算公式写成求和的形式,其中rui ,rvi分别表示用户 u 和用户 v 对商品 i 是否有交互(或者具体的评分值):

如下是皮尔逊相关系数计算公式,减去了用户 u 和用户 v 交互的所有商品交互数量或者具体评分的平均值。

相比余弦相似度,皮尔逊相关系数通过使用用户的平均分对各独立评分进行修正,减小了用户评分偏置的影响。
from scipy.stats import pearsonr
i = [1, 0, 0, 0]
j = [1, 0.5, 0.5, 0]
pearsonr(i, j)
四、基于用户的协同过滤算法(User-based CF,简称UserCF)
参考:推荐系统实践–基于用户的协同过滤算法
每年新学期开始,刚进实验室的师弟总会问师兄相似的问题,比如“我应该买什么专业书啊”、“我应该看什么论文啊”等。这个时候,师兄一般会给他们做出一些推荐。这就是现实中个性化推荐的一种例子。在这个例子中,师弟可能会请教很多师兄,然后做出最终的判断。师弟之所以请教师兄,一方面是因为他们有社会关系,互相认识且信任对方,但更主要的原因是师兄和师弟有共同的研究领域和兴趣。那么,在一个在线个性化推荐系统中,当一个用户A需要个性化推荐时,可以先找到和他有相似兴趣的其他用户,然后把那些用户喜欢的、而用户A没有听说过的物品推荐给A。这种方法称为基于用户的协同过滤算法。
算法核心:当一个用户A需要个性化推荐时,可以先找到他有相似兴趣的其他用户,然后把那些用户喜欢的、而用户A没听过的物品推荐给A。UserCF算法主要包括两个步骤:
- 找到和目标用户兴趣相似的用户集合。
- 找到这个集合中的用户喜欢的,且目标用户没有听说过的物品推荐给目标用户。
步骤一的关键就是计算两个用户的兴趣相似度。这里,协同过滤算法主要利用行为的相似度计算兴趣的相似度。给定用户u和用户v,令N(u)表示用户u曾经有过正反馈的物品集合,令N(v)为用户v曾经有过正反馈的物品集合。那么,我们可以通过如下的杰卡德(Jaccard)公式简单地计算u和v的兴趣相似度或者通过余弦公式:
Jaccard:

余弦公式:

这是一个行为记录我们可以根据余弦公式计算如下:
def UserSimilarity(train):
W = dict()
for u in train.keys():
for v in train.keys():
if u == v:
continue
W[u][v] = len(train[u] & train[v])
W[u][v] = /= math.sqrt(len(train[u]) * len(train[v]) * 1.0)
return W
这种方法的时间复杂度是O(|U|*|U|),这在用户数很大时非常耗时。事实上,很多用户相互之间并没有对同样的物品产生过行为,即很多时候N(u)^ N(v) = 0。上面的算法将很多时间浪费在了计算这种用户之间的相似度上。如果换一个思路,我们可以首先计算出N(u)^ N(v) != 0 的用户对(u,v),然后再对这种情况除以分母sqrt(N(u)*N(v)) 。
为此,可以首先建立物品到用户的倒排表,对于每个物品都保存对该物品产生过行为的用户列表。令稀疏矩阵C[u][v]= N(u)^ N(v) 。那么,假设用户u和用户v同时属于倒排表中K个物品对应的用户列表,就有C[u][v]=K。从而,可以扫描倒排表中每个物品对应的用户列表,将用户列表中的两两用户对应的C[u][v]加1,最终就可以得到所有用户之间不为0的C[u][v]
def UserSimilarity(train):
# build inverse table for item_users
item_users = dict()
for u, items in train.items():
for i in items.keys():
if i not in item_users:
item_users[i] = set()
item_users[i].add(u)
#calculate co-rated items between users
C = dict()
N = dict()
for i, users in item_users.items():
for u in users:
N[u] += 1
for v in users:
if u == v:
continue
C[u][v] += 1
#calculate finial similarity matrix W
W = dict()
for u, related_users in C.items():
for v, cuv in related_users.items():
W[u][v] = cuv / math.sqrt(N[u] * N[v])
return W
下面是按照想法建立的稀疏矩阵,对于物品a,将W[A][B]和W[B][A]加1,对于物品b,将W[A][C]和W[C][A]加1,以此类推,扫描完所有物品后,我们可以得到最终的W矩阵,这里的W是余弦相似度中的分子部分,然后将W除以分母可以得到最终的用户兴趣相似度。

计算u对物品i的感兴趣程序:

得到用户之间的兴趣相似度后,UserCF算法会给用户推荐和他兴趣最相似的K个用户喜欢的物品。上面右边公式度量了UserCF算法中用户u对物品i的感兴趣程度:其中,S(u, K)包含和用户u兴趣最接近的K个用户,N(i)是对物品i有过行为的用户集合,Wuv是用户u和用户v的兴趣相似度,Rvi代表用户v对物品i的兴趣,因为使用的是单一行为的隐反馈数据,所以所有的Rvi=1。
如下代码实现了上面的UserCF推荐算法:
def Recommend(user, train, W):
rank = dict()
interacted_items = train[user]
for v, wuv in sorted(W[u].items, key=itemgetter(1), reverse=True)[0:K]:
for i, rvi in train[v].items:
if i in interacted_items:
#we should filter items user interacted before
continue
rank[i] += wuv * rvi
return rank
选取K=3,用户A对物品c、e没有过行为,因此可以把这两个物品推荐给用户A。根据UserCF算法,用户A对物品c、e的兴趣是:

如果两个用户都曾经买过《新华字典》,这丝毫不能说明他们兴趣相似,因为绝大多数中国人小时候都买过《新华字典》。但如果两个用户都买过《数据挖掘导论》,那可以认为他们的兴趣比较相似,因为只有研究数据挖掘的人才会买这本书。换句话说,两个用户对冷门物品采取过同样的行为更能说明他们兴趣的相似度。因此,John S. Breese在论文①中提出了如下公式,根据用户行为计算用户的兴趣相似度:

分子中的倒数惩罚了用户u和用户v共同兴趣列表中热门物品对他们相似度的影响。N(i)是对物品i有过行为的用户集合,越热门,N(i)越大
def UserSimilarity(train):
# build inverse table for item_users
item_users = dict()
for u, items in train.items():
for i in items.keys():
if i not in item_users:
item_users[i] = set()
item_users[i].add(u)
#calculate co-rated items between users
C = dict()
N = dict()
for i, users in item_users.items():
for u in users:
N[u] += 1
for v in users:
if u == v:
continue
C[u][v] += 1 / math.log(1 + len(users))
#calculate finial similarity matrix W
W = dict()
for u, related_users in C.items():
for v, cuv in related_users.items():
W[u][v] = cuv / math.sqrt(N[u] * N[v])
return W
基于用户的协同过滤算法存在两个重大问题:
- 数据稀疏性: 一个大型的电子商务推荐系统一般有非常多的物品,用户可能买的其中不到1%的物品,不同用户之间买的物品重叠性较低,导致算法无法找到一个用户的邻居,即偏好相似的用户。这导致UserCF不适用于那些正反馈获取较困难的应用场景(如酒店预订, 大件商品购买等低频应用)
- 算法扩展性:基于用户的协同过滤需要维护用户相似度矩阵以便快速的找出Topn相似用户, 该矩阵的存储开销非常大,存储空间随着用户数量的增加而增加,不适合用户数据量大的情况使用。
由于UserCF技术上的两点缺陷, 导致很多电商平台并没有采用这种算法, 而是采用了ItemCF算法实现最初的推荐系统。
参考:推荐系统组队学习——协同过滤)
针对向量很长的问题,有两个解决办法:
- 对向量采样计算,即从高维向量中随机取几维进行计算相似度,这个算法由 Twitter 提出,叫做 DIMSUM 算法,已经在 Spark 中实现了。
- 向量化计算,想办法把循环转换成向量来直接计算,比如 Python 的 NumPy 。
针对用户量很大的问题,解决办法如下:
- 将相似度计算拆成 Map Reduce 任务,将原始矩阵 Map 成键为用户对,值为两个用户对同一个物品的评分之积,Reduce 阶段对这些乘积再求和,Map Reduce 任务结束后再对这些值归一化
- 不用基于用户的协同过滤
五、基于物品的协同过滤算法(Item-based CF,简称ItemCF)
参考:推荐算法–基于物品的协同过滤算法
算法核心思想:给用户推荐那些和他们之前喜欢的物品相似的物品。
基于物品的协同过滤算法主要分为两步:
- 计算物品之间的相似度;
- 根据物品的相似度和用户的历史行为给用户生成推荐列表;
下面分别来看这两步如何计算:
第一步:计算物品之间的相似度;
我们使用下面的公式定义物品的相似度:

其中,|N(i)|是喜欢物品i的用户数,|N(j)|是喜欢物品j的用户数,|N(i)&N(j)|是同时喜欢物品i和物品j的用户数。
从上面的定义看出,在协同过滤中两个物品产生相似度是因为它们共同被很多用户喜欢,两个物品相似度越高,说明这两个物品共同被很多人喜欢。
这里面蕴含着一个假设:就是假设每个用户的兴趣都局限在某几个方面,因此如果两个物品属于一个用户的兴趣列表,那么这两个物品可能就属于有限的几个领域,而如果两个物品属于很多用户的兴趣列表,那么它们就可能属于同一个领域,因而有很大的相似度。(用户活跃度大的用户可能喜欢列表中有很多商品,会影响ItemCf算法计算结果准确性,后面优化算法会增加一个用户活跃度分子)
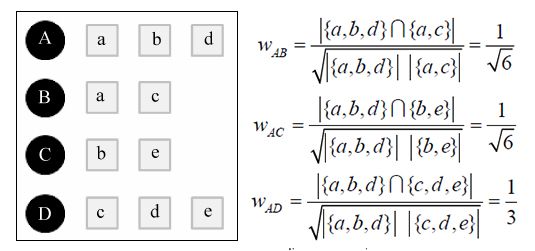
举例,用户A对物品a、b、d有过行为,用户B对物品b、c、e有过行为,等等;

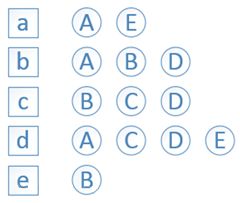
依此构建用户——物品倒排表:物品a被用户A、E有过行为,等等;

其中,C[i][j]记录了同时喜欢物品i和物品j的用户数,这样我们就可以得到物品之间的相似度矩阵W。在得到物品之间的相似度后,进入第二步。
第二步:根据物品的相似度和用户的历史行为给用户生成推荐列表;
ItemCF通过如下公式计算用户u对一个物品j的兴趣:
其中,Puj表示用户u对物品j的兴趣,N(u)表示用户喜欢的物品集合(i是该用户喜欢的某一个物品),S(i,k)表示和物品i最相似的K个物品集合(j是这个集合中的某一个物品),Wji表示物品j和物品i的相似度,Rui表示用户u对物品i的兴趣(这里简化Rui都等于1)。
该公式的含义是:和用户历史上感兴趣的物品越相似的物品,越有可能在用户的推荐列表中获得比较高的排名。
下面是一个书中的例子(项亮的 《推荐系统》一书),帮助理解ItemCF过程:
有两种推荐场景:(来自:推荐系统组队学习——协同过滤))
- Top-k推荐:要预测一个用户 u 对一个物品 i 的分数,遍历用户 u 评分过的所有物品,假如一共有 m 个,每一个物品和待计算物品 i 的相似度乘以用户的评分,这样加权求和后,除以所有这些相似度总和,就得到了一个加权平均评分,作为用户 u 对物品 i 的分数预测。
这个过程都是离线完成后,去掉那些用户已经消费过的,保留分数最高的 k 个结果存储。当用户访问首页时,直接查询出来即可。
- 相关推荐:这类推荐不需要提前合并计算,当用户访问一个物品的详情页面时,或者完成 一个物品消费的结果面,直接获取这个物品的相似物品推荐。
SlopeOne 算法 :经典的基于物品推荐,相似度矩阵计算无法实时更新。因此我们计算物品之间的距离,最后按照加权即可得到结果。
编程实现:
"""计算物品的相似矩阵"""
similarity_matrix = pd.DataFrame(np.ones((len(items), len(items))), index=['A', 'B', 'C', 'D', 'E'], columns=['A', 'B', 'C', 'D', 'E'])
# 遍历每条物品-用户评分数据
for itemId in items:
for otheritemId in items:
vec_item = [] # 定义列表, 保存当前两个物品的向量值
vec_otheritem = []
#userRagingPairCount = 0 # 两件物品均评过分的用户数
if itemId != otheritemId: # 物品不同
for userId in users: # 遍历用户-物品评分数据
userRatings = users[userId] # 每条数据为该用户对所有物品的评分, 这也是个字典
if itemId in userRatings and otheritemId in userRatings: # 用户对这两个物品都评过分
#userRagingPairCount += 1
vec_item.append(userRatings[itemId])
vec_otheritem.append(userRatings[otheritemId])
# 这里可以获得相似性矩阵(共现矩阵)
similarity_matrix[itemId][otheritemId] = np.corrcoef(np.array(vec_item), np.array(vec_otheritem))[0][1]
#similarity_matrix[itemId][otheritemId] = cosine_similarity(np.array(vec_item), np.array(vec_otheritem))[0][1]
"""得到与物品5相似的前n个物品"""
n = 2
similarity_items = similarity_matrix['E'].sort_values(ascending=False)[:n].index.tolist() # ['A', 'D']
"""计算最终得分"""
base_score = np.mean(np.array([value for value in items['E'].values()]))
weighted_scores = 0.
corr_values_sum = 0.
for item in similarity_items: # ['A', 'D']
corr_value = similarity_matrix['E'][item] # 两个物品之间的相似性
mean_item_score = np.mean(np.array([value for value in items[item].values()])) # 每个物品的打分平均值
weighted_scores += corr_value * (users[1][item]-mean_item_score) # 加权分数
corr_values_sum += corr_value
final_scores = base_score + weighted_scores / corr_values_sum
print('用户Alice对物品5的打分: ', final_scores)
user_df.loc[1]['E'] = final_scores
user_df
下面是书中提到的几个优化方法:
(1)用户活跃度对物品相似度的影响
即认为活跃用户对物品相似度的贡献应该小于不活跃的用户,所以增加一个IUF(Inverse User Frequence)参数来修正物品相似度的计算公式:
用这种相似度计算的ItemCF被记为ItemCF-IUF。
ItemCF-IUF在准确率和召回率两个指标上和ItemCF相近,但它明显提高了推荐结果的覆盖率,降低了推荐结果的流行度,从这个意义上说,ItemCF-IUF确实改进了ItemCF的综合性能。
(2)物品相似度的归一化
Karypis在研究中发现如果将ItemCF的相似度矩阵按最大值归一化,可以提高推荐的准确度。其研究表明,如果已经得到了物品相似度矩阵w,那么可用如下公式得到归一化之后的相似度矩阵w’:

最终结果表明,归一化的好处不仅仅在于增加推荐的准确度,它还可以提高推荐的覆盖率和多样性。
用这种相似度计算的ItemCF被记为ItemCF-Norm。
六、算法评估
1. 召回率
对用户u推荐N个物品记为 R(u), 令用户u在测试集上喜欢的物品集合为 T(u), 那么召回率定义为:

在用户真实购买的影片里面, 模型真正预测出了多少, 考察的是模型推荐的全面性。
2. 准确率

在推荐的所有物品中, 用户真正看的有多少, 这个考察的是模型推荐的准确性。为了提高准确率, 模型需要把非常有把握的才对用户进行推荐, 所以这时候就减少了推荐数量, 而这往往损失了全面性, 真正预测出来的会非常少,所以实际应用中应该综合考虑两者的平衡。
来自:准确率、精确率、召回率、F1值
下面我们通过一个简单例子来看看精确率和召回率。假设一共有10篇文章,里面4篇是你要找的。根据你的算法模型,你找到了5篇,但实际上在这5篇之中,只有3篇是你真正要找的。
那么算法的精确率是3/5=60%,也就是你找的这5篇,有3篇是真正对的。算法的召回率是3/4=75%,也就是需要找的4篇文章,你找到了其中三篇。以精确率还是以召回率作为评价指标,需要根据具体问题而定。
3. 覆盖率
覆盖率反映了推荐算法发掘长尾的能力, 覆盖率越高, 说明推荐算法越能将长尾中的物品推荐给用户。

该覆盖率表示最终的推荐列表中包含多大比例的物品。如果所有物品都被给推荐给至少一个用户, 那么覆盖率是100%。
4. 新颖度
用推荐列表中物品的平均流行度度量推荐结果的新颖度。 如果推荐出的物品都很热门, 说明推荐的新颖度较低。 由于物品的流行度分布呈长尾分布, 所以为了流行度的平均值更加稳定, 在计算平均流行度时对每个物品的流行度取对数。
七、协同过滤算法的问题分析
1. 数据稀疏性的问题
推荐系统面临的问题中最大的问题就是数据稀疏性问题,它会影响推荐系统推荐的准确度,在个性化推荐系统中,协同过滤是最常用的技术,数据稀疏性影响了协同过滤的结果,因为在很多推荐系统中只有很小一部分评分,当在评分很小的情况下,推荐的准确度也会下降。
目前来说解决数据稀疏问题最好的算法是降维技术,比如奇异值SVD分解。降维技术的关键是通过原始矩阵通过计算来求其低维度的相似来降低矩阵的维度,有一点弊端就是数据量大的时候运算成本很高,好在最近几年云计算发展迅猛,这些计算量都可以放在运动,来弥补计算量的问题,除了降维技术之外人口统计过滤也是解决数据稀疏性问题的很好的方法,人口统计过滤是通过用户资料的对比找到用户相似,然后通过相似的用户来进行推荐,这种方式可以解决数据量很稀疏的情况下使用。
2. 扩展性问题
推荐系统中通过推荐算法获得之后,因为用户之前没有足够多的对物品进行评分,有时候很难掌握用户的各方面兴趣和需求,这就会导致出现过拟合现象,这一类现象就是推荐系统中的扩展性问题,这类问题对于推荐系统的体验上是一个很大的问题。
扩展性问题在实际应用中是无可避免的,其中受数据集大小的扩展,数据完整性等问题的限制,对于数据完整性的问题,通常是引入随机性,使算法收敛到全局最优或者逼近全局最优,但是推荐系统运行过程是动态变化的,同时也会受冷启动影响,用户/对象/喜好数据达到一定规模时,性能这个时候也会存在一些瓶颈,这个时候的大数据处理和算法的可扩展性成为推荐算法技术需要实施并迫切需要解决的问题。
3. 泛化能力弱的问题
协同过滤算法存在的问题之一就是泛化能力弱, 即协同过滤无法将两个物品相似的信息推广到其他物品的相似性上。 导致的问题是热门物品具有很强的头部效应, 容易跟大量物品产生相似, 而尾部物品由于特征向量稀疏, 导致很少被推荐。 比如下面这个例子:

A, B, C, D是物品, 看右边的物品共现矩阵, 可以发现物品D与A、B、C的相似度比较大, 所以很有可能将D推荐给用过A、B、C的用户。 但是物品D与其他物品相似的原因是因为D是一件热门商品, 系统无法找出A、B、C之间相似性的原因是其特征太稀疏, 缺乏相似性计算的直接数据。 所以这就是协同过滤的天然缺陷:推荐系统头部效应明显, 处理稀疏向量的能力弱。
为了解决这个问题, 同时增加模型的泛化能力,2006年,矩阵分解技术(Matrix Factorization,MF)被提出, 该方法在协同过滤共现矩阵的基础上, 使用更稠密的隐向量表示用户和物品, 挖掘用户和物品的隐含兴趣和隐含特征, 在一定程度上弥补协同过滤模型处理稀疏矩阵能力不足的问题。
4. 冷启动问题
参考:推荐系统实战-冷启动问题
(1)介绍:
如何在没有大量用户数据的情况下设计个性化推荐系统并让用户对推荐结果满意从而愿意使用推荐系统,就是冷启动问题:
- 用户冷启动:如何给新用户做个性化推荐
- 物品冷启动:如何将新物品推荐给可能对其感兴趣的用户。在新闻网站等时效性很强的网站中非常重要。
- 系统冷启动:如何在一个新开发的网站上设计个性化推荐,从而在网站刚发布时就让用户体验到个性化推荐服务。没有用户,只有一些物品信息。
解决冷启动问题方法概述:
- 提供非个性化的推荐
- 利用用户注册时提供的年龄、性别等数据做粗粒度的个性化。
- 利用社交账号登录(需要用户授权),导入用户在社交网络上的好友信息,然后给用户推荐其好友喜欢的物品。
- 要求用户在登录时对一些物品进行反馈,搜集用户对这些物品的兴趣信息,然后给用户推荐那些和这些物品相似的物品。
- 对于新加入的物品,可以利用内容信息,将它们推荐给喜欢过和他们相似物品的用户。(没有购买记录,如何判断物品相似)
- 推荐系统冷启动时,引入专家的知识,通过一定的高效方式迅速建立起物品的相关度表。
(2)用户冷启动:
用户注册时附带信息:
- 人口统计学信息:包括用户的年龄、性别、职业、民族、学历和居住地;
- 用户兴趣的描述:有一些网站会让用户用文字或用区域选择来描述他们的兴趣;
- 从其他网站导入的用户站外行为数据:比如用户通过豆瓣、新浪微博的账号登录,就可以在得到用户同意的情况下获取用户在豆瓣或者新浪微博的一些行为数据和社交网络数据。
基于注册信息的个性化推荐流程基本如下:
- 获取用户的注册信息;
- 根据用户的注册信息对用户分类;
- 给用户推荐他所属分类中用户喜欢的物品;
- 若无法找到合适的物品,推荐热门排行榜。
注:该方法中需要统计物品对分类的热门程度,通过如下公式:P(f,i) = |N(i) ∩ U(f)| (其中N(i)是喜欢物品的用户集合,U(f) 是具有某种特征的用户集合),这种方法对热门商品的热门程度往往比较大,在分母中增加一项: |N(i) + α|
选择合适的物品启动用户的兴趣:解决用户冷启动问题的另一个方法是在新用户第一次访问推荐系统时,不立即给用户展示推荐结果,而是给用户提供一些物品,让用户反馈他们对这些物品的兴趣,然后根据用户反馈给提供个性化推荐。
一般来说,能够用来启动用户兴趣的物品需要具有以下特点:
- 比较热门。如果要让用户对一个物品进行反馈,前提是用户知道这个物品是什么东西;
- 具有代表性和区分性。启动用户兴趣的物品不能是大众化或老少咸宜的,因为这样的物品对用户的兴趣没有区分性;
- 启动物品集合需要有多样性。在冷启动时,我们不知道用户的兴趣,而用户兴趣的可能性非常多,为了匹配多样的兴趣,我们需要提供具有很高覆盖率的启动物品集合,这些物品能覆盖几乎所有主流的用户兴趣。

(3)物品冷启动:
物品冷启动需要解决的问题是如何将新加入的物品推荐给对它感兴趣的用户,这时候可以通过物品之间的语义来计算其相似度,常用的算法有cos相似度和TF-IDF。
物品冷启动在新闻网站等时效性很强的网站中非常重要,因为那些网站中时时刻刻都有新加入的物品,而且每个物品必须能够在第一时间展现给用户,否则经过一段时间后,物品的价值就大大降低了。
之前我们介绍了UserCF算法和ItemCF算法。UserCF算法并不对新物品很敏感,在很多网站中,推荐列表并不是给用户展示物品的唯一列表。当一个用户在某个地方发现了新加的物品并对其进行了反馈。通过UserCF算法给类似具有相同兴趣的用户推荐这个物品。这样新加的物品就会源源不断的扩散开来。
但是有些网站中推荐列表就是用户获取新加物品唯一的或者是主要途径。这时就要解决第一推动力的问题。也即是第一个用户在哪发现新加物品的问题。解决这个问题的最简单的办法就是将新加的物品随机的展示给用户,但是这样做显然并不个性化。因此可以考虑利用物品内容信息,将新物品投放给曾经喜欢过和他类似内容的其他物品的用户,这类似于ItemCF思想。不过这是先通过ItemCF找到一个可能对物品感兴趣的用户,然后再通过USerCF推荐给与此用户兴趣类似的其他用户。
如果用ItemCF算法解决物品冷启动问题,就有点麻烦了,因为ItemCF通过用户行为对物品进行相似度的计算,形成物品相似度矩阵。再根据这个相似度矩阵把物品推荐给喜欢过类似这个物品的用户。这个物品相似度矩阵是线下计算好,线上放进内存。从而新物品不会出现在物品相似度矩阵中。解决的办法是频繁的更新相似度矩阵。这是一件非常耗时的事情。为此我们只能通过物品内容来计算物品相似度矩阵。
这里涉及到物品相似度的计算,和ItemCf中物品相似度计算不同的是,对于新物品这里并没有用户数据,所以一般通过物品内容计算相似度。
一般来说,物品的内容可以用向量空间模型表示,该模型会把物品表示成一个关键词向量。对于物品d,他的内容表示成一个关键词向量如下: 其中e是关键词,w是这个词对于权重,其中w的计算公式就是著名的TF-IDF公式,该公式的计算见后文中具体介绍
![]()
在给定物品内容的关键词向量后,物品内容响度可以通过向量之间的余弦相似度计算:

《推荐系统实战》中具体比较了内容过滤算法和协同过滤算法在推荐系统中的实际效果(有准确率、召回率、覆盖率等数据)。
5. 其它一些问题和挑战
推荐系统在推荐的过程中还会存在隐私问题、噪声问题、解释性问题、合理性、新颖性等等,这些问题在推荐系统中很有挑战性,但是解决这些问题出现的同时也会改变推荐准确度,所以我们需要权衡这些问题和推荐之间的联系,目前很多算法都有在改进相关的问题,改进的措施也是多维度的。
八、总结
- UserCF的适用情况:用户少, 物品多, 时效性较强的场合
- ItemCF的适用情况:物品少,用户多,用户兴趣固定持久, 物品更新速度不是太快的场合
参考:
推荐系统-协同过滤原理与实现
推荐算法三视角:矩阵,图,时间线
王小明数据分析学习笔记(六) 推荐系统随笔 HQL实现协同过滤
从零开始写一个推荐系统第二篇,推荐电影
推荐系统——2.1协同过滤