PageRank算法详解

$\mathbf{PageRank}$算法的基本想法是在有向图上定义一个随机游走模型，即一阶马尔可夫链，描述随机游走者沿着有向图随机访问各个结点的行为。在一定条件下，极限情况访问每个结点的概率收敛到平稳分布，这时各个结点的平稳概率值就是其$\mathbf{PageRank}$值，表示结点的重要度。$\mathbf{PageRank}$是递归定义的，$\mathbf{PageRank}$的计算可以通过迭代算法进行。

1、$\mathbf{PageRank}$ 基本定义

已知：一个包含$n$个节点的强连通且非周期性的有向图，在此基础上定义随机游走模型（一阶马尔科夫链）。

随机游走的特点：一个节点转移到有向边连出的所有节点的概率相等，转移矩阵为$\mathbf{M}$，并且这个马尔可夫链具有平稳分布$R$，所谓平稳分布也就是最终节点间的转移概率趋于平稳，平稳分布可以认为是一个最终收敛后得到的概率矩阵。
$$MR=R$$
此时，平稳分布 $\mathbf{R}$ 即为有向图的 $\mathbf{PageRank}$ 值，$\mathbf{R}$的各个分量为每一个节点 $v_i$ 的$\mathbf{PageRank}$值
R = [ P R ( v 1 ) P R ( v 2 ) ⋯ P R ( v i ) ] R=\begin{bmatrix} PR(v_1)\\ PR(v_2)\\\cdots \\PR(v_i) \end{bmatrix} R= ​PR(v1​)PR(v2​)⋯PR(vi​)​ ​
并且满足，
$$PR(v_i)\ge 0,i=1,2,\dots ,n$$
$$\sum _{i=1}^{n}PR(v_i)=1$$

最后得到
$$PR(v_i)=\sum _{v_j\in M(v_i)}\frac{PR(v_j)}{N(v_j)}$$
节点 $v_i$ 的$\mathbf{PageRank}$值为其连边节点$\mathbf{PageRank}$值的总和

1.1 Spider Traps问题

自循环节点。某个节点存在一个外链，并且外链连接自己

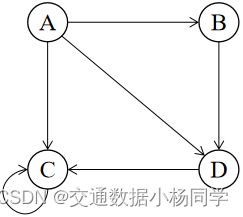
此类问题情况下，转移矩阵 $\mathbf{M}$ 如下：

可以发现节点 $\mathbf{C}$ 唯一连接是连接自己，导致转移矩阵 $\mathbf{C}$ 节点转移至其它节点的概率均为0，而C节点的$\mathbf{PageRank}$会趋于1，而其他节点的$\mathbf{PageRank}$值趋于0

Spider Traps解决方案

为了避免这种节点没有出链或只有入链的情况。在式中增加了阻尼因子，阻尼因子模拟了用户通过链接继续点击网页的概率，避免了某个节点$\mathbf{PageRank}$值趋于1的情况。

得到改进后$\mathbf{PageRank}$计算公式如下图，d为阻尼因子，N为页面总数。
$$PR(v_i)=d\mathbf{M}R+(1-d)$$
前一项表示访问节点的概率，若该节点没有访问者，则概率为$1-d$，避免了最终概率为0的情况

1.2 Dead Ends问题

一般的有向图未必满足强连通且非周期，比如在互联网中，一部分网页没有连接出去的超链接，也就是通过这些网页无法跳转到其它网页。

此类问题情况下，转移矩阵 $\mathbf{M}$ 如下：

可以发现节点 $\mathbf{C}$ 没有连出的外链，导致转移矩阵 $\mathbf{C}$ 节点转移至其它节点的概率均为$0$，会导致反复迭代之后最终结果为 $0$

Dead Ends解决方案

• 增加一个列矩阵，元素均为$\frac{1}{n}$，其中$n$为节点个数

2、$\mathbf{PageRank}$的一般定义

$\mathbf{PageRank}$的一般定义意味着互联网浏览者，按照以下方法在网上随机游走：

1. 浏览者以概率 $d$ 决定按照超链接随机跳转，这时以等概率从连接出去的超链接跳转到下一个网页
2. 以概率 $1-d$ 决定完全随机跳转，这时以等概率跳转到任意一个网页。 第二个机制保证从没有连接出去的超链接的网页也可以跳转出。

故每个节点的$\mathbf{PageRank}$值为：

P R ( v i ) = d ( ∑ v j ∈ M ( v i ) P R ( v j ) N ( v j ) ) + 1 − d n PR(v_i)=d\left ( \sum_{v_j\in M(v_i)}\frac{PR(v_j)}{N(v_j)} \right )+\frac{1-d}{n} PR(vi​)=d ​vj​∈M(vi​)∑​N(vj​)PR(vj​)​ ​+n1−d​