数据结构--顺序栈
3 栈的表示和操作的实现
3.3.1 栈的抽象数据类型的类型定义
-
InitStack(&S) 初始化操作
-
操作结果:构造一个空栈S
-
-
DestoryStack(&S) :销毁栈操作
-
初始条件:栈S已存在
-
操作结果:栈S被销毁
-
-
StackEmpty(S) 判定S是否为空栈
-
初始条件:栈S已存在
-
操作结果:若栈S为空栈,则返回TRUE,否则FALSE
-
-
StackLength(S) 求栈的长度
-
初始条件:栈S已存在
-
操作结果:返回S的元素个数,即栈的长度
-
-
GetTop(S,&e) 取栈顶元素
-
初始条件:栈S已存在且非空
-
操作结果:用e返回S的栈顶元素
-
-
ClearStack(&S) 栈置空操作
-
栈已存在
-
将S清为空栈
-
-
Push(&S,e) 入栈操作
-
初始条件:栈S已存在
-
操作结果:插入元素e为新的栈顶元素
-
-
Pop(&S,&e) 出栈操作
-
初始条件:栈S已经存在且,并用e返回其值
-
3.3.2 顺序栈的表示和实现
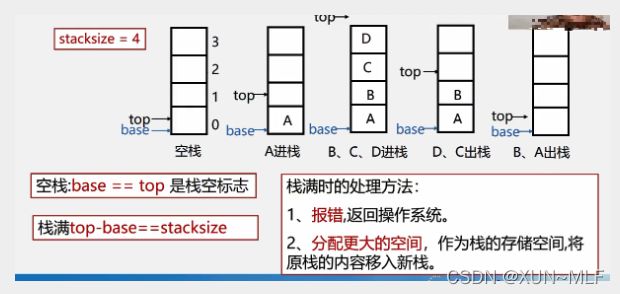
存储方式:同一般的线性表的顺序存储结构完全相同,利用一组地址连续的存储单元
依次存放自栈底到栈顶的数据元素。栈底一般在低地址端。
-
附设top指针,指示栈顶元素在顺序栈中的位置。
-
但是,为了方便操作,通常top指示真正的栈顶元素之上的下标地址。
-
-
另设base指针,指示栈底元素在顺序栈中的位置。
-
另外用stacksize表示栈可使用的最大容量。
使用数组作为顺序栈存储方式的特点:
简单,方便,但易产生溢出(数组大小固定)
-
上溢(overflow):栈已经满,又要压入元素
-
下溢(underflow):栈已经空,还要弹出元素
注:
上溢是一种错误,使问题的处理无法进行;而下溢一般认为是一种结束条件,即问题处理结束。
顺序栈的实现:
1、栈的初始化
Status InitStack(SqStack &S){
S.base = new SElemType[MAXSIZE];
if(!S.base){
return OVERFLOW;
}
S.top = S.base;
S.stacksize = MAXSIZE;
return OK;
}2、判断栈是否为空
// 2、判断栈是否为空
int StackEmpty(SqStack S){
if(S.top == S.base){
return TRUE;
}else{
return FALSE;
}
}3、求栈的长度
// 3、求栈的长度
int StackLength(SqStack S){
return S.top - S.base;
} 4、清空栈
Status StackClear(SqStack &S){
if(S.base){ // 如果栈存在
S.top = S.base;
}
return OK;
} 5、销毁栈
Status StackDestory(SqStack &S){
if(S.base){
delete S.base;
S.stacksize = 0;
S.base = S.top = NULL;
}
return OK;
} 6、压栈
// 6、压栈
Status Push(SqStack &S,SElemType e){
if(S.top-S.base == S.stacksize){ // 栈满,无法压栈
return ERROR;
}
*S.top=e;
*S.top++; // *S.top++ = e
return OK;
}7、弹栈
// 7、弹栈
Status Pop(SqStack &S,SElemType e){
if(S.top == S.base){ // 栈空,无法删除
return ERROR;
}
--S.top;
e = *S.top; // e = --*S.top;
return OK;
}
代码汇总及测试
# include
# define OK 1
# define ERROR 0
# define OVERFLOW -2
# define MAXSIZE 100
# define TRUE 1
# define FALSE 0
typedef int Status;
typedef int SElemType;
typedef struct{
SElemType *base; // 栈底指针
SElemType *top; // 栈顶指针
int stacksize; // 栈可用最大容量
}SqStack;
// 1、顺序栈的初始化
Status InitStack(SqStack &S){
S.base = new SElemType[MAXSIZE];
if(!S.base){
return OVERFLOW;
}
S.top = S.base;
S.stacksize = MAXSIZE;
return OK;
}
// 2、判断栈是否为空
int StackEmpty(SqStack S){
if(S.top == S.base){
return TRUE;
}else{
return FALSE;
}
}
// 3、求栈的长度
int StackLength(SqStack S){
return S.top - S.base;
}
// 4、清空栈
Status StackClear(SqStack &S){
if(S.base){ // 如果栈存在
S.top = S.base;
}
return OK;
}
// 5、销毁栈
Status StackDestory(SqStack &S){
if(S.base){
delete S.base;
S.stacksize = 0;
S.base = S.top = NULL;
}
return OK;
}
// 6、压栈
Status Push(SqStack &S,SElemType e){
if(S.top-S.base == S.stacksize){ // 栈满,无法压栈
return ERROR;
}
*S.top=e;
*S.top++; // *S.top++ = e
return OK;
}
// 7、弹栈
Status Pop(SqStack &S,SElemType e){
if(S.top == S.base){ // 栈空,无法删除
return ERROR;
}
--S.top;
e = *S.top; // e = --*S.top;
return OK;
}
int main(){
// 1、初始化
SqStack S;
InitStack(S);
// 2、判断是否为空
int re = StackEmpty(S);
printf("栈是否为空:%d\n",re);
// 3、压栈
Push(S,1);
Push(S,2);
// 4、栈的长度
int leng = StackLength(S);
printf("栈的长度:%d\n",leng);
// 5、弹栈
Pop(S,1);
// 4、栈的长度
int leng2 = StackLength(S);
printf("栈的长度:%d\n",leng2);
// 2、判断是否为空
int re2 = StackEmpty(S);
printf("栈是否为空:%d\n",re2);
return 0;
}