NOIP模拟赛8.15----C、三角形
C、三角形
(triangle.c/cpp/pas)
【题目描述】
平面上有n行m列,一共n*m个方格,从上到下依次标记为第1,2,...,n行,从左到右依次标记为第1,2,...,m列,方便起见,我们称第i行第j列的方格为(i,j)。小Q在方格中填满了数字,每个格子中都恰好有一个整数a_{i,j}。小Q不
喜欢手算,因此每当他不想计算时,他就会让你帮忙计算。小Q一共会给出q个询问,每次给定一个方格(x,y)和一个整数k(1<=k<=min(x,y)),你需要回答由(x,y),(x-k+1,y),(x,y-k+1)三个格子构成的三角形边上以及内部的所有
格子的a的和。
【输入格式】
第一行包含6个正整数n,m,q,A,B,C(1<=n,m<=3000,1<=q<=3000000,1<=A,B,C<=1000000)
其中n,m表示方格纸的尺寸,q表示询问个数。
为了防止输入数据过大,a和询问将由以下代码生成:
unsigned int A,B,C;
inline unsigned int rng61(){
A ^= A << 16;
A ^= A >> 5;
A ^= A << 1;
unsigned int t = A;
A = B;
B = C;
C ^= t ^ A;
return C;
}
int main(){
scanf("%d%d%d%u%u%u", &n, &m, &q, &A, &B, &C);
for(i = 1; i<= n; i++)
for(j = 1; j <= m; j++)
a[i][j] = rng61();
for(i = 1; i<= q; i++){
x = rng61() % n + 1;
y = rng61() % m + 1;
k = rng61() % min(x, y) + 1;
}
}
【输出格式】
为了防止输出数据过大,设f_i表示第i个询问的答案,则你需要输出一行一个整数,即:
输入输出样例:
| triangle.in |
triangle.out |
| 3 4 5 2 3 7
|
3350931807 |
题解
不要被那一大串代码和最后的一个式子吓到了
考场上我一开始以为要求一个任意三角形,被吓懵。。。
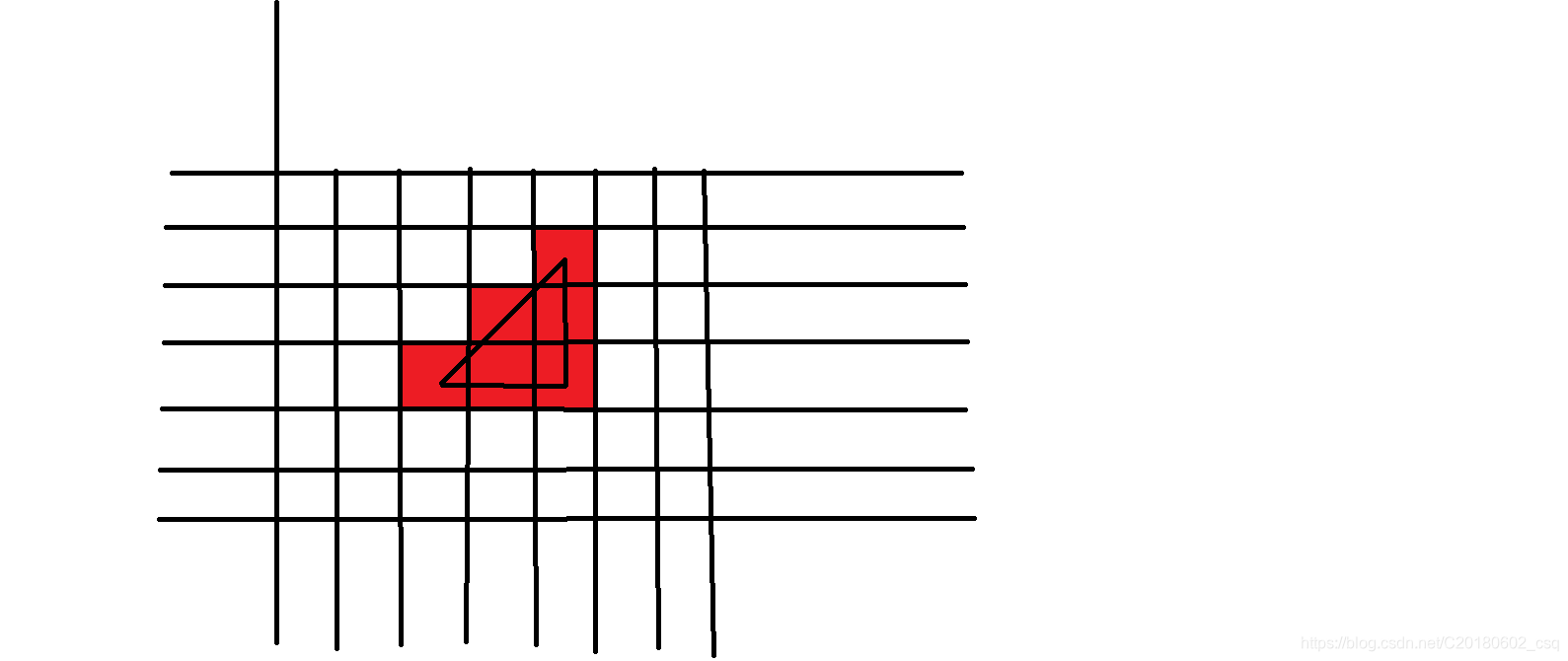
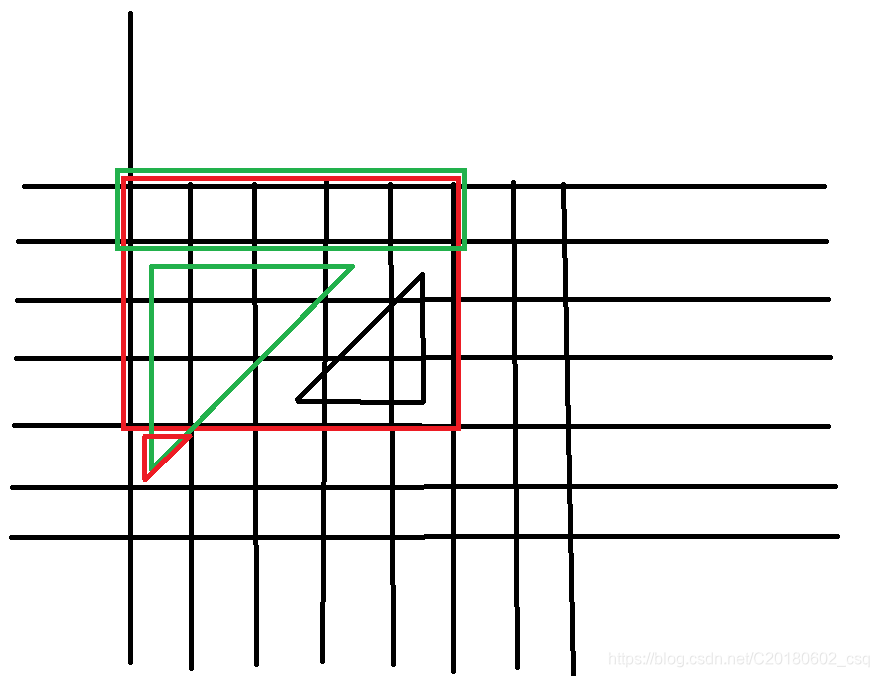
结果是求这种三角形:
于是我们可以用一些奇奇怪怪的前缀和和奇奇怪怪的加加减减来算算
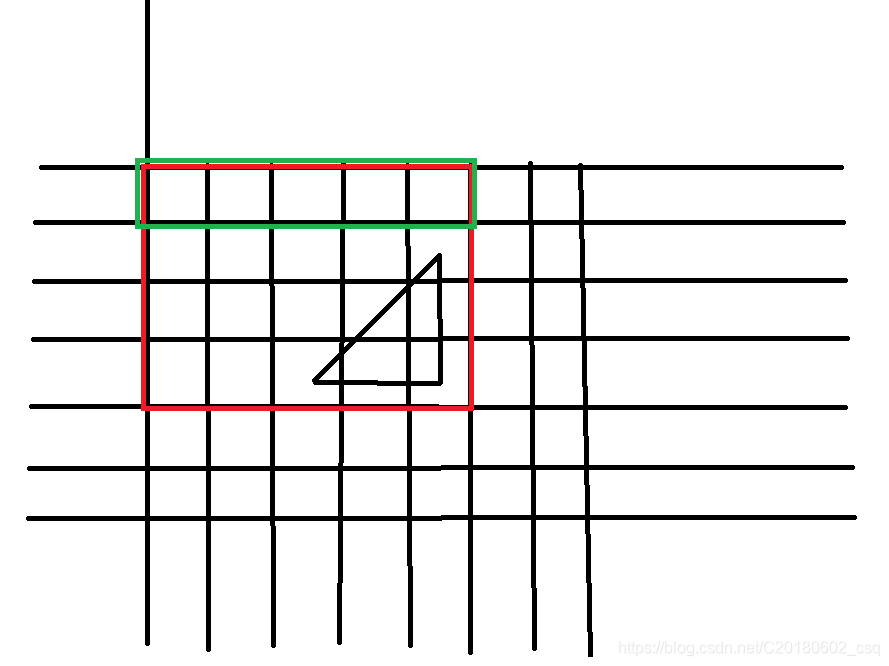
首先我们可以维护一个矩形的前缀和
(红色表示加,绿色表示减)
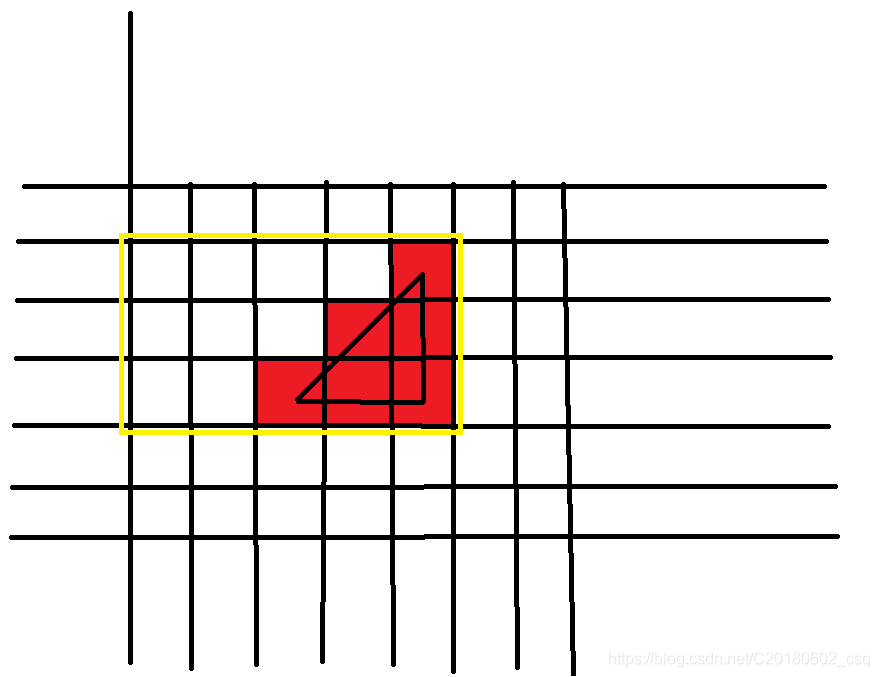
我们就可以算出黄色方框里的和
比红色的面积还多了一点
想办法减掉那个多出来的梯形
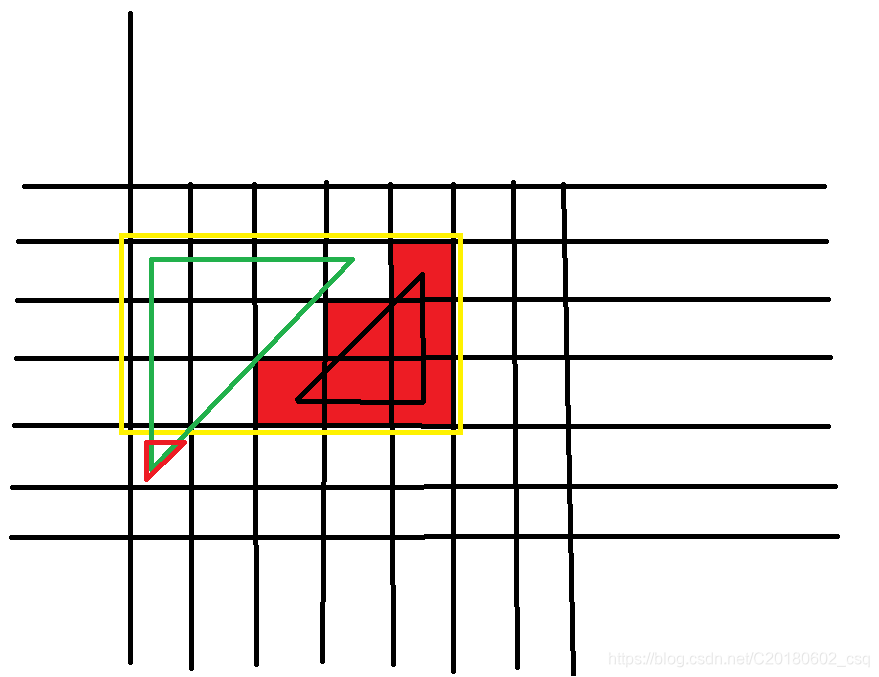
于是我们可以维护一个三角形的前缀和(用两个三角形相减得一个梯形)
我们减掉一个绿色的三角形发现减多了,又加上一个红色的小三角形
所以总体思路是:(注意坐标)
我们只需要维护两种前缀和,在加加减减一下就可以搞出来啦
#include
#include
#include
using namespace std;
#define N 3005
unsigned int f[3000005];
unsigned int A,B,C;
inline unsigned int rng61()
{
A^=A<<16;
A^=A>>5;
A^=A<<1;
unsigned int t=A;
A=B;
B=C;
C^=t^A;
return C;
}
unsigned int a[N][N],sum[N][N];
int main()
{
freopen("triangle.in","r",stdin);
freopen("triangle.out","w",stdout);
int n,m,q,i,j,x,y,k;
scanf("%d%d%d%u%u%u", &n, &m, &q, &A, &B, &C);
for(i = 1; i<= n; i++)
for(j = 1; j <= m; j++){
a[i][j] = rng61()+a[i][j-1];
sum[i][j]=a[i][j];
}
for(j=1;j<=m;j++)
for(i=1;i<=n;i++){
a[i][j]+=a[i-1][j];
sum[i][j]+=sum[i+1][j-1];
}
for(i = 1; i<= q; i++){
x = rng61() % n + 1;
y = rng61() % m + 1;
k = rng61() % min(x, y) + 1;
f[i]=a[x][y]-a[x-k][y]-sum[x-k+1][y-1]+sum[x+1][max(y-k-1,0)];
}
unsigned int ans=0,tmp=1;
for(i=q;i>=1;i--){
ans+=f[i]*tmp;
tmp*=233u;
}
printf("%u",ans);
}
我竟然调了一个小时,结果发现 f 数组开小了。。。