morris算法实现二叉树遍历

在刷leetcode上二叉树相关题目时144题，看到了一种morris的实现方式，可以把实现的空间复杂度降低到O(1),解法研究半天也是一头雾水，网上找资料和视频详细学了一下。

题目：

 144.二叉树前序遍历

94. 二叉树的中序遍历

145. 二叉树的后序遍历

递归解法

对于前中后序遍历，常规的递归解题套路：

  public void preOrder(List res, TreeNode root) {
        if (root == null) return;

        res.add(root.val);//前序
        preOrder(res, root.left);
        res.add(root.val);//中序
        preOrder(res, root.right);
        res.add(root.val);//后序
    }

对于递归解法来说，会使用一个树身高度的额外空间存储从根节点到叶子节点的元素，用于回溯的时候找到父节点，所以时间复杂度和空间复杂度均为O(n)

morris算法实现

有一种巧妙的方法可以在线性时间内，只占用常数空间来实现前序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出，因此被称为 Morris 遍历。

左神的讲解就通俗易懂了，学习地址：左神讲解morris遍历

Morris 遍历的核心思想是利用树的大量空闲指针，实现空间开销的极限缩减。其规则总结如下：

1.定义当前节点为cur,初始化为根节点
2.如果当前节点cur无左子树，cur = cur.right，如果此时cur = null
3.如果当前节点cur有左子树，找到左子树的最最右侧的右子树，记为mostRight.  
  此时分两种情况：
    (1) 最右侧节点mostRight的右指针指向null, 即mostRight.right = null ,此时mostRight.right = cur, cur = cur.left; 
    (2)最右侧节点mostRight的有指针指向当前节点cur,说明是第二次访问到当前节点cur,此时设置 mostRight.right = null  ,cur = cur.right;
遍历停止的条件是cur = null

 通过的代码模板如下：

    public void morris(TreeNode root) {
        if (root == null) return ;

        TreeNode cur = root;//定义当前节点，初始化为root
        TreeNode mostRight = null;//定义左子树的最右节点
        while (cur != null) {
           mostRight = cur.left;
           if (mostRight != null) {//包含左子树
               //查找左子树最右节点，且cur不是第二次访问
               while (mostRight.right != null && mostRight.right != cur) {
                   mostRight = mostRight.right;
               }
               
               if (mostRight.right == null) {//cur为第一次访问
                   mostRight.right = cur;
//                   System.out.println(cur.val + " ");
                   cur = cur.left;
                   continue;
               } 
               else {//cur为第二次访问
                   mostRight.right = null;
                   cur = cur.right;
               }
           } else { //无左子树
//               System.out.println(cur.val + " ");
               cur = cur.right;
           }
        }
    }

由于遍历过程中仅仅使用了最右子树的空闲指针的指向当前节点，用于回溯，所以无额外空间开销，空间复杂度O(1)。

前序遍历morris实现：

    public List preorderTraversal(TreeNode root) {
        List res = new ArrayList<>();
        if (root == null) {
            return res;
        }

        morrisPre(root, res);
        return res;
    }

    public void morrisPre(TreeNode root, List res) {
        if (root == null) return ;

        TreeNode cur = root;//定义当前节点，初始化为root
        TreeNode mostRight = null;//定义左子树的最右节点
        while (cur != null) {
           mostRight = cur.left;
           if (mostRight != null) {//包含左子树
               //查找左子树最右节点，且cur不是第二次访问
               while (mostRight.right != null && mostRight.right != cur) {
                   mostRight = mostRight.right;
               }

               if (mostRight.right == null) {//cur为第一次访问
                   mostRight.right = cur;
                   res.add(cur.val);//包含左子树的情况，在访问左子树之前记录当前根节点
                   cur = cur.left;
                   continue;
               }
               else {//cur为第二次访问
                   mostRight.right = null;
                   cur = cur.right;
               }
           } else { //无左子树
               res.add(cur.val);//无左子树的情况，在访问右子树之前记录当前根节点
               cur = cur.right;
           }
        }
    }

总结：第一次访问到一个节点，马上进行保存，即为先序（morris,访问顺序是根左右）

中序遍历morris实现：

public List inorderTraversal(TreeNode root) {
        List res = new ArrayList<>();
        if (root == null) {
            return res;
        }

        morrisIn(root, res);
        return res;
    }

    public void morrisIn(TreeNode root, List res) {
        if (root == null) return ;

        TreeNode cur = root;//定义当前节点，初始化为root
        TreeNode mostRight = null;//定义左子树的最右节点
        while (cur != null) {
           mostRight = cur.left;
           if (mostRight != null) {//包含左子树
               //查找左子树最右节点，且cur不是第二次访问
               while (mostRight.right != null && mostRight.right != cur) {
                   mostRight = mostRight.right;
               }

               if (mostRight.right == null) {//cur为第一次访问
                   mostRight.right = cur;
                   cur = cur.left;
                   continue;
               }
               else {//cur为第二次访问
                   mostRight.right = null;
                   res.add(cur.val);//无左子树的情况，在访问右子树之前记录当前根节点
                   cur = cur.right;
               }
           } else { //无左子树
               res.add(cur.val);//无左子树的情况，在访问右子树之前记录当前根节点
               cur = cur.right;
           }
        }
    }

总结：有左子树的节点第二次访问到一个节点，马上进行保存，无左子树，访问右子树之前进行保存，简单来说就是只要一个节点要往右子树移动，就进行保存，即为中序（morris,访问顺序是根左右）

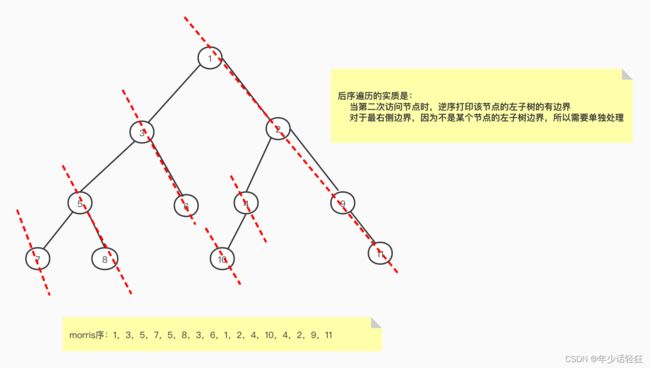
后序遍历morris实现：

    public List postorderTraversal(TreeNode root) {
        List res = new ArrayList<>();
        if (root == null) {
            return res;
        }

        morrisPost(root, res);
        return res;
    }

    public void morrisPost(TreeNode root, List res) {
        if (root == null) return ;

        TreeNode cur = root;//定义当前节点，初始化为root
        TreeNode mostRight = null;//定义左子树的最右节点
        while (cur != null) {
           mostRight = cur.left;
           if (mostRight != null) {//包含左子树
               //查找左子树最右节点，且cur不是第二次访问
               while (mostRight.right != null && mostRight.right != cur) {
                   mostRight = mostRight.right;
               }

               if (mostRight.right == null) {//cur为第一次访问
                   mostRight.right = cur;
                   cur = cur.left;
                   continue;
               }
               else {//cur为第二次访问
                   mostRight.right = null;
                   //逆序打印当前节点左子树的有边界
                   printEdge(cur.left, res);
                   cur = cur.right;  
               }
           } else { //无左子树
               cur = cur.right;
           }
        }
        //逆序打印从根节点开始的树的有边界
        printEdge(root, res);
    }

   public void printEdge(TreeNode head, List res) {
		TreeNode tail = reverseEdge(head);
		TreeNode cur = tail;
		while (cur != null) {
			res.add(cur.val);
			cur = cur.right;
		}
		// reverseEdge(tail);
	}

	public TreeNode reverseEdge(TreeNode root) {
		TreeNode pre = null;
		TreeNode cur = root;
		while (cur != null) {
			TreeNode next = cur.right;
			cur.right = pre;
			pre = cur;
			cur = next;
		}
		return pre;
	}

图解：