编译原理 期末复习

第二章 文法和语言

2.1 文法的直观概念

目前广泛使用的手段是上下文无关文法
语言研究的三个方面：语法、语义、语用
语法：记号的组合规律
语义：记号的特定含义
语用：记号行为的来源、使用、影响

2.2 符号和符号串

符号串集合的乘积，按笛卡尔乘积算
符号串的幂，代表数量
符号串集合的幂，也按笛卡尔乘积算，0次幂是空集
集合A的闭包是集合A的各次幂的∪，从0开始，记作A*
集合A的正闭包是集合A的各次幂的∪，从1开始，记作A⁺

2.3 文法和语言的形式定义

文法G定义为四元组（V_N,V_T,P,S):
V_N是非终结符集
V_T终结符集
P是规则集合
S是开始符

2.5 上下文无关文法及其语法树

语法树：从S开始推导
一个句型不只对应一棵语法树

2.6 句型的分析

自上而下分析法（画语法树从上往下画）
自下而上分析法（画语法树从下往上画，可能会回溯）
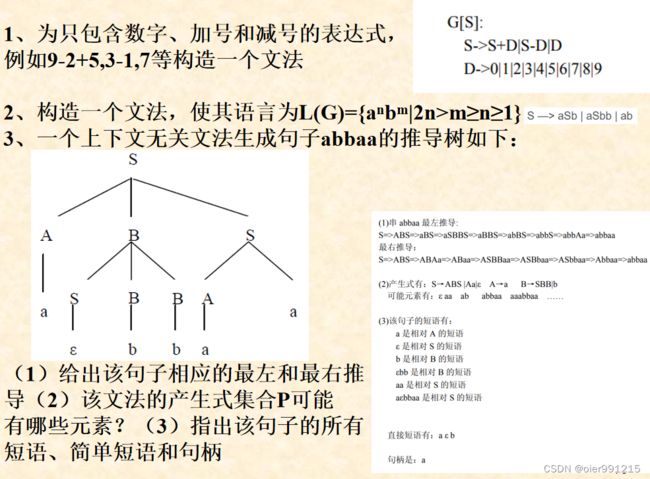
如果S (*)-> αβδ且 A(+)->β， 则称β是句型αβδ相对于非终结符A的短语。 特别，如有A->β则称β是句型αβδ相当于规则A->β的直接短语（也称简单短语）。
一个句型的最左直接短语成为该句型的句柄。
例子：

短语：语法树中任一子树叶节点所构成的符号串
直接短语：语法树中任意最小子树叶节点所构成的符号串
句柄：最左边的直接短语

2.7 有关文法实用中的一些说明（没看懂）

有害规则：U->U
多余规则：文法中一个句子的推导都用不到的规则

2.8 例题

1.写一文法，使其语言是奇数集合，但不允许出现以0打头的奇数。

ξ:N→A∣MA      /*一位数字│多位数字*/
M→B∣MD    /*仅两位数字(无中间位)│多于两位数字*/
A→1∣3∣5∣7∣9
B→1∣2∣3∣4∣5∣6∣7∣8∣9
D→0∣B

第三章 词法分析

3.2 单词的描述工具

正规式与正规集：
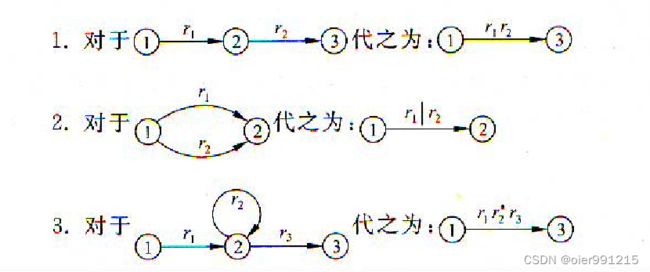
正规文法是不断做变换，直到每个表达式右端只含一个V_N(包含ε)

3.3 有穷自动机

3.3.1 确定的有穷自动机(DFA)(有限自动机)

DFA：能准确地识别正规集
一个确定的DFA：M=（K,∑,f,S,Z）
K是一个有穷集，每个元素成为一个状态
∑是一个有穷字母表，它的每个元素成为一个输入符号
f是转换函数，是在K×∑->K的映射。如果f(ki,a)=kj，(ki∈K，kj∈K）就意味着，当前状态为ki，输入符为a时，转换为下一个状态kj，我们把kj称作ki的一个后继状态
S是唯一一个初态，是一个元素
Z是一个终态集合，是集合

---

一个DFA可以表示一个状态图
构成：初态结点（要用→指出来）：，—； 终态结点（双圈，+），然后转换函数对应一条弧

---

一个DFA可以表示成一个矩阵
行表示状态，第一行默认为初态；列表示输入符号(a,b)，还要额外扩充一列，0表示非终态，1表示终态

---

这个意味着输入符号可以连续输入，对于状态S可以依次进行处理和变换，例如以下例题：

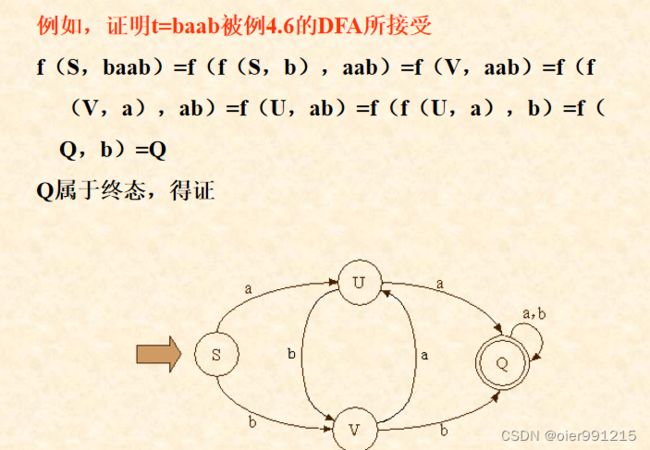
DFA可以确定转换函数唯一确定下一个状态

---

3.3.2 不确定的有穷自动机NFA

一个NFA：M=(K,∑,f,S,Z)
K是一个有穷集，每个元素成为一个状态
∑是一个有穷字母表，它的每个元素成为一个输入符号
f是转换函数，是在K×∑->K的映射。如果f(ki,a)=kj，(ki∈K，kj∈K）就意味着，当前状态为ki，输入符为a时，转换为下一个状态kj，我们把kj称作ki的一个后继状态
S是唯一一个初态，是一个元素
Z是一个终态集合，是集合

DFA是NFA的子集，可以用子集法转换

---

3.3.3 NFA转换为等价DFA

状态集合I的几个有关计算
1.ε-closure(I)：任何状态S经任意条ε弧而能到达的状态（元素）的集合（是包括本身的）。
2.move(I,a)：是可从I的某一状态经过一条a弧而到达的状态的全体（不包括本身）。

---

转换过程：
1.先求得T₀=ε-closure(初始状态S),添加到子集族C中
2.标记T₀，然后根据输入符号集进行bfs，将搜索到的（未被标记的）集合T_i添加到C中，继续遍历下一个T_i。重复2直到所有的T_i都被标记
3.记录T_i依次递推的关系（无论是否递推出了已被标记的集合）的状态。最终会获得T₁、T₂、T₃…然后重命名为 字母或数字，就可以画图得到DFA了

---

DFA的简化：
没有入度的点（非初态）应该删除

---

DFA最小化方法：

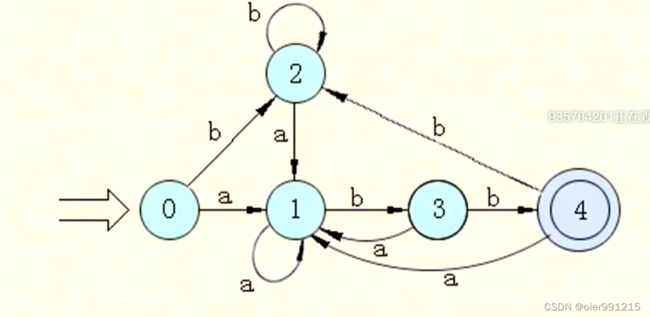
1.先分成终态集合和非终态集合
2.对每个集合中的符号分别用输出字母(a/b)去查看（不能识别的状态也单独划分）它们到达状态的集合是否在同一个集合中。如果不在同一个集合，将它们划分在不同的集合中，直到不能再划分为止（有点像并查集的逆过程）

3.4 正规式和有穷自动机的等价性

3.5 正规文法和有穷自动机的等价性

第三章保存一个例题：https://www.zhaokaoti.com/shiti/6793c604f0754d8e91db1bc4b79c207a.html

---

第四章 自顶向下语法分析方法

4.1 确定的自顶向下分析思想

求First集合：

第一种情况：A->a… ， a∈First(A)
第二种情况：A->B…，First(B)中的元素∈First(A)
第三种情况：First(ABC)的符号集：按照第二种情况拆分，如果A推导不出空串则减去空集后∪First(B)。。。B/C同理。

注意：First集合中的符号一定是终结符，也注意别漏下空串ε

求Follow集合：

注意：终结符的Follow集合没有定义，只有非终结符才会有Follow集合，同时Follow集合不包括空串ε。
开始符号的Follow里一定有#

第一种情况：A->…Ua 显然a∈Follow(U)
第二种情况：A->…UP 显然First§中的元素∈Follow(U)； 如果P可以推导出空集或P不存在，则Follow(A)中的元素也属于Follow(U).

求Select集合：

A->X,
如果X推导不出空串，则：Select(A->X) = First(X)
否则Select(A->X) = First(X)-ε+Follow(A)

参考资料

对每个非终结符A的两个不同产生式，满足Select(A->α)∩Select(A->β)=空集，则这是一个上下文无关文法。

4.3 某些非LL(1)文法到LL（1）文法的等价变换

1.提取左公共因子（可能要引入非终结符A’，用来去括号）
2.消除左递归（直接左递归和间接左递归）
1）直接左递归：消除直接左递归，改成右递归
2）用产生式去替换，变为直接左递归
3.消除文法中一切左递归的算法（没看）

4.4 不确定的自顶向下分析思想

1.由于相同左部产生式的右部FIRST集交集不为空而引起回溯
2.由于相同左部非终结符的右部存在能ε的产生式，且该非终结符的FOLLOW集中含有其他产生式右部FIRST集的元素
3.由于文法含有左递归而引起回溯

4.5 确定的自顶向下分析方法

1.递归子程序法
2.预测分析方法
预测分析表（一个矩阵，第一列是非终结符，第一行是终结符，矩阵填的内容是 →+右推导式）

判断是不是语句（示例，注意第一列为栈存放的顺序）

4.6 第四章习题

第五章 自底向上优先分析

5.1 自底向上优先分析

按照栈的顺序，将输入符号依次放入栈中，边移入边分析，产生句柄和规约串时进行替换(规约)

5.2 简单优先分析法

X=Y：A→…XY…
X X>Y：A→…BD…，且B+→…X(X是尾)和D*→Y…(Y是首)

例题：



可以把关系化成矩阵

---

简单优先文法的定义：
1.两个符号之间最多一种优先关系
2.两个产生式不会产生相同的右部

---

5.3 算符优先分析法

方法：把输入串的每个字符依次放入栈中，当栈里的元素可以规约时进行规约（看ppt看出来的方法）

---

算符优先关系表的构造（注意+→是可以多次推导的）：
Firstvt(B)的构成： B+→b…或B+→Cb…中的b（开头的b）
Lastvt(B)的构成：B+→…b或B+→…bC中的b（结尾的b）
应用：
=关系：A→aBc，a=c
<关系：A→…aB…，a >关系：A→…Ba…，Lastvt(B)中的元素>a
例题：




最左素短语：至少包含一个终结符，不包含其他素短语（最左边的）。

---

优先函数：f(a) g(b),a、b都是终结符，初始值全为1；然后扫描矩阵，进行递推，高运算函数=低运算函数+1；相同则更新min的一方=max的一方； 一直更新迭代直到无变化为止

---

关系图法构造优先函数
1.对所有终结符a用有下角标的 $f_a$、$g_a$为结点名。
2.若$a_i>a_k$或$a_i=a_k$，则从$f_{ai}$到$g_{ak}$画一条箭弧（高向低）
若$a_i<a_k$或$a_i=a_k$，则从$g_{ak}$到$f_{ai}$画一条箭弧（高向低）
3.给每个结点赋一个数，数值为从该节点出发所能到达的电的个数（包括该节点自身在内）；
4.与优先关系矩阵检查一遍是否还有满足优先关系的条件；

---

本章需要会做下面这个题

第六章 LR分析

6.1 LR分析概述

6.2 LR(0)分析表的构造

构造LR(0)分析表的方法：写出G的拓广文法G’，求出LR(0)项目集规范族C，构造识别文法全部活前缀的DFA，构造LR(0)分析表；
方法：

SLR(1)构造方法：

就是比LR(0)里少了点东西，少的东西是 $r_i$所在行，看$r_i$对应的产生式的左边（假设为E），那么这一行只填单列∈Follow(E)的空，其他空空着不填。