Python 模块之heapq
1、heapq介绍:
1)堆是非线性的树形的数据结构,有两种堆,最大堆与最小堆。( heapq库中的堆默认是最小堆)
- 最大堆,树种各个父节点的值总是大于或等于任何一个子节点的值。
- 最小堆,树种各个父节点的值总是小于或等于任何一个子节点的值。
2)堆是一个二叉树,其中最小堆每个父节点的值都小于或等于其所有子节点的值。整个最小堆的最小元素总是位于二叉树的根节点。
3)堆是用数组实现的二叉树,所以它没有使用父指针或者子指针。堆根据“堆属性”来排序,“堆属性”决定了树中节点的位置。
4)python的heapq模块提供了对堆的支持。 heapq堆数据结构最重要的特征是heap[0]永远是最小的元素
更多知识参考:数据结构:堆(Heap)
2、堆属性
1)例子:
这是一个最大堆,,因为每一个父节点的值都比其子节点要大。10 比 7 和 2 都大。7 比 5 和 1都大。
根据这一属性,那么最大堆总是将其中的最大值存放在树的根节点。而对于最小堆,根节点中的元素总是树中的最小值。堆属性非常有用,因为堆常常被当做优先队列使用,因为可以快速地访问到“最重要”的元素。
注意:堆的根节点中存放的是最大或者最小元素,但是其他节点的排序顺序是未知的。例如,在一个最大堆中,最大的那一个元素总是位于 index 0 的位置,但是最小的元素则未必是最后一个元素。--唯一能够保证的是最小的元素是一个叶节点,但是不确定是哪一个。
3、来自数组的树
用数组来实现树相关的数据结构也许看起来有点古怪,但是它在时间和空间上都是很高效的。
我们准备将上面例子中的树这样存储:
[ 10, 7, 2, 5, 1 ]
就这么多!我们除了一个简单的数组以外,不需要任何额外的空间。
如果我们不允许使用指针,那么我们怎么知道哪一个节点是父节点,哪一个节点是它的子节点呢?问得好!节点在数组中的位置index 和它的父节点以及子节点的索引之间有一个映射关系。
如果 i 是节点的索引,那么下面的公式就给出了它的父节点和子节点在数组中的位置:
parent(i) = floor((i - 1)/2)
left(i) = 2i + 1
right(i) = 2i + 2注意 right(i) 就是简单的 left(i) + 1。左右节点总是处于相邻的位置。
我们将写公式放到前面的例子中验证一下。
| Node | Array index (i) |
Parent index | Left child | Right child |
|---|---|---|---|---|
| 10 | 0 | -1 | 1 | 2 |
| 7 | 1 | 0 | 3 | 4 |
| 2 | 2 | 0 | 5 | 6 |
| 5 | 3 | 1 | 7 | 8 |
| 1 | 4 | 1 | 9 | 10 |
注意:根节点
(10)没有父节点,因为-1不是一个有效的数组索引。同样,节点(2),(5)和(1)没有子节点,因为这些索引已经超过了数组的大小,所以我们在使用这些索引值的时候需要保证是有效的索引值。
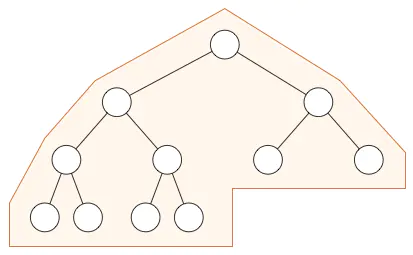
注意这个方案与一些限制。你可以在普通二叉树中按照下面的方式组织数据,但是在堆中不可以:
在堆中,在当前层级所有的节点都已经填满之前不允许开是下一层的填充,所以堆总是有这样的形状:
4、heapq方法介绍:
1)heappush(heap, item)
heapq.heappush(heap, item) 将item压入到堆数组heap中。如果不进行此步操作,后面的heappop()失效,会直接返回原列表第一个值,而且必须从头开始heappush,不然也会返回原列表第一个值。
例:
a = [12,2,4,5,63,3,2]
heapq.heappush(a,123)
>>>[12, 2, 4, 5, 63, 3, 2, 123]
b = heapq.heappop(a)
>>>122)heappop(heap)
删除并返回最小值,因为堆的特征是heap[0]永远是最小的元素,所以一般都是删除第一个元素。
注意,如果不是压入堆中,而是通过append追加一个数值,堆的函数并不能操作这个增加的数值,或者说它堆对来讲是不存在的。
例:
a = []
heapq.heappush(a,11)
heapq.heappush(a,2)
heapq.heappush(a,3)
heapq.heappush(a,4)
a.append(1)
b = heapq.heappop(a)
>>b=23)heapq.heapify(list)
参数必须是list,此函数将list变成堆,实时操作。从而能够在任何情况下使用堆的函数
例:
a = [12,2,4,5,63,3,2]
heapq.heapify(a)
heapq.heappop(a)4)heapq.heappushpop(heap, item)
是上述heappush和heappop的合体,同时完成两者的功能,注意:相当于先操作了heappush(heap,item),然后操作heappop(heap)5)heapq.heapreplace(heap, item)
是上述heappop和heappush的联合操作。注意:与heappushpop(heap,item)的区别在于,顺序不同,这里是先进行删除,后压入堆6)heapq.merge(*iterables)
将多个堆合并
a = [2, 4, 6]
b = [1, 3, 5]
c = heapq.merge(a, b)
>>[1, 2, 3, 4, 5, 6]7)heapq.nlargest(n, iterable,[ key])
查询堆中的最大n个元素8)heapq.nsmallest(n, iterable,[ key])
查询堆中的最小n个元素9)创建最大堆
heapq._heapify_max(queue)5、注意事项
当建堆的参数list的元素为tuple时,以tuple的第0个元素排序
例1:
S = "aab"
counts = collections.Counter(S).items()
heap = list(counts)
heapq._heapify_max(heap)
print(heap)输出结果为:
[('b', 1), ('a', 2)]
# 按字母的字典序进行排序
例2:
S = "aab"
counts = collections.Counter(S).items()
heap = [(x[1], x[0]) for x in counts]
heapq._heapify_max(heap)
print(heap)
[(2, 'a'), (1, 'b')]
# 按字母的出现顺序排序
参考文章:
数据结构:堆(Heap)
Python 模块之heapq