第六章 数理统计的基本概念
目录
- 一、基本概念
-
- 1.1 总体与个体(总体、个体、总体容量、总体分布、抽样、样本、样本容量、简单随机抽样的定义,简单随机样本的性质)
- 1.2 统计量与枢轴量(统计量、枢轴量、样本矩、样本矩的性质、二元总体的样本矩)
- 二、抽样分布(卡方分布、t分布、F分布的定义、上侧分位点与性质)
- 三、正态总体下的抽样分布(由一个正态总体的样本均值与样本方差构成的统计量的分布、由两个正态总体的样本均值与样本方差构成的统计量的分布)
说明:为了复习概率论,该文章是学习课程 《概率论与数理统计》教学视频全集(宋浩)而记录的笔记,笔记来源于本人,笔记包含的MATLAB代码来源于本人。若有侵权,请联系本人删除。笔记难免可能出现错误或笔误,若读者发现笔记有错误,欢迎在评论里批评指正。参考书籍: 《概率论与数理统计》_同济第五版_韩明、 《概率论与数理统计教程》_第三版 (茆诗松)、 《概率论与数理统计》_上交_徐晓岭。
一、基本概念
1.1 总体与个体(总体、个体、总体容量、总体分布、抽样、样本、样本容量、简单随机抽样的定义,简单随机样本的性质)
1.2 统计量与枢轴量(统计量、枢轴量、样本矩、样本矩的性质、二元总体的样本矩)
二、抽样分布(卡方分布、t分布、F分布的定义、上侧分位点与性质)
% 绘制卡方分布
clc;
clear ;
close all;
% 定义x轴范围
x = 0:0.1:20;
% 自由度参数数组
dof = [1, 2, 3, 4, 5, 6];
% 绘制概率密度图像
figure;
hold on;
for i = 1:length(dof)
% 计算卡方分布的概率密度函数
y = chi2pdf(x, dof(i));
% 绘制当前自由度的概率密度图像
plot(x, y, 'LineWidth', 1);
end
hold off;
grid on;
% 添加标题和轴标签
title('卡方分布概率密度函数图');
xlabel('x');
ylabel('概率密度 f_X');
% 添加图例
legend('自由度 = 1', '自由度 = 2', '自由度 = 3', '自由度 = 4', '自由度 = 5', '自由度 = 6');
% 绘制上测分位点
clc;
clear;
close all;
% 设置自由度和置信水平
dof = 4; % 自由度
alpha = 0.05; % 置信水平
% 计算上侧分位点
x = chi2inv(1 - alpha, dof);
% 输出结果
fprintf('卡方分布的上侧%0.2f分位点为 %.4f\n', alpha, x);
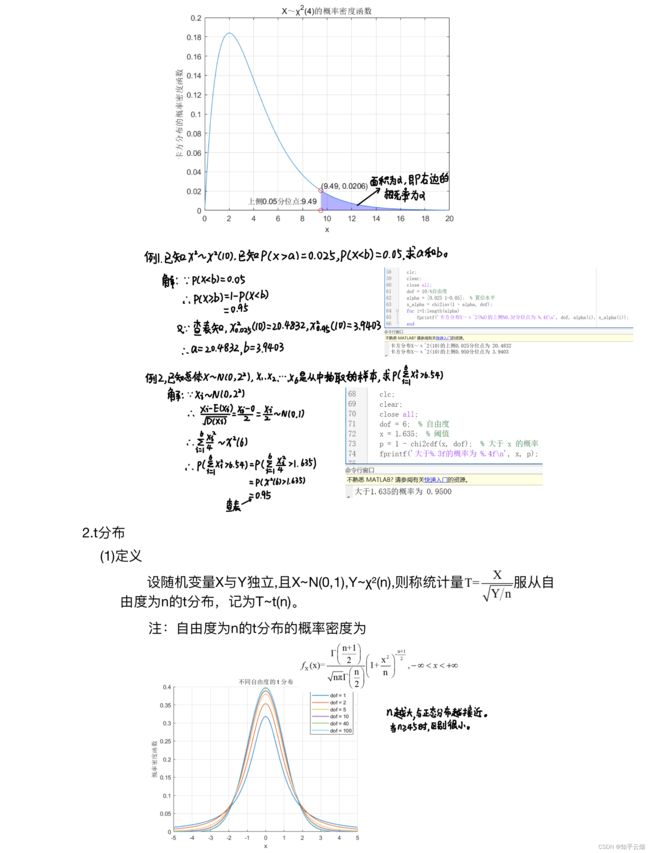
% 绘制卡方分布概率密度函数
x_values = 0:0.1:20;
y_values = chi2pdf(x_values, dof);
figure;
plot(x_values, y_values);
xlabel('x');
ylabel('卡方分布的概率密度函数');
title(sprintf('X~χ^2(%d)的概率密度函数', dof));
grid on;
% 标记上侧分位点
hold on;
plot(x, chi2pdf(x, dof), 'ro');
text(x, chi2pdf(x, dof), sprintf('(%.2f, %.4f)', x, chi2pdf(x, dof)), 'VerticalAlignment', 'bottom');
plot(x, 0, 'ro');
text(x-6, 0+0.01, sprintf('上侧%0.2f分位点:%0.2f', alpha, x));
% 添加阴影
x_area = x:0.1:20;
y_area = chi2pdf(x_area, dof);
area(x_area, y_area, 'FaceColor', 'blue', 'EdgeColor', 'none', 'FaceAlpha', 0.3);
hold off;
例1的代码:
% 例1
clc;
clear;
close all;
dof = 10;%自由度
alpha = [0.025 1-0.05]; % 置信水平
x_alpha = chi2inv(1 - alpha, dof);
for i=1:length(alpha)
fprintf('卡方分布X~χ^2(%d)的上侧%0.3f分位点为 %.4f\n', dof, alpha(i), x_alpha(i));
end
例2的代码:
% 例2
clc;
clear;
close all;
dof = 6; % 自由度
x = 1.635; % 阈值
p = 1 - chi2cdf(x, dof); % 大于 x 的概率
fprintf('大于%.3f的概率为 %.4f\n', x, p);
t分布的代码:
% t分布
clc;
clear;
close all;
% 设置自由度参数
dof = [1,2,5,10,40,100]; % 自由度
% 绘制 t 分布图像
x = -5:0.1:5; % x 范围
figure;
hold on;
for i = 1:length(dof)
y = tpdf(x, dof(i)); % 计算 t 分布概率密度函数
plot(x, y, 'LineWidth', 1);
end
hold off;
% 添加图例和标签
legend(sprintf('dof = %d', dof(1)), sprintf('dof = %d', dof(2)), sprintf('dof = %d', dof(3)),...
sprintf('dof = %d', dof(4)), sprintf('dof = %d', dof(5)), sprintf('dof = %d', dof(6)));
xlabel('x');
ylabel('概率密度函数');
title('不同自由度的 t 分布');
grid on;
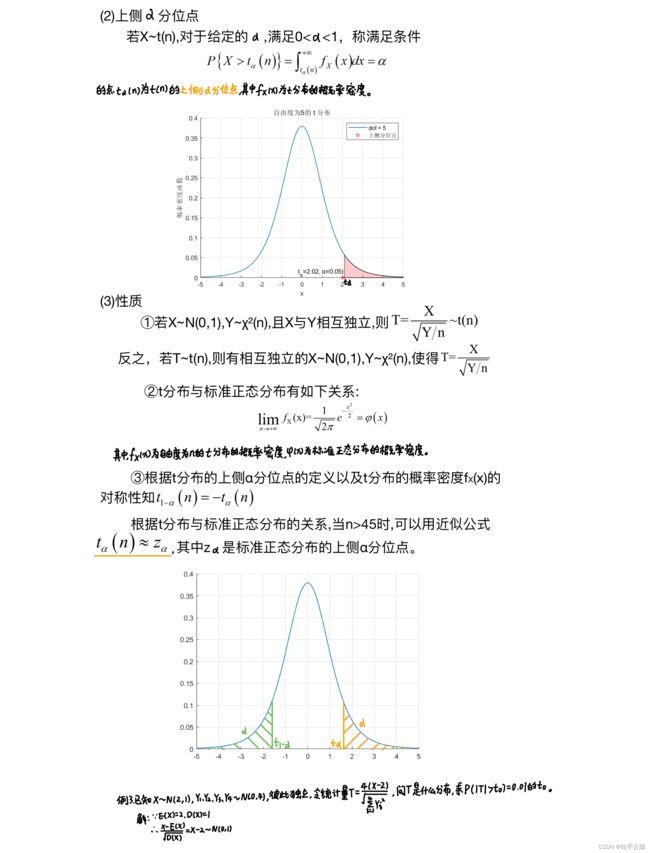
% t分布的上侧分位点
clc;
clear;
close all;
% 设置自由度参数
dof = 5; % 自由度
% 绘制 t 分布图像
x = -5:0.1:5; % x 范围
figure;
hold on;
y = tpdf(x, dof); % 计算 t 分布概率密度函数
plot(x, y, 'LineWidth', 1); % 画出t分布的概率密度函数
% 计算上侧分位点
p_upper = 0.05; % 上侧概率
t_value = tinv(1 - p_upper, dof); % 上侧分位点
y_max = max(y); % 最大概率密度值
% 绘制上侧分位点
plot(t_value, 0, 'ro', 'MarkerSize', 4, 'LineWidth', 1);
text(t_value - 2.2, 0, sprintf('t_α=%.2f, α=%.2f)', t_value, p_upper), ...
'VerticalAlignment', 'bottom', 'HorizontalAlignment', 'left');
% 添加阴影区域
x_fill = x(x > t_value); % 阴影区域x范围
y_fill = y(x > t_value); % 阴影区域y范围
fill([x_fill, fliplr(x_fill)], [y_fill, zeros(size(y_fill))], 'r', 'FaceAlpha', 0.2);
% 添加图例和标签
legend(sprintf('dof = %d', dof), '上侧分位点');
xlabel('x');
ylabel('概率密度函数');
title(sprintf('自由度为%d的 t 分布', dof));
grid on;
hold off;
% 例3
clc;
clear;
close all;
dof = 4; % 自由度
p_upper = 0.005; % 上侧分位点的概率
t_value = tinv(1 - p_upper, dof); % 上侧分位点
fprintf('t分布X~χ^2(%d)的上侧%0.3f分位点为 %.4f\n', dof, p_upper, t_value);
F分布的代码:
% F分布
clc;
clear;
close all;
% 设置自由度参数
dof1 = 3; % 分子自由度
dof2 = 5; % 分母自由度
% 绘制 F 分布图像
x = 0:0.01:6; % x 范围
y = fpdf(x, dof1, dof2); % 计算 F 分布概率密度函数
plot(x, y, 'LineWidth', 1); % 画出 F 分布的概率密度函数
% 添加图例和标签
legend(sprintf('F分布, (n_1 = %d, n_2 = %d)', dof1, dof2));
xlabel('x');
ylabel('概率密度函数');
title(sprintf('自由度为(%d,%d)的 F 分布', dof1, dof2));
grid on;
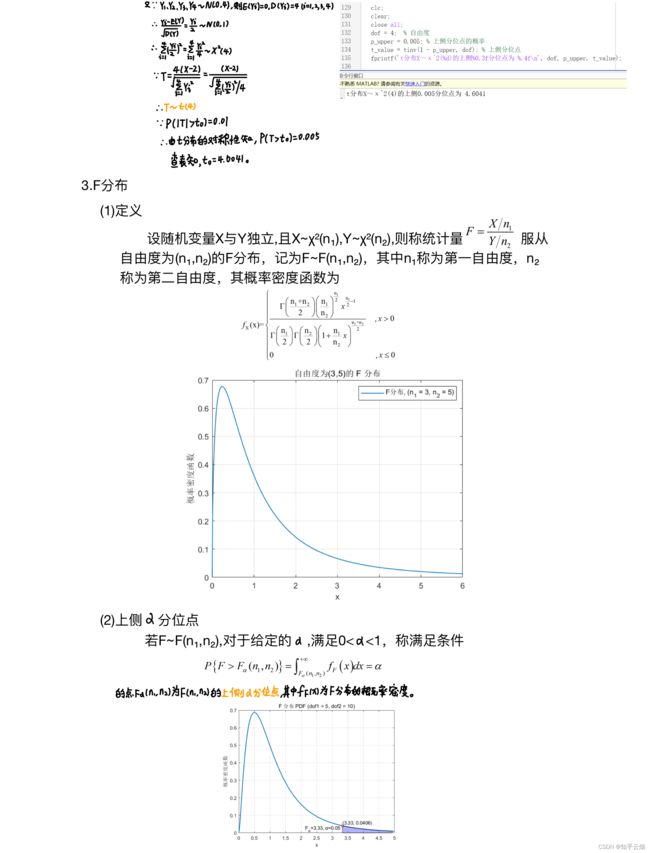
F分布的上侧分位点的代码:
% F分布的上侧分位点
clc;
clear;
close all;
% 设置自由度参数
dof1 = 5; % 分子自由度
dof2 = 10; % 分母自由度
alpha = 0.05; % 置信水平
% 计算上侧分位点
x = finv(1 - alpha, dof1, dof2);
% 绘制 F 分布概率密度函数
x_values = 0:0.01:5; % x 范围
y_values = pdf('F', x_values, dof1, dof2);
figure;
plot(x_values, y_values, 'LineWidth', 1.5);
xlabel('x');
ylabel('概率密度函数');
title(sprintf('F 分布 PDF (dof1 = %d, dof2 = %d)', dof1, dof2));
grid on;
% 标记上侧分位点
hold on;
plot(x, pdf('F', x, dof1, dof2), 'ro');
text(x, pdf('F', x, dof1, dof2), sprintf('(%.2f, %.4f)', x, pdf('F', x, dof1, dof2)), 'VerticalAlignment', 'bottom');
text(x-1.2, 0, sprintf('F_α=%.2f, α=%.2f', x, alpha), ...
'VerticalAlignment', 'bottom', 'HorizontalAlignment', 'left');
% 添加阴影
x_area = x:0.1:5;
y_area = pdf('F', x_area, dof1, dof2);
fill([x_area fliplr(x_area)], [y_area zeros(size(y_area))], 'b', 'FaceAlpha', 0.3);
hold off;
% 例5
clc;
clear;
close all;
% 设置自由度参数
dof1 = 10;
dof2 = 15;
alpha = 0.01; % 置信水平
x = finv(1 - alpha, dof1, dof2); % 计算上侧分位点
fprintf('F分布X~F^2(%d,%d)的上侧%0.3f分位点为λ1 = %.4f\n', dof1, dof2, alpha, x);
x = finv(1 - alpha, dof2, dof2); % 计算上侧分位点
fprintf('F分布X~F^2(%d,%d)的上侧%0.3f分位点为 %.4f\n', dof2, dof1, alpha, x);
fprintf('λ2 = %.4f\n',1/x);
三、正态总体下的抽样分布(由一个正态总体的样本均值与样本方差构成的统计量的分布、由两个正态总体的样本均值与样本方差构成的统计量的分布)
% 例1
clc;
clear;
close all;
p = 0.95;%大于上侧分位点的概率
v = 15;
x = tinv(1 - p, v);%求上侧分位点
fprintf('t分布X~t(%d)的上侧%0.3f分位点为 %.3f\n',v,p,x);
k = x/4;
fprintf('所求的k = %.3f\n', k);