力扣树专题-6 广度优先搜索 刷熟一个模板（层序遍历打印二叉树）秒杀一堆问题leetcode102 111 116 617 java刷题笔记

听不少大佬建议过——力扣刷题要从树开始 ！
因为可以建立起套路化的思路~ 另外就是锻炼好递归的思想
所以 我们从树开始~
本专题采用 前面提到的 “兔系刷题法”
不求钻研多种解法 只求快速见题型快速刷题！

另外 力扣评论区里看见的——

树的题目写不出来，多背几个模版就行。

前中后序、广度深度遍历、路径和、深度，直径，这些全部背下来。

感觉很有道理！多背些多理解些套路嘛！

本专题整理了tag中包括广度优先搜索的部分题型 都较为简单 适合初学者嗷

刷的这几道广度优先搜索都是使用迭代的方式对树进行一个遍历
都用到了一个队列对节点进行暂时存储
然后再将其按照顺序扔到结果列表中

关于这类题型
我认为可以使用一个模板
下面分享一下 也是我非常耐的一道题——剑指 Offer 32 - I 从上到下打印二叉树（其实就是层序遍历打印二叉树） 一个medium难度的easy题（挺好想的嗷~而且想明白了 刷熟练了套路就大体掌握了）
熟悉了这道题之后 可以解决好多题哦~
废话少说 快来解决这个层序遍历打印二叉树的题！！！

下面是两道模板题

剑指 Offer 32 - I. 从上到下打印二叉树 medium

我们的模板 一定要理解透 刷熟练它！

剑指 Offer 32 - I. 从上到下打印二叉树

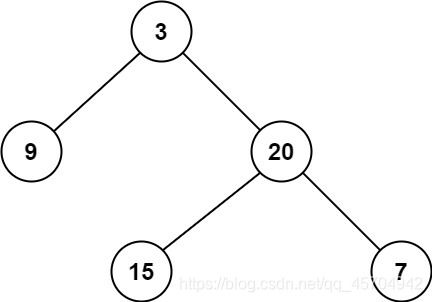
从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

例如:
给定二叉树: [3,9,20,null,null,15,7],

     3
	/ \
   9  20
   	 /  \
    15   7

返回：

[3,9,20,15,7]

解题思路

• 特例处理
• 初始化结果列表 和 包含所有根节点的队列
• 进行BFS循环 在队列 queue 为空时跳出
• • 队首元素出队并记为 node
  • 将 node.val添加到结果列表 tmp尾部
  • 向队列 queue中添加子节点（当前遍历到的 node节点的子节点）
• 将结果列表转换为结果数组来输出

用个循环就ok辽~

Java代码

迭代法

class Solution {
    public int[] levelOrder(TreeNode root) {
        // 01 特例处理
        if (root == null){
            return new int[0];
        }
        // 02 初始化队列 结果列表
        Queue<TreeNode> queue = new LinkedList<TreeNode>();//初始化队列 用于按顺序存放遍历到的每层的节点
        List<Integer> res = new ArrayList<Integer>();//初始化存结果的列表（但是这不是）
        queue.add(root);//先把根节点加到队列中————层序遍历第一个打印的节点

        //03 广度优先搜索
        while(!queue.isEmpty()){
            TreeNode node = queue.poll();//1 节点出队
            res.add(node.val);//将节点按顺序加入结果列表中
            if (node.left != null) queue.add(node.left);//如果下一层还有节点的话 将其入队
            if (node.right != null) queue.add(node.right);//下一层没节点的话 说明已经没有需要加入队列的节点了~
        }

        // 04 把列表转换成数组
        // 可以使用jdk8的新特性 stream流
        // return list.stream().mapToInt(Integer::intValue).toArray();
        // 但是上面这个速度会慢一些！
        int[] ans = new int[res.size()];//这个数组才符合输出条件~
        for (int i = 0; i <= res.size() - 1; i ++){
            ans[i] = res.get(i);//获取队列中的值 要使用.get(i) 
        } 
        return ans;
    }
}

102.二叉树的层序遍历

和上一题差不多意思~

102. 二叉树的层序遍历

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

输入：二叉树：[3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

输出：

[
  [3],
  [9,20],
  [15,7]
]

解题思路

在树的遍历中 使用了 BFS(Breadth-First-Search) 也就是广度优先搜索算法解决

【1】特例处理 判断边界条件——根为空

【2】初始化 创建 存放每层节点的队列queue 结果列表res

Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> res = new ArrayList();

别忘了根节点入队 queue.add(root);

【3】进行BFS广度优先搜索

{1}新建一个临时列表 用于存储当前层的打印结果

List<Integer> temp = new ArrayList<>();

{2}进行循环 把队列中的节点值 node.val 按序添加到临时列表temp的尾部 & 把加入列表节点的子节点加入到队列中

			for(int i = 0; i < levelNum; i++){
                //3 把队列中的元素加到临时列表中 
                TreeNode node = queue.poll();//节点入队
                temp.add(node.val);//加入当层结果中
     			// 4 结束每一个的元素的添加后 都要看一下它是否有下一层 
                // 如果有 就入到队列中排队去~
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
			//5 每层节点按序排好后加入到 结果二维数组 中
			res.add(temp);

【4】返回最终结果 二维数组 res ~

Java代码

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        //01 判断边界条件
        if(root == null){
            return new ArrayList<>();
        }
        //02 队列
        Queue<TreeNode> queue = new LinkedList<>();//存放每层的节点值
        List<List<Integer>> res = new ArrayList();//创建二维数组 结果
        //根节点入队
        queue.add(root);
        //03 进行BFS广度优先搜索
        while(!queue.isEmpty()){
            int levelNum = queue.size();//1 记录每层的节点数量
            List <Integer> temp = new ArrayList<>();//2 新建一个临时列表 存每层节点值
            for(int i = 0; i < levelNum; i++){
                //3 把队列中的元素加到临时列表中 
                TreeNode node = queue.poll();//节点出队
                temp.add(node.val);//加入当层结果中

                // 4 结束每一个的元素的添加后 都要看一下它是否有下一层 
                // 如果有 就入到队列中排队去~
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
            //5 每层节点按序排好后加入到 结果二维数组中
            res.add(temp);
        }
        // 04 BFS结束 输出最终结果
        return res;
    }
}

来做一些其他题强化下

111.二叉树的最小深度 easy

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

解题思路

【1】非递归 广度优先搜索

进行层序遍历 如果遍历到一个节点的左右子树同时为空 就返回最小深度

【2】递归

借鉴一位大佬的递归小技巧

• 写出结束条件
• 不要把树复杂化，就当做树是三个节点，根节点，左子节点，右子节点
• 只考虑当前做什么，不用考虑下次应该做什么
• 每次调用应该返回什么

Java代码

【1】非递归

class Solution {
    public int minDepth(TreeNode root) {
        if(root == null) return 0;
        int count = 0;//记录深度
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);

        while(!queue.isEmpty()){
            int size = queue.size();
            count += 1;
            for(int i = 0; i < size; i ++){
                //每一层的遍历 寻找是否有子节点
                TreeNode node = queue.poll();
                if (node.left == null && node.right == null){
                    return count;
                }
                if (node.left) {
                    queue.add(node.left);
                }
                if(node.right); {
                    queue.add(node.right);
                }
            }
        }
        return count;
    }
}

【2】递归

class Solution {
    public int minDepth(TreeNode root) {
        if(root == null) return 0;
        if (root.left == null && root.left == null) return 1;
        if (root.left!=null && root.right != null) return Math.min(minDepth(root.left), minDepth(root.right));
        if (root.left != null) return minDepth(root.left);//只考虑当前一层的状态~
        if (root.right != null) return minDepth(root.right);
    }
}

116.填充每个节点的下一个右侧节点指针 medium

116. 填充每个节点的下一个右侧节点指针

广度优先搜索

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例

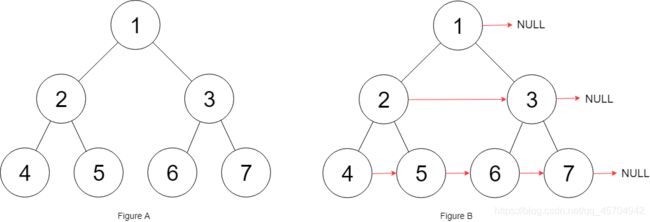
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

解题思路

参考题解 BFS解决（最好的击败了100%的用户）

要求把二叉树中每行都串联起来 那么最适合的就是BFS 也就是一行一行逐层进行的层序遍历~

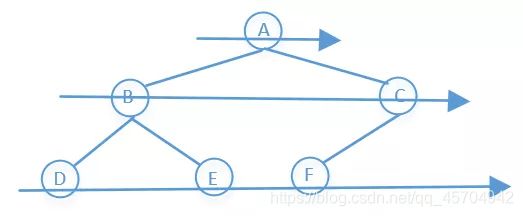
大佬给出了一幅图 很清晰~

在剑指 Offer 32 - I. 从上到下打印二叉树简单广度优先搜索算法的基础上 自然而然地引出了第一种方法

【1】使用队列

用队列将每一层串起来很简单

逐层遍历并进行串联 pre.next = node 即可

然而题目进阶要求是 —— 使用常数级的时间复杂度

【2】不使用队列

Java代码

【1】使用队列

class Solution {
    public Node connect(Node root) {
        if(root == null) return root;
        Queue<Node> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            int levelCount = queue.size();//每一层的节点数量
            Node pre = null;//前一个节点设置为空的
            for (int i = 0; i < levelCount; i ++){
                Node node = queue.poll();//将当前队列队头 进行出队 赋给node
                //如果pre不为空（为空的话代表node节点得到的值恰好是本层的第一个~）则让pre指向这个节点
                if(pre != null){
                    pre.next = node;
                }
                pre = node;//将遍历到的这个节点赋给pre 即 让这个节点成为“前一个节点”
                //遍历到的这个节点如果有子节点 就加入队列~
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
        }
        return root;
    }
}

N的时间复杂度

因为我们把节点不停的入队 然后再不停的出队

题目进阶要求 使用常数级的时间复杂度

【2】不使用队列

class Solution{
    public Node connect(Node root) {
        if (root == null)
            return root;
        //cur我们可以把它看做是每一层的链表
        Node cur = root;
        while (cur != null) {
            //遍历当前层的时候，为了方便操作在下一
            //层前面添加一个哑结点（注意这里是访问
            //当前层的节点，然后把下一层的节点串起来）
            Node dummy = new Node(0);
            //pre表示访下一层节点的前一个节点
            Node pre = dummy;
            //然后开始遍历当前层的链表
            while (cur != null) {
                if (cur.left != null) {
                    //如果当前节点的左子节点不为空，就让pre节点
                    //的next指向他，也就是把它串起来
                    pre.next = cur.left;
                    //然后再更新pre
                    pre = pre.next;
                }
                //同理参照左子树
                if (cur.right != null) {
                    pre.next = cur.right;
                    pre = pre.next;
                }
                //继续访问这一行的下一个节点
                cur = cur.next;
            }
            //把下一层串联成一个链表之后，让他赋值给cur，
            //后续继续循环，直到cur为空为止
            cur = dummy.next;
        }
        return root;
    }
}

117.填充每个节点的下一个右侧节点指针II medium

这题其实是个深度优先搜索
但是用层序遍历（广度）也可以做 就是空间复杂度不满足进阶要求（因为用了队列）

117. 填充每个节点的下一个右侧节点指针 II

给定一个二叉树（与116的区别就是不是完美二叉树 但是用广度优先搜索做的话 代码其实是一样的 反正都遍历一遍嘛~）

二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

解题思路和上一个一样哦

感觉和116也没有太大区别

就是本题如果再使用方法一会比较浪费空间（因为并不是所有节点都满足完美二叉树 排列得这么满）

具体的看上面116就可以

617.合并二叉树 easy

617. 合并二叉树

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。

你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

示例 1:

输入: 
Tree 1                     Tree 2                  
          1                         2                   
         / \                       / \                            
        3   2                     1   3                        
       /                           \   \                      
      5                             4   7 输出:            
合并后的树:
	     3
	    / \
	   4   5
	  / \   \ 
	 5   4   7	    	

解题思路

迭代方法

需要额外的数据结构来存储1 2号树的节点

可以借助栈和队列来完成

重点是广度优先搜索的逻辑

递归方法

相当于前序遍历嗷

重点同样是dfs的做法

递归方法单独写出来一个递归的dfs方法

其中递归的条件是这个方法的重点 搞明白了 就很容易地写出来了

代码逻辑

迭代方法

重点是广度优先搜索的逻辑 如下：

【1】

• 两棵树的左节点都不为null时 就放入队列中（其实用一个就行了 但是我用了两个。。有点蠢哈哈 但是比较直观嘛~）

• 右节点同理

【2】

不断地从队列中取出节点把它们相加

【3】

• 如果1号树的左节点为null 而2号树的左节点不为null 将2号树的左节点赋给1号树
• 右节点同理

【4】

最后返回root1

递归方法

递归的条件：

递归函数名称 dfs(TreeNode root1, TreeNode root2)

【1】终止条件：树1的节点为null 或者树2的节点为null

if(root1 == null || root2 == null){
	return root1 == null ? root2 : root1;
}

【2】递归函数内把两个数的节点相加后 赋给树1的节点

root1.val += root2.val;

【3】递归地执行两棵树的左节点 递归执行两棵树的右节点

root1.left = dfs(root1.left, root2.left);
root2.right = dfs(root2.left, root2.right);

【4】最终返回root1

Java代码

迭代方法

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1 == null){
            return root2;
        }
        if(root2 == null){
            return root1;
        }
        //这里其实创建一个队列就OK了~ 按顺序存两个树的节点
        Queue<TreeNode> queue1 = new LinkedList<>();//存左面树的节点
        Queue<TreeNode> queue2 = new LinkedList<>();
        queue1.add(root1);
        queue2.add(root2);
        //只要两个队列不都为空 就还没遍历到最后
        while(!queue1.isEmpty() || !queue2.isEmpty()){
            //进行广度优先搜索 一层一层地遍历 并将节点添加到
            TreeNode node1 = queue1.poll();
            TreeNode node2 = queue2.poll();
            //如果两个节点都在队列中
            node1.val += node2.val;
            //01 遍历到左边的子节点
            if (node1.left != null && node2.left != null) {
                //1、2号树对应节点如果都不为空 就加入到队列中 
                queue1.add(node1.left);
                queue2.add(node2.left);
            }
            else if (node1.left == null){
                //1号树对应节点如果为空 把2号树对应节点移过来
                node1.left = node2.left;
            }
            //02 右边的子节点同理
            if (node1.right != null && node2.right != null) {
                queue1.add(node1.right);
                queue2.add(node2.right);
            }
            else if (node1.right == null){
                node1.right = node2.right;
            }
        }
        return root1;
    }
}

递归方法

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null || root2 == null){
            return root1 == null ? root2:root1;
        }
        return dfs(root1, root2);
    }    
    public TreeNode dfs(TreeNode r1, TreeNode r2){
        //递归函数
       if(r1 == null || r2 == null){
           return r1 == null ? r2 : r1;
        }
        r1.val += r2.val;
        r1.left = dfs(r1.left,r2.left);
        r1.right = dfs(r1.right, r2.right);
        return r1;
    }
}