LeetCode--字符串

技巧

1.字符串是若干字符组成的有限序列，也可以理解为是一个字符数组。
2.双指针法在数组，链表和字符串中很常用。其实很多数组填充类的问题，都可以先预先给数组扩容带填充后的大小，然后在从后向前进行操作。
3.当需要固定规律一段一段去处理字符串的时候，要想想在在for循环的表达式上做做文章。
4.KMP。KMP的主要思想是当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。

题目

1.反转字符串
简单

思路：
双指针法。从头和末尾两个指针进行所指内容的交换。

/**
 * @param {character[]} s
 * @return {void} Do not return anything, modify s in-place instead.
 */
var reverseString = function(s) {
    let left = 0, right = s.length-1;
    while(left<right){
        [s[left],s[right]] = [s[right],s[left]];
        left++;
        right--;
    }
    return s;
};

2.反转字符串||
简单

思路：
双指针法。在遍历字符串的过程中，只要让 i += (2 * k)，i 每次移动 2 * k 就可以了，然后判断是否需要有反转的区间。

/**
 * @param {string} s
 * @param {number} k
 * @return {string}
 */
var reverseStr = function(s, k) {
    //split() 方法用于把一个字符串分割成字符串数组
    let arr = s.split('');
    let l = r =0;
    for(let i = 0;i<arr.length;i+=2*k){
        l=i;
        //注意i+k-1才是第k个元素下标
        if(i+k-1<arr.length){
             r = i+k-1;
        }
        else if(i+k-1>=arr.length){
             r = arr.length-1; 
        }
        while(l<r){
            [arr[l],arr[r]] = [arr[r],arr[l]];
            l++;
            r--;
            }

    }
    //join('')将数组元素无缝拼接 join(' ') 将数组元素以空格分割 join()将数组每个元素都转为字符串，用法等同于toString()
    return arr.join('')
};

3.替换空格
简单

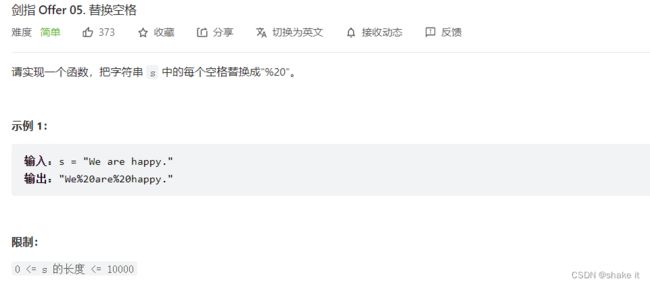
思路：
首先扩充数组到每个空格替换成"%20"之后的大小。然后从后向前替换空格，也就是双指针法。从前向后填充就是O(n^2)的算法了，因为每次添加元素都要将添加元素之后的所有元素向后移动。其实很多数组填充类的问题，都可以先预先给数组扩容带填充后的大小，然后在从后向前进行操作。

/**
 * @param {string} s
 * @return {string}
 */
var replaceSpace = function(s) {
    //转换为数组
    let arr = Array.from(s);
    //记录空格个数
    let count = 0;
    for(let i = 0;i<arr.length;i++){
        if(arr[i]==' ') count++;
    }
    //指向原数组末尾
    let oldArr = arr.length-1;
    //指向扩充后的数组末尾
    let newArr = arr.length-1+count*2;
    while(oldArr>=0){
        if(arr[oldArr]==' '){
            arr[newArr--] = '0';
            arr[newArr--] = '2';
            arr[newArr--] = '%';
            oldArr--;
        }
        else{
            arr[newArr--] = arr[oldArr--];
        }
    }
    return arr.join('');
};

4.反转字符串中的单词
中等

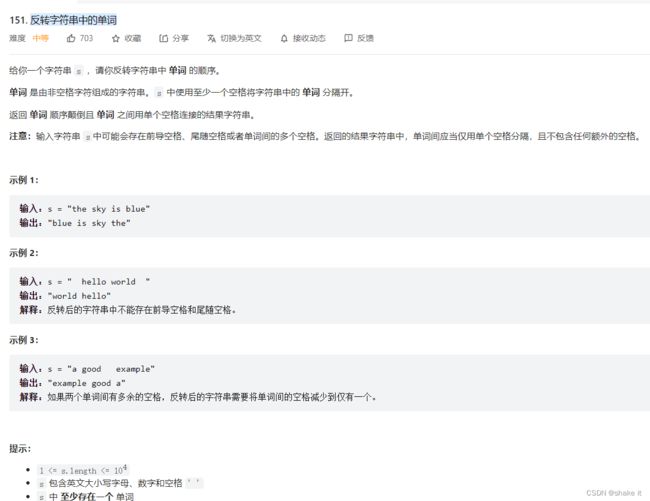
思路：
移除多余空格，将整个字符串反转，将每个单词反转。移除多余空格使用快慢指针。

/**
 * @param {string} s
 * @return {string}
 */
var deleteTab = function(a){
    let slow = fast = 0;
    for(let i = 0;i<a.length;i++){
        //删除开头和中间的多余空格
        if((i==0&&a[i]==' ')||(a[i]==' '&&a[i-1]==' ')){
            fast++;
        }
        else{
            a[slow++] = a[fast++];
        }
    }
    //循环结束slow==a.length(a是已经删除开头和中间多余空格后的数组，长度不同于一开始)
    //去除末尾空格
    a.length = slow;//超出新数组长度后的元素不考虑
    if(a[slow-1]==' ')a.length-=1;
    return a;
}
var reverse = function(a, start, end){
    while(start<end){
        [a[start],a[end]] = [a[end],a[start]];
        start++;
        end--;
    }
}
var reverseWords = function(s) {
    let arr = Array.from(s);
    //去除多余空格
    let a = deleteTab(arr);
    //反转整个数组
    reverse(a, 0, a.length-1);
    let left = 0;
    for(let i = 0; i<a.length; i++){
        if(a[i]==' '){
            reverse(a,left,i-1);
            left = i+1;
        }
        if(i==a.length-1){
            reverse(a,left,a.length-1)
        }
    }
    return a.join('');
};

5.左旋转字符串
简单

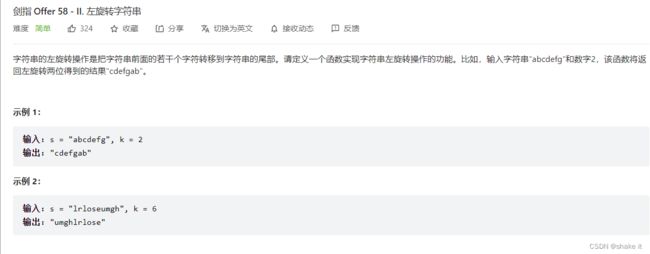
思路：
通过局部反转+整体反转 达到左旋转的目的。反转区间为前n的子串，反转区间为n到末尾的子串，反转整个字符串。

 * @param {string} s
 * @param {number} n
 * @return {string}
 */
var reverseLeftWords = function(s, n) {
    var reverse = function(a, start, end){
        while(start<end){
            [a[start], a[end]] = [a[end], a[start]];
            start++;
            end--;
        }
    }
    let a = Array.from(s);
    reverse(a, 0, n-1);
    reverse(a, n, a.length-1);
    reverse(a, 0, a.length-1);
    return a.join('');
};

6.实现 strStr()
中等

思路：
KMP算法。KMP的主要思想是当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。使用next数组记录了已经匹配的内容。
1.前缀表：前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。前缀表大小与模式串相同，记录下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。因为前缀表存的就是最长相等前后缀的长度。比如：
每次取相同长度的前后缀子串对比是否相同，存在就返回前后缀子串长度，不存在都是0.
a：前后缀都为0，长度为0；
aa：前后缀都为a，长度为1；
aab：前缀aa，后缀ab，不相同，再取前缀a，后缀b，不相同，长度为0；
aaba：前缀aab，后缀aba，不相同，再取前缀aa，后缀ba，不相同，再取前缀a，后缀a，相同，长度为1；
aabaa：前缀aaba，后缀abaa，不相同，再取前缀aab，后缀baa，不相同，再取前缀aa，后缀aa，相同，长度为2；
aabaaf：前缀aabaa，后缀abaaf，不相同，再取前缀aaba，后缀baaf，不相同，再取前缀aab，后缀aaf，不相同，再取前缀aa，后缀af，不相同，再取前缀a，后缀f，不相同，长度为0.
2.为什么要使用前缀表？

下标5之前这部分的字符串（也就是字符串aabaa）的最长相等的前缀 和 后缀字符串是 子字符串aa ，因为找到了最长相等的前缀和后缀，匹配失败的位置是后缀子串的后面，那么我们找到与其相同的前缀的后面重新匹配就可以了。匹配到模式串后缀的时候，说明文本串和模式串一样，有部分对称性。有对称性就说明：我前缀匹配的同时，与部分前缀相同的后缀同时也在匹配（这就节约了时间）。匹配到不正确的地方以前的子串跟上面的子串相等所以下面的子串的最长前缀肯定跟上面最长子串的后缀有匹配。
3.如何计算前缀表
前缀表大小与模式串相同，每个位置i记录标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。找到的不匹配的位置， 那么此时我们要看它的前一个字符的前缀表的数值是多少。因为要找前面字符串的最长相同的前缀和后缀。
4.构建next数组
有部分实现将前缀表统一减一（右移一位，初始位置为-1）之后作为next数组。这里我学的是让next数组就是前缀表。这两种只是具体实现的不同，不涉及原理。
5.时间复杂度
其中n为文本串长度，m为模式串长度，因为在匹配的过程中，根据前缀表不断调整匹配的位置，可以看出匹配的过程是O(n)，之前还要单独生成next数组，时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
6.踩坑
要先回退！！ 只要不相等就回退 保证有公共前后缀再判断下一步公共前后缀是否增加

/**
 * @param {string} haystack
 * @param {string} needle
 * @return {number}
 */
var strStr = function(haystack, needle) {
    var getNext = function(s){
        let next = new Array(s.length);
        //j表示最长公共前缀的末尾 也表示最长公共前后缀的长度（因为它等于最长公共前缀的长度）
        let j = 0;
        //只有一个字符的子串的最长公共前后缀为 0 
        next[0] = 0;
        //i表示最长公共后缀的末尾 对于任何一个到位置i(包括i)子串 最长后缀末尾都是本身 
        //如aab 最长前缀aa 最长后缀ab
        for(let i = 1; i<s.length; i++){
            //当不相等时 说明最长公共前后缀的长度不能增加了 那么就使用当前的前缀末尾之前的子串的最长公共长度
            //由于使用了j-1 保证j>0
            while(j>0&&s[i]!=s[j]){
                j = next[j-1];
            }
            //当两个末尾相等时 说明最长公共前后缀长度应该再加1
            if(s[i] == s[j]){
                j++;
            }
            //对于任何一个到位置i(包括i)子串 最长公共前缀长度也是最长公共前后缀长度
            next[i] = j;
        }
        return next;
    }
    let next = getNext(needle);
    //j指向模式串 i指向主串
    let j = 0;
    for(let i = 0; i<haystack.length;i++){
        //要先回退！！ 只要不相等就回退 保证有公共前后缀再判断下一步公共前后缀是否增加
        while(j>0&&haystack[i]!=needle[j]){
            j = next[j-1];
        }
        if(haystack[i] == needle[j])j++;
        //匹配成功 j大小为needle.length表示模式串已经全部匹配 此时i指向主串中模式串的最后一位
        if(j == needle.length) return (i-needle.length+1);
    }
    return -1;
};

7.重复的子字符串
简单

思路：
1.暴力解法。只需要判断，以第一个字母为开始的子串就可以。一个for循环获取子串的终止位置， 然后判断子串是否能重复构成字符串，又嵌套一个for循环，所以是O(n^2)的时间复杂度。遍历的时候 都不用遍历结束，只需要遍历到中间位置，因为子串结束位置大于中间位置的话，一定不能重复组成字符串。
2.移动匹配。字符串的结构一定是由前后相同的子串组成。既然前面有相同的子串，后面有相同的子串，用 s + s，这样组成的字符串中，后面s的前面的子串做后串，前面s的后面的子串做前串，就一定还能组成一个s。

判断字符串s是否由重复子串组成，只要两个s拼接在一起，里面还出现一个s的话，就说明是由重复子串组成。在判断 s + s 拼接的字符串里是否出现一个s的的时候，要刨除 s + s 的首字符和尾字符，这样避免在s+s中搜索出原来的s，我们要搜索的是中间拼接出来的s。
3.kmp解法。
在由重复子串组成的字符串中，最长相等前后缀不包含的子串就是最小重复子串。
这里拿字符串s：abababab 来举例，ab就是最小重复单位，如图所示：

步骤一：因为 这是相等的前缀和后缀，t[0] 与 k[0]相同， t[1] 与 k[1]相同，所以 s[0] 一定和 s[2]相同，s[1] 一定和 s[3]相同，即：，s[0]s[1]与s[2]s[3]相同 。
步骤二： 因为在同一个字符串位置，所以 t[2] 与 k[0]相同，t[3] 与 k[1]相同。
步骤三： 因为 这是相等的前缀和后缀，t[2] 与 k[2]相同 ，t[3]与k[3] 相同，所以，s[2]一定和s[4]相同，s[3]一定和s[5]相同，即：s[2]s[3] 与 s[4]s[5]相同。
步骤四：循环往复。
所以字符串s，s[0]s[1]与s[2]s[3]相同， s[2]s[3] 与 s[4]s[5]相同，s[4]s[5] 与 s[6]s[7] 相同。
正是因为 最长相等前后缀的规则，当一个字符串由重复子串组成的，最长相等前后缀不包含的子串就是最小重复子串。
假设字符串s使用多个重复子串构成（这个子串是最小重复单位），重复出现的子字符串长度是x，所以s是由n * x组成。
因为字符串s的最长相同前后缀的长度一定是不包含s本身，所以 最长相同前后缀长度必然是m * x，而且 n - m = 1，（这里如果不懂，看上面的推理）
所以如果 nx % (n - m)x = 0，就可以判定有重复出现的子字符串。
len为数组长度，如果len % (len - (next[len - 1] )) == 0 ，则说明数组的长度正好可以被 (数组长度-最长相等前后缀的长度) 整除 ，说明该字符串有重复的子字符串。
数组长度减去最长相同前后缀的长度相当于是第一个周期的长度，也就是一个周期的长度，如果这个周期可以被整除，就说明整个数组就是这个周期的循环。

/**
 * @param {string} s
 * @return {boolean}
 */
var repeatedSubstringPattern = function(s) {
    var getNext = function(s){
        let next = new Array(s.length);
        let j = 0;
        next[0] = j;
        for(let i = 1; i<s.length ;i++){
            //要先回退！！ 只要不相等就回退 保证有公共前后缀再进行下一步匹配 
            while(j>0&&s[i]!=s[j]){
                j = next[j-1];
            }
            if(s[i] == s[j]){
                j++;
            }
            next[i] = j;
        }
        return next;
    }
    let next = getNext(s);
    let len = next.length;
    if((next[len - 1]!=0) && (s.length % (s.length- next[len - 1]))==0)return true;
    return false;
};