求AOE中关键路径和关键活动(第七章 P183 算法7.13,7.14)
关键路径
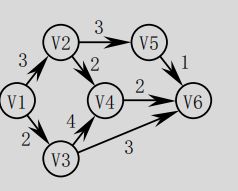
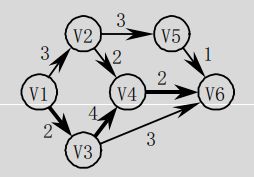
AOV网相对应的是AOE(Activity On Edge) ,是边表示活动的有向无环图,如下图所示。图中顶点表示事件(Event),每个事件表示在其前的所有活动已经完成,其后的活动可以开始;弧表示活动,弧上的权值表示相应活动所需的时间或费用。
与AOE有关的研究问题
◆ 完成整个工程至少需要多少时间?
◆ 哪些活动是影响工程进度(费用)的关键?
工程完成最短时间:从起点到终点的最长路径长度(路径上各活动持续时间之和) 。长度最长的路径称为关键路径,关键路径上的活动称为关键活动。关键活动是影响整个工程的关键。
设 v0 是起点,从 v0 到 vi 的最长路径长度称为事件 vi 的最早发生时间,即是以 vi 为尾的所有活动的最早发生时间。
若活动 ai 是弧
◆ e(i):表示活动 ai 的最早开始时间;
◆ l(i):在不影响进度的前提下,表示活动 ai 的最晚开始时间; 则 l(i)-e(i) 表示活动ai的时间余量,若 l(i)-e(i)=0,表示活动 ai 是关键活动。
◆ ve(i):表示事件 vi 的最早发生时间,即从起点到顶点 vi 的最长路径长度;
◆ vl(i):表示事件 vi 的最晚发生时间。则有以下关系:
含义是:源点事件的最早发生时间设为0;除源点外,只有进入顶点vj的所有弧所代表的活动全部结束后,事件 vj 才能发生。即只有 vj 的所有前驱事件 vi 的最早发生时间 ve(i) 计算出来后,才能计算 ve(j) 。
方法是:对所有事件进行拓扑排序,然后依次按拓扑顺序计算每个事件的最早发生时间。
含义是:只有 vj 的所有后继事件 vk 的最晚发生时间 vl(k) 计算出来后,才能计算 vl(j) 。
方法是:按拓扑排序的逆顺序,依次计算每个事件的最晚发生时间。
求AOE中关键路径和关键活动
算法思想
① 利用拓扑排序求出AOE网的一个拓扑序列;
② 从拓扑排序的序列的第一个顶点(源点)开始,按拓扑顺序依次计算每个事件的最早发生时间ve(i) ;
③ 从拓扑排序的序列的最后一个顶点(汇点)开始,按逆拓扑顺序依次计算每个事件的最晚发生时间vl(i) ;
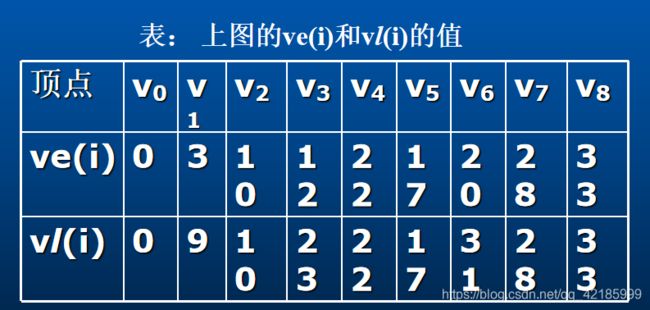
对于上图的AOE网,处理过程如下:
◆ 拓扑排序的序列是: (v0, v1, v2, v3 , v4, v5 , v6 , v7 , v8)
◆ 根据计算 ve(i) 的公式(2)和计算 vl(i) 的公式(3) ,计算各个事件的 ve(i) 和 vl(i) 值,如下表所示。
◆ 根据关键路径的定义,知该AOE网的关键路径是: (v0, v2, v4, v7 , v8) 和(v0, v2, v5 , v7 , v8) 。
◆ 关键路径活动是:
算法分析
设AOE网有n个事件,e个活动,则算法的主要执行是:
- ◆ 进行拓扑排序:时间复杂度是O(n+e) ;
- ◆ 求每个事件的 ve 值和 vl 值:时间复杂度是 O(n+e) ;
- ◆ 根据 ve 值和 vl 值找关键活动:时间复杂度是 O(n+e) ;
因此,整个算法的时间复杂度是O(n+e) 。
算法实现
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int Boolean; /* Boolean是布尔类型,其值是TRUE或FALSE */
#include /* malloc()等 */
#include /* EOF(=^Z或F6),NULL */
#include /* exit() */
#include //常量INT_MAX和INT_MIN分别表示最大、最小整数
/* 函数结果状态代码 */
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
#define MAX_NAME 5 /* 顶点字符串的最大长度+1 */
typedef int InfoType;
typedef char VertexType[MAX_NAME]; /* 字符串类型 */
/* --------------------------------- 图的邻接表存储表示 --------------------------------*/
#define MAX_VERTEX_NUM 20
typedef enum { DG, DN, AG, AN }GraphKind; /* {有向图,有向网,无向图,无向网} */
typedef struct ArcNode
{
int adjvex; /* 该弧所指向的顶点的位置 */
struct ArcNode *nextarc; /* 指向下一条弧的指针 */
InfoType *info; /* 网的权值指针) */
}ArcNode; /* 表结点 */
typedef struct
{
VertexType data; /* 顶点信息 */
ArcNode *firstarc; /* 第一个表结点的地址,指向第一条依附该顶点的弧的指针 */
}VNode, AdjList[MAX_VERTEX_NUM]; /* 头结点 */
typedef struct
{
AdjList vertices;
int vexnum, arcnum; /* 图的当前顶点数和弧数 */
int kind; /* 图的种类标志 */
}ALGraph;
/* ---------------------------------------------------------------------------------------------*/
/* ----------------------------- 需要用的图的邻接表存储的基本操作 --------------------------*/
int LocateVex(ALGraph G, VertexType u)
{ /* 初始条件: 图G存在,u和G中顶点有相同特征 */
/* 操作结果: 若G中存在顶点u,则返回该顶点在图中位置;否则返回-1 */
int i;
for (i = 0; i < G.vexnum; ++i)
if (strcmp(u, G.vertices[i].data) == 0)
return i;
return -1;
}
Status CreateGraph(ALGraph *G)
{ /* 采用邻接表存储结构,构造没有相关信息的图G(用一个函数构造4种图) */
int i, j, k;
int w; /* 权值 */
VertexType va, vb;
ArcNode *p;
printf("请输入图的类型(有向图:0,有向网:1,无向图:2,无向网:3): ");
scanf("%d", &(*G).kind);
printf("请输入图的顶点数,边数: ");
scanf("%d,%d", &(*G).vexnum, &(*G).arcnum);
printf("请输入%d个顶点的值(<%d个字符):\n", (*G).vexnum, MAX_NAME);
for (i = 0; i < (*G).vexnum; ++i) /* 构造顶点向量 */
{
scanf("%s", (*G).vertices[i].data);
(*G).vertices[i].firstarc = NULL;
}
if ((*G).kind == 1 || (*G).kind == 3) /* 网 */
printf("请顺序输入每条弧(边)的权值、弧尾和弧头(以空格作为间隔):\n");
else /* 图 */
printf("请顺序输入每条弧(边)的弧尾和弧头(以空格作为间隔):\n");
for (k = 0; k < (*G).arcnum; ++k) /* 构造表结点链表 */
{
if ((*G).kind == 1 || (*G).kind == 3) /* 网 */
scanf("%d%s%s", &w, va, vb);
else /* 图 */
scanf("%s%s", va, vb);
i = LocateVex(*G, va); /* 弧尾 */
j = LocateVex(*G, vb); /* 弧头 */
p = (ArcNode*)malloc(sizeof(ArcNode));
p->adjvex = j;
if ((*G).kind == 1 || (*G).kind == 3) /* 网 */
{
p->info = (int *)malloc(sizeof(int));
*(p->info) = w;
}
else
p->info = NULL; /* 图 */
p->nextarc = (*G).vertices[i].firstarc; /* 插在表头 */
(*G).vertices[i].firstarc = p;
if ((*G).kind >= 2) /* 无向图或网,产生第二个表结点 */
{
p = (ArcNode*)malloc(sizeof(ArcNode));
p->adjvex = i;
if ((*G).kind == 3) /* 无向网 */
{
p->info = (int*)malloc(sizeof(int));
*(p->info) = w;
}
else
p->info = NULL; /* 无向图 */
p->nextarc = (*G).vertices[j].firstarc; /* 插在表头 */
(*G).vertices[j].firstarc = p;
}
}
return OK;
}
Boolean visited[MAX_VERTEX_NUM]; /* 访问标志数组(全局量) */
void(*VisitFunc)(char* v); /* 函数变量(全局量) */
void Display(ALGraph G)
{ /* 输出图的邻接矩阵G */
int i;
ArcNode *p;
switch (G.kind)
{
case DG: printf("有向图\n");
break;
case DN: printf("有向网\n");
break;
case AG: printf("无向图\n");
break;
case AN: printf("无向网\n");
}
printf("%d个顶点:\n", G.vexnum);
for (i = 0; i < G.vexnum; ++i)
printf("%s ", G.vertices[i].data);
printf("\n%d条弧(边):\n", G.arcnum);
for (i = 0; i < G.vexnum; i++)
{
p = G.vertices[i].firstarc;
while (p)
{
if (G.kind <= 1) /* 有向 */
{
printf("%s→%s ", G.vertices[i].data, G.vertices[p->adjvex].data);
if (G.kind == DN) /* 网 */
printf(":%d ", *(p->info));
}
else /* 无向(避免输出两次) */
{
if (i < p->adjvex)
{
printf("%s-%s ", G.vertices[i].data, G.vertices[p->adjvex].data);
if (G.kind == AN) /* 网 */
printf(":%d ", *(p->info));
}
}
p = p->nextarc;
}
printf("\n");
}
}
/* --------------------------------------------------------------------------------------------------*/
/* 求关键路径。实现算法7.13、7.14的程序 */
int ve[MAX_VERTEX_NUM]; /* 全局变量(用于算法7.13和算法7.14) */
void FindInDegree(ALGraph G, int indegree[])
{ /* 求顶点的入度,算法7.13调用 */
int i;
ArcNode *p;
for (i = 0; i < G.vexnum; i++)
indegree[i] = 0; /* 赋初值 */
for (i = 0; i < G.vexnum; i++)
{
p = G.vertices[i].firstarc;
while (p)
{
indegree[p->adjvex]++;
p = p->nextarc;
}
}
}
typedef int SElemType; /* 栈类型 */
/* ----------------------------------- 栈的顺序存储表示 -----------------------------------*/
#define STACK_INIT_SIZE 10 /* 存储空间初始分配量 */
#define STACKINCREMENT 2 /* 存储空间分配增量 */
typedef struct SqStack
{
SElemType *base; /* 在栈构造之前和销毁之后,base的值为NULL */
SElemType *top; /* 栈顶指针 */
int stacksize; /* 当前已分配的存储空间,以元素为单位 */
}SqStack; /* 顺序栈 */
/* ---------------------------------------------------------------------------------------------*/
/* --------------------------------- 需要用到的顺序栈的基本操作 --------------------------------*/
Status InitStack(SqStack *S)
{ /* 构造一个空栈S */
(*S).base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));
if (!(*S).base)
exit(OVERFLOW); /* 存储分配失败 */
(*S).top = (*S).base;
(*S).stacksize = STACK_INIT_SIZE;
return OK;
}
Status StackEmpty(SqStack S)
{ /* 若栈S为空栈,则返回TRUE,否则返回FALSE */
if (S.top == S.base)
return TRUE;
else
return FALSE;
}
Status Push(SqStack *S, SElemType e)
{ /* 插入元素e为新的栈顶元素 */
if ((*S).top - (*S).base >= (*S).stacksize) /* 栈满,追加存储空间 */
{
(*S).base = (SElemType *)realloc((*S).base, ((*S).stacksize + STACKINCREMENT) * sizeof(SElemType));
if (!(*S).base)
exit(OVERFLOW); /* 存储分配失败 */
(*S).top = (*S).base + (*S).stacksize;
(*S).stacksize += STACKINCREMENT;
}
*((*S).top)++ = e;
return OK;
}
Status Pop(SqStack *S, SElemType *e)
{ /* 若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR */
if ((*S).top == (*S).base)
return ERROR;
*e = *--(*S).top;
return OK;
}
/* ---------------------------------------------------------------------------------------------*/
Status TopologicalOrder(ALGraph G, SqStack *T)
{ /* 算法7.13 有向网G采用邻接表存储结构,求各顶点事件的最早发生时间ve */
/* (全局变量)。T为拓扑序列顶点栈,S为零入度顶点栈。若G无回路,则用栈T */
/* 返回G的一个拓扑序列,且函数值为OK,否则为ERROR */
int j, k, count, indegree[MAX_VERTEX_NUM];
SqStack S;
ArcNode *p;
FindInDegree(G, indegree);/*对各顶点求入度indegree[0..vernum-1] */
InitStack(&S); /* 初始化栈 */
for (j = 0; j < G.vexnum; ++j) /* 建零入度顶点栈S */
if (!indegree[j])
Push(&S, j); /* 入度为0者进栈 */
InitStack(T); /* 初始化拓扑序列顶点栈 */
count = 0; /* 对输出顶点计数 */
for (j = 0; j < G.vexnum; ++j) /* 初始化ve[]=0 (最小值) */
ve[j] = 0;
while (!StackEmpty(S))
{ /* 栈不空 */
Pop(&S, &j);
Push(T, j); /* j号顶点入T栈并计数 */
++count;
for (p = G.vertices[j].firstarc; p; p = p->nextarc)
{ /* 对j号顶点的每个邻接点的入度减1 */
k = p->adjvex;
if (--indegree[k] == 0) /* 若入度减为0,则入栈 */
Push(&S, k);
if (ve[j] + *(p->info) > ve[k])
ve[k] = ve[j] + *(p->info);
}
}
if (count < G.vexnum)
{
printf("此有向网有回路\n");
return ERROR;
}
else
return OK;
}
Status CriticalPath(ALGraph G)
{ /* 算法7.14 G为有向网,输出G的各项关键活动 */
int vl[MAX_VERTEX_NUM];
SqStack T;
int i, j, k, ee, el;
ArcNode *p;
char dut, tag;
if (!TopologicalOrder(G, &T)) /* 产生有向环 */
return ERROR;
j = ve[0];
for (i = 1; i < G.vexnum; i++) /* j=Max(ve[]) 完成点的值 */
if (ve[i] > j)
j = ve[i];
for (i = 0; i < G.vexnum; i++) /* 初始化顶点事件的最迟发生时间(最大值) */
vl[i] = j; /* 完成点的最早发生时间 */
while (!StackEmpty(T)) /* 按拓扑逆序求各顶点的vl值 */
for (Pop(&T, &j), p = G.vertices[j].firstarc; p; p = p->nextarc)
{
k = p->adjvex;
dut = *(p->info); /* dut */
if (vl[k] - dut < vl[j])
vl[j] = vl[k] - dut;
}
printf(" j k dut ee el tag\n");
for (j = 0; j < G.vexnum; ++j) /* 求ee,el和关键活动 */
for (p = G.vertices[j].firstarc; p; p = p->nextarc)
{
k = p->adjvex;
dut = *(p->info);
ee = ve[j];
el = vl[k] - dut;
tag = (ee == el) ? '*' : ' ';
printf("%2d %2d %3d %3d %3d %c\n", j, k, dut, ee, el, tag); /* 输出关键活动 */
}
printf("关键活动为:\n");
for (j = 0; j < G.vexnum; ++j) /* 同上 */
for (p = G.vertices[j].firstarc; p; p = p->nextarc)
{
k = p->adjvex;
dut = *(p->info);
if (ve[j] == vl[k] - dut)
printf("%s→%s\n", G.vertices[j].data, G.vertices[k].data); /* 输出关键活动 */
}
return OK;
}
void main()
{
ALGraph h;
printf("请选择有向网\n");
CreateGraph(&h);
Display(h);
CriticalPath(h);
} 运行结果:
有向图:
关键路径: